Anomalia mimośrodowa
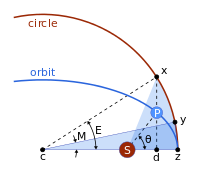
Anomalia mimośrodowa – parametr opisujący ruch ciała po orbicie keplerowskiej, zdefiniowany jako kąt pomiędzy odcinkiem łączącym geometryczny środek orbity z perycentrum a odcinkiem łączącym geometryczny środek orbity z punktem wyznaczonym przez przecięcie prostej prostopadłej do linii apsyd, przechodzącej przez ciało i okręgu opisanego na orbicie.
Anomalia mimośrodowa wiąże się z anomalią średnią przez równanie Keplera:
gdzie oznacza mimośród,
oraz z anomalią prawdziwą poprzez zależność:
Zobacz też[edytuj | edytuj kod]
Encyklopedia internetowa (wielkość fizyczna):








