B-drzewo

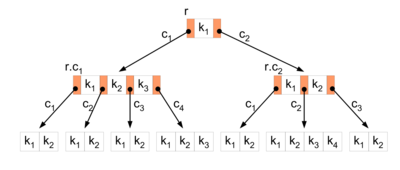
B-drzewo – drzewiasta struktura danych, przechowująca klucze w pewnym porządku i powiązane z nimi dane, używana przede wszystkim w systemach baz danych.

Głównym pomysłem zastosowanym w B-drzewach jest struktura wewnętrznego węzła. Każdy węzeł może posiadać od $M+1$ do $2\cdot M+1$ węzłów potomnych, gdzie $M$ to rząd B-drzewa; wyjątkiem jest korzeń, który może posiadać od $0$ do $2\cdot M+1$ węzłów potomnych. Te założenia gwarantują, że wysokość drzewa zawierającego $n$ kluczy będzie niska, rzędu $\log _{M}{n},$ co też powoduje, że asymptotyczna złożoność czasowa operacji podstawowych: wyszukiwania, wstawiania i kasowania kluczy jest rzędu $O(\log _{M}{n}).$

Niska wysokość drzewa powoduje, że liczba węzłów, które trzeba odczytać bądź zapisać, jest niewielka. W praktycznych zastosowaniach, w których informacje przechowywane są na dyskach twardych bądź płytach CD/DVD ma to fundamentalne znaczenie, bowiem czasy dostępu do tych urządzeń są dużo większe niż do pamięci wewnętrznej komputera i dominują w całkowitym czasie wykonywania operacji na danych (czasy dostępu do pamięci komputera rzędu mikro- lub setek nanosekund, natomiast do współczesnych dysków twardych to kilka milisekund – czyli 3–4 rzędy wielkości więcej). Z kolei zlokalizowanie odpowiedniego klucza bądź potomka w węźle wczytanym do pamięci wewnętrznej jest dużo szybsze, nawet jeśli rząd drzewa jest duży.

B+drzewo

Popularniejsze w zastosowaniach bazodanowych i systemach plików są B+drzewa, które są szczególnym przypadkiem B-drzew, przechowującym dane tylko w liściach.

Struktura węzła wewnętrznego

Każdy wewnętrzny węzeł drzewa posiada wartości rozdzielające (najczęściej są to po prostu stopnie wierzchołka), które wyznaczają jego poddrzewa. Przykładowo, jeśli węzeł wewnętrzny posiada 3 węzły (lub poddrzewa) potomne, to musi posiadać też 2 wartości rozdzielające A1 i A2. Wszystkie wartości mniejsze lub równe A1 znajdują się w poddrzewie po lewej stronie, wartości pomiędzy A1 i A2 znajdują się w środkowym poddrzewie, z kolei wartości większe od A2 są umiejscowione w prawym poddrzewie.

Każdej informacji w B-drzewie jest przyporządkowany unikatowy klucz względem którego całe drzewo zostało posortowane (dokładniej mówiąc to sortowanie odbywa się już w trakcie tworzenia drzewa, tak że od samego początku jest ono uporządkowane).

Każde B-drzewo jest rzędu M, tzn. każdy z węzłów zawiera od M do 2M kluczy (wyjątkiem jest korzeń, który może zawierać od 1 do 2M) i dlatego węzły są zawsze przynajmniej na wpół wypełnione kluczami. Węzeł posiadający k kluczy zawsze zawiera k+1 wskaźników (potomków – dzieci). Naprawdę duża liczba M (np. 1024) jest kluczowa w wydajności B-drzew, ponieważ wysokość drzewa dla ogromnej ilości węzłów liczonej w milionach lub miliardach będzie bardzo mała, np. dla M=1024 w B-drzewie o wysokości 2 można umieścić około miliona węzłów.

Zobacz też

• 2-3 drzewo
• drzewo binarne

Linki zewnętrzne

• Wizualizacja B-drzewa