Deterministyczny automat skończony (ang. Deterministic Finite-state Automaton , DFA ) to abstrakcyjna maszyna o skończonej liczbie stanów, która zaczynając w stanie początkowym czyta kolejne symbole pewnego słowa, po przeczytaniu każdego zmieniając swój stan na stan będący wartością funkcji jednego przeczytanego symbolu oraz stanu aktualnego. Jeśli po przeczytaniu całego słowa maszyna znajduje się w którymś ze stanów oznaczonych jako akceptujące (końcowe), słowo należy do języka regularnego , do rozpoznawania którego jest zbudowana.
Deterministyczny automat skończony, podobnie jak inne automaty skończone może być reprezentowany za pomocą tabeli przejść pomiędzy stanami lub diagramu stanów .
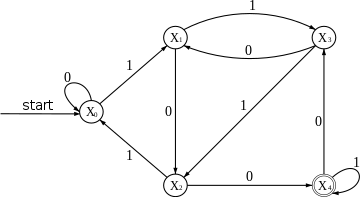
Zbudujmy na przykład maszynę rozpoznającą takie słowa nad alfabetem binarnym (reprezentujące liczby, przy najbardziej znaczącej z lewej strony), które są podzielne przez 5.
Żeby zbudować tę maszynę skorzystajmy z faktu, że:
w
⋅
0
=
2
w
,
{\displaystyle w\cdot 0=2w,}
w
⋅
1
=
2
w
+
1
{\displaystyle w\cdot 1=2w+1}
czyli:
c
n
⋅
c
n
−
1
…
c
1
⋅
c
0
=
c
0
+
2
(
c
1
+
2
(
…
(
c
n
−
1
+
2
(
c
n
)
)
…
)
)
.
{\displaystyle c_{n}\cdot c_{n-1}\dots c_{1}\cdot c_{0}=c_{0}+2(c_{1}+2(\dots (c_{n-1}+2(c_{n}))\dots )).}
Ale jako że obchodzi nas nie wynik, a jedynie jego podzielność przez 5, możemy wykonywać obliczenia w arytmetyce modulo 5.
Czyli zaczynamy od stanu
X
0
,
{\displaystyle X_{0},}
c
i
{\displaystyle c_{i}}
X
j
{\displaystyle X_{j}}
X
2
j
+
c
i
m
o
d
5
.
{\displaystyle X_{2j+c_{i}\,\mathrm {mod} \,5}.}
X
0
,
{\displaystyle X_{0},}
X
0
→
0
X
0
{\displaystyle X_{0}\to ^{0}X_{0}}
X
0
→
1
X
1
{\displaystyle X_{0}\to ^{1}X_{1}}
X
1
→
0
X
2
{\displaystyle X_{1}\to ^{0}X_{2}}
X
1
→
1
X
3
{\displaystyle X_{1}\to ^{1}X_{3}}
X
2
→
0
X
4
{\displaystyle X_{2}\to ^{0}X_{4}}
X
2
→
1
X
0
{\displaystyle X_{2}\to ^{1}X_{0}}
X
3
→
0
X
1
{\displaystyle X_{3}\to ^{0}X_{1}}
X
3
→
1
X
2
{\displaystyle X_{3}\to ^{1}X_{2}}
X
4
→
0
X
3
{\displaystyle X_{4}\to ^{0}X_{3}}
X
4
→
1
X
4
{\displaystyle X_{4}\to ^{1}X_{4}}
stan startowy –
X
0
{\displaystyle X_{0}}
stany akceptujące – tylko
X
4
.
{\displaystyle X_{4}.}
Deterministyczny automat skończony może zostać jednoznacznie opisany przez piątkę
(
A
,
Q
,
q
0
,
F
,
d
)
,
{\displaystyle (A,Q,q_{0},F,d),}
A
{\displaystyle A}
alfabetem wejściowym.
Q
{\displaystyle Q}
zbiorem stanów.
q
0
{\displaystyle q_{0}}
stanem początkowym należącym do
Q
.
{\displaystyle Q.}
F
{\displaystyle F}
stanów akceptujących (końcowych ), będącym podzbiorem
Q
.
{\displaystyle Q.}
d
{\displaystyle d}
funkcją przejścia , przypisującą parze
(
q
,
a
)
{\displaystyle (q,a)}
p
,
{\displaystyle p,}
a
{\displaystyle a}
q
.
{\displaystyle q.}
Funkcja
d
{\displaystyle d}
(
q
,
a
)
,
{\displaystyle (q,a),}
W powyższym przykładzie mamy:
A
=
{
0
,
1
}
{\displaystyle A=\{0,1\}}
Q
=
{
X
0
,
X
1
,
X
2
,
X
3
,
X
4
}
{\displaystyle Q=\{X_{0},X_{1},X_{2},X_{3},X_{4}\}}
q
0
=
X
0
{\displaystyle q_{0}=X_{0}}
F
=
{
X
0
}
{\displaystyle F=\{X_{0}\}}
d
:
{\displaystyle d{:}}
d
(
X
0
,
0
)
=
X
0
{\displaystyle d(X_{0},0)=X_{0}}
d
(
X
0
,
1
)
=
X
1
{\displaystyle d(X_{0},1)=X_{1}}
d
(
X
1
,
0
)
=
X
2
{\displaystyle d(X_{1},0)=X_{2}}
d
(
X
1
,
1
)
=
X
3
{\displaystyle d(X_{1},1)=X_{3}}
d
(
X
2
,
0
)
=
X
4
{\displaystyle d(X_{2},0)=X_{4}}
d
(
X
2
,
1
)
=
X
0
{\displaystyle d(X_{2},1)=X_{0}}
d
(
X
3
,
0
)
=
X
1
{\displaystyle d(X_{3},0)=X_{1}}
d
(
X
3
,
1
)
=
X
2
{\displaystyle d(X_{3},1)=X_{2}}
d
(
X
4
,
0
)
=
X
3
{\displaystyle d(X_{4},0)=X_{3}}
d
(
X
4
,
1
)
=
X
4
.
{\displaystyle d(X_{4},1)=X_{4}.}
Do każdego deterministycznego automatu skończonego istnieje jednoznaczny automat minimalny, który akceptuje ten sam język.
1. Usuń z automatu wszystkie stany, które nie są osiągalne ze stanu początkowego.
2. Utwórz tabelę par stanów automatu
{
X
i
,
X
j
}
,
{\displaystyle \{X_{i},X_{j}\},}
X
i
≠
X
j
.
{\displaystyle X_{i}\neq X_{j}.}
2.1. Zaznacz wszystkie pary stanów, gdzie
X
i
∈
F
,
{\displaystyle X_{i}\in F,}
X
j
∉
F
.
{\displaystyle X_{j}\notin F.}
2.2. Dla każdej nie zaznaczonej jeszcze pary stanów oraz dla każdego elementu
a
∈
A
{\displaystyle a\in A}
{
d
(
X
i
,
a
)
,
d
(
X
j
,
a
)
}
{\displaystyle \{d(X_{i},a),d(X_{j},a)\}}
{
X
i
,
X
j
}
.
{\displaystyle \{X_{i},X_{j}\}.}
2.3. Powtarzaj krok 2.2. tak długo, dopóki żadna zmiana w tabeli nie będzie już możliwa.
2.4. Każda para, która pozostała niezaznaczona, zostaje stopiona do jednego stanu. minimalizacja automatu rozpoznającego wyrazy binarne podzielne przez 5 (zobacz przykład automatu powyżej)
Krok 1: Wszystkie stany automatu są osiągalne ze stanu początkowego
X
0
.
{\displaystyle X_{0}.}
Krok 2: Tworzenie tabeli
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
X
3
{\displaystyle X_{3}}
X
4
{\displaystyle X_{4}}
X
0
{\displaystyle X_{0}}
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
X
3
{\displaystyle X_{3}}
Krok 2.1: Zaznaczamy wszystkie pary stanów, gdzie
X
i
∈
F
,
{\displaystyle X_{i}\in F,}
X
j
∉
F
.
{\displaystyle X_{j}\notin F.}
X
1
{\displaystyle X_{1}}
[0]
X
2
{\displaystyle X_{2}}
[0]
X
3
{\displaystyle X_{3}}
[0]
X
4
{\displaystyle X_{4}}
[0]
X
0
{\displaystyle X_{0}}
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
X
3
{\displaystyle X_{3}}
Kroki 2.2 – 2.3: Zaznaczamy parę
{
X
2
,
X
3
}
,
{\displaystyle \{X_{2},X_{3}\},}
d
(
X
2
,
1
)
=
X
0
{\displaystyle d(X_{2},1)=X_{0}}
d
(
X
3
,
1
)
=
X
2
,
{\displaystyle d(X_{3},1)=X_{2},}
{
X
0
,
X
2
}
{\displaystyle \{X_{0},X_{2}\}}
Zaznaczamy parę
{
X
1
,
X
2
}
,
{\displaystyle \{X_{1},X_{2}\},}
d
(
X
1
,
1
)
=
X
3
{\displaystyle d(X_{1},1)=X_{3}}
d
(
X
2
,
1
)
=
X
0
,
{\displaystyle d(X_{2},1)=X_{0},}
{
X
0
,
X
3
}
{\displaystyle \{X_{0},X_{3}\}}
Zaznaczamy parę
{
X
2
,
X
4
}
,
{\displaystyle \{X_{2},X_{4}\},}
d
(
X
2
,
1
)
=
X
0
{\displaystyle d(X_{2},1)=X_{0}}
d
(
X
4
,
1
)
=
X
4
,
{\displaystyle d(X_{4},1)=X_{4},}
{
X
0
,
X
4
}
{\displaystyle \{X_{0},X_{4}\}}
Zaznaczamy parę
{
X
1
,
X
3
}
,
{\displaystyle \{X_{1},X_{3}\},}
d
(
X
1
,
0
)
=
X
2
{\displaystyle d(X_{1},0)=X_{2}}
d
(
X
3
,
0
)
=
X
1
,
{\displaystyle d(X_{3},0)=X_{1},}
{
X
1
,
X
2
}
{\displaystyle \{X_{1},X_{2}\}}
Zaznaczamy parę
{
X
1
,
X
4
}
,
{\displaystyle \{X_{1},X_{4}\},}
d
(
X
1
,
0
)
=
X
2
{\displaystyle d(X_{1},0)=X_{2}}
d
(
X
4
,
0
)
=
X
3
,
{\displaystyle d(X_{4},0)=X_{3},}
{
X
2
,
X
3
}
{\displaystyle \{X_{2},X_{3}\}}
Zaznaczamy parę
{
X
3
,
X
4
}
,
{\displaystyle \{X_{3},X_{4}\},}
d
(
X
3
,
0
)
=
X
1
{\displaystyle d(X_{3},0)=X_{1}}
d
(
X
4
,
0
)
=
X
3
,
{\displaystyle d(X_{4},0)=X_{3},}
{
X
1
,
X
3
}
{\displaystyle \{X_{1},X_{3}\}}
X
1
{\displaystyle X_{1}}
[0]
X
2
{\displaystyle X_{2}}
[0]
[2]
X
3
{\displaystyle X_{3}}
[0]
[4]
[1]
X
4
{\displaystyle X_{4}}
[0]
[5]
[3]
[6]
X
0
{\displaystyle X_{0}}
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
X
3
{\displaystyle X_{3}}
Krok 2.4: Wszystkie pary stanów automatu zostały zaznaczone. Z tego wynika, że pierwotny automat jest już automatem minimalnym. Automater . fretka.porubis.pl. [zarchiwizowane z tego adresu (2010-09-01)].(pol. ) – demonstracja tworzenia minimalnego, deterministycznego automatu skończonego z podanego wyrażenia regularnego