Kąt wpisany

Kąt wpisany i kąt środkowy oparte na tym samym łuku

Kąt wpisany w okrąg – kąt, którego wierzchołek leży na okręgu, a ramiona zawierają cięciwy wychodzące z wierzchołka.

Np. kąt PQR pokazany na rysunku obok jest wpisany w okrąg. Mówimy, że kąt PQR jest oparty na łuku PR. Jeżeli kąt wpisany oparty jest na półokręgu, to mówimy również, że jest oparty na średnicy.

Z pojęciem kąta wpisanego związane jest pojęcie kąta środkowego.

Charakterystyka kąta wpisanego w okrąg

Twierdzenie o kącie środkowym i kącie wpisanym opartych na tym samym łuku

Miara kąta wpisanego jest dwa razy mniejsza od miary kąta środkowego opartego na tym samym łuku.

Dowód

Niech kąt wpisany ma miarę β, kąt środkowy oparty na tym samym łuku ma miarę α Poprowadźmy z wierzchołka kąta wpisanego promień (na ilustracji czerwony). Podzieli on ten kąt na dwa kąty o miarach $\beta =\beta _{1}+\beta _{2}$ i zarazem wyznaczy on dwa trójkąty równoramienne o kątach wierzchołkowych odpowiednio $\gamma _{1},\gamma _{2}.$ Dla obu tych równoramiennych trójkątów dostajemy zależności:

$2\cdot \beta _{1}+\gamma _{1}=\pi \quad (1)$

$2\cdot \beta _{2}+\gamma _{2}=\pi \quad (2)$

dodając stronami (1) i (2) oraz porządkując otrzymamy:

$2\cdot (\beta _{1}+\beta _{2})=2\pi -(\gamma _{1}+\gamma _{2})$

Ponieważ

$2\pi -(\gamma _{1}+\gamma _{2})=\alpha$

więc

$2\beta =\alpha$

Uwaga

Gdyby kąt środkowy nie mieścił się w odpowiadającym mu kącie wpisanym, to równości (1) i (2) należy odjąć zamiast dodać.

Gdyby wierzchołek kąta środkowego leżał na jednym z ramion kąta wpisanego to spośród równości (1) i (2) rozpatrujemy tylko jedną.

Wnioski

• Dowolny kąt wpisany oparty na półokręgu (czyli oparty na średnicy) jest kątem prostym, tzn. ma miarę 90°. Ten szczególny przypadek był już znany Talesowi.

• Dowolne dwa kąty wpisane oparte na tym samym łuku są równe, tzn. mają tę samą miarę.

Twierdzenie o kącie, którego ramiona przecinają okrąg

Jeśli wierzchołek kąta leży na zewnątrz okręgu, a oba jego ramiona mają punkty wspólne z tym okręgiem, to zachodzi jeden z trzech przypadków:

1. Oba ramiona są siecznymi okręgu, tzn. zawierają pewne cięciwy tego okręgu. Wtedy kąt wycina z okręgu dwa łuki rozłączne.
2. Jedno z ramion jest sieczną do okręgu, a drugie styczną. Wtedy kąt wycina z okręgu dwa łuki o jednym wspólnym końcu.
3. Oba ramiona są styczne do okręgu. Wtedy kąt dzieli okrąg na dwa komplementarne łuki o wspólnych wierzchołkach.

We wszystkich powyższych przypadkach jeden z wyznaczonych łuków jest położony bliżej wierzchołka kąta, a drugi dalej. Ten pierwszy nazwijmy łukiem bliższym, a drugi łukiem dalszym.

• 
  Kąt o obu ramionach siecznych do okręgu
• 
  Kąt o jednym ramieniu stycznym, a drugim siecznym do okręgu
• 
  Kąt o obu ramionach stycznych do okręgu

Twierdzenie 1

Jeśli wierzchołek kąta leży na zewnątrz okręgu, a oba jego ramiona mają punkty wspólne z tym okręgiem, to miara tego kąta jest równa połowie różnicy między kątem środkowym opartym na łuku dalszym a kątem środkowym opartym na łuku bliższym.

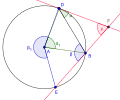
Dowód. Niech oba ramiona kąta $\gamma$ przecinają okrąg o środku A i promieniu r. Niech jedno ramię przecina okrąg w punktach C i D, a drugie w punktach B i D (jak na rysunku). Niech F będzie wierzchołkiem tego kąta, $\alpha _{1}=\angle BAD$ i $\beta _{1}=\angle CAE$ są kątami środkowymi opartymi na łukach BD i CE. Ponadto kąty $\alpha =\angle BCD$ oraz $\beta =\angle CBE$ są kątami wpisanymi opartymi odpowiednio na łukach BD i CE, czyli $\alpha =0,5\cdot \alpha _{1}$ i $\beta =0,5\cdot \beta _{1}.$ Z twierdzenia o kącie zewnętrznym wynika, że $\beta =\alpha +\gamma ,$ czyli

$\gamma =\beta -\alpha ={\frac {1}{2}}\cdot (\beta _{1}-\alpha _{1}),$

co kończy dowód w tym przypadku.

W pozostałych przypadkach (kąt o jednym ramieniu stycznym, a drugim siecznym oraz kąt o obu ramionach stycznych do okręgu) dowód jest taki sam. Wykorzystuje twierdzenie o kącie zewnętrznym trójkąta i łatwo go odtworzyć, posługując się poniższymi rysunkami.

Twierdzenie 2

Kąt o wierzchołku F wewnątrz okręgu

Jeśli wierzchołek kąta leży wewnątrz okręgu, to jego miara jest równa połowie sumy kątów środkowych opartych na łukach wyznaczonych przez ten kąt oraz przez kąt do niego wierzchołkowy.

Dowód. Ramiona kąta γ i ich przedłużenia przecinają okrąg odpowiednio w punktach C i E oraz D i B. Kąt γ jest kątem zewnętrznym trójkąta BCF, czyli jest równy sumie $\alpha +\beta .$ Natomiast kąty $\angle DCB=\alpha$ i $\angle CBE=\beta$ są kątami wpisanymi w okrąg, opartymi odpowiednio na łukach DB i CE i dlatego

$\gamma =\alpha +\beta =0,5\cdot (\alpha _{1}+\beta _{1}),$

co kończy dowód.

Wnioski

• Jeśli kąt jest oparty na łuku okręgu i nie jest kątem wpisanym w okrąg, to jego miara jest różna od połowy kąta środkowego opartego na tym samym łuku.
• Zbiór punktów, z których dany odcinek jest widziany pod określonym kątem jest łukiem pewnego okręgu.

Zobacz też

• kąt dopisany
• kąt środkowy