Manewr transferowy Hohmanna

Manewr transferowy Hohmanna – manewr ekonomicznej zmiany orbity kołowej statku kosmicznego na wyższą lub niższą, przez dwukrotne użycie silników. Statek wykonujący taki manewr porusza się po, tzw. orbicie transferowej Hohmanna.

Nazwa manewru

Nazwa pochodzi od nazwiska Waltera Hohmanna, niemieckiego naukowca, który opublikował założenia tego manewru w 1925. W literaturze radzieckiej i rosyjskiej używana jest również nazwa manewr transferowy Hohmanna-Wietczinkina. Drugie nazwisko pochodzi od radzieckiego matematyka, Władimira Petrowicza Wietczinkina, który zaprezentował ten manewr podczas swoich wykładów o podróżach międzyplanetarnych w latach 1921–1925.

Opis manewru

Manewr transferowy Hohmanna na wyższą orbitę

Podwyższanie orbity

Trajektoria lotu podczas manewru ma kształt połówki elipsy (2 na rysunku) stycznej zarówno do opuszczanej orbity kołowej (1 na rysunku), jak i do orbity docelowej (3 na rysunku). Elipsa ta jest nazywana orbitą transferową Hohmanna. Przejście z jednej orbity na drugą jest inicjowane poprzez pierwsze odpalenie silnika (ΔV na rysunku), co powoduje podwyższanie aktualnej orbity. Gdy statek dociera na wysokość orbity docelowej, następuje drugie odpalenie silnika (ΔV′ na rysunku). Ma ono na celu dostosowanie prędkości do prędkości orbitalnej wymaganej przez orbitę docelową i zmniejszenie jej mimośrodu. Obydwa impulsy nie muszą zostać wykonane podczas tego samego obiegu orbity – statek może przez pewien czas krążyć po orbicie transferowej.

Obniżanie orbity

Manewr transferowy Hohmanna pozwala także na sprowadzenie statku z wyższej orbity kołowej na niższą. W takim wypadku różnica leży jedynie w zwrocie wektora ciągu, siła ciągu musi zmniejszać prędkość statku. Spowolnienie lotu powoduje bowiem obniżenie orbity. Drugi impuls powoduje dostosowanie prędkości statku do prędkości wymaganej na nowej niższej orbicie i zmniejszenie jej mimośrodu.

Wpływ siły ciągu silników

Manewr Hohmanna przewiduje impulsową zmianę prędkości w celu nadania statkowi orbit kołowych, przeważnie więc używa się do niego silników o dużym ciągu (w celu minimalizacji ilości zużywanego paliwa). Silniki o małym ciągu mogą wykonać manewr Hohmanna w przybliżeniu, poprzez stopniowe powiększanie początkowej orbity. Wymaga to jednak delta-v do 141% większego niż przy wykorzystaniu dwóch silnych impulsów. Jest również bardziej czasochłonne.

Ekonomiczność

Manewr Hohmanna jest manewrem niemal zawsze najbardziej ekonomicznym, jeśli chodzi o zużycie paliwa. Jednym z przypadków, gdy tak nie jest, to gdy półoś wielka orbity docelowej jest ponad 12 razy większa niż półoś wielka orbity pierwotnej. Wtedy bardziej opłacalny staje się manewr dwueliptyczny.

Obliczenia

Bilans całkowitej energii mechanicznej przy przejściu Hohmanna z niższej orbity o promieniu wyjściowym $r_{p}$ do wyższej orbity o promieniu końcowym $r_{a}$

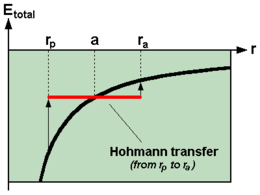
Całkowita Energia mechaniczna ciała o masie m okrążającego ciało o masie M jest sumą jego energii kinetycznej i potencjalnej, przy założeniu, że m jest zaniedbywalnie małe w porównaniu do M (czyli m << M), równa się połowie potencjału grawitacyjnego w najdalszym punkcie orbity ciała m – w odległości półosi wielkiej:

$E={\frac {1}{2}}mv^{2}-{\frac {GMm}{r}}={\frac {-GMm}{2a}}.$

Rozwiązując powyższe równanie można dojść do, tzw. równania zachowania energii orbitalnej:

$v^{2}=\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right),$

gdzie:

• $v$ – prędkość orbitującego ciała [m],
• $\mu =GM$ – tzw. standardowy parametr grawitacyjny ciała okrążanego (M),
• $r$ – odległość między ciałem orbitującym a okrążanym,
• $a$ – półoś wielka orbity ciała krążącego.

Zmiana prędkości wymagana do manewru Hohmanna wynosi:

$\Delta v_{P}={\sqrt {\frac {\mu }{r_{1}}}}\left({\sqrt {\frac {2r_{2}}{r_{1}+r_{2}}}}-1\right)$ ← dla impulsu w perycentrum elipsy łączącej obie orbity (początkową i docelową),

$\Delta v_{A}={\sqrt {\frac {\mu }{r_{2}}}}\left(1-{\sqrt {\frac {2r_{1}}{r_{1}+r_{2}}}}\,\!\right)$ ← dla impulsu w apocentrum tejże elipsy,

gdzie:

• $r_{1}$ – promień niższej orbity i odległość perycentrum orbity transferowej Hohmanna,
• $r_{2}$ – promień wyższej orbity i odległość apocentrum orbity transferowej Hohmanna.

Najmniejszy wymagany czas potrzebny na zmianę orbit (niezależnie w jakim kierunku: z niższej na wyższą czy z wyższej na niższą) określa trzecie prawo Keplera:

$t_{H}={\tfrac {1}{2}}{\sqrt {\frac {4\pi ^{2}a_{H}^{3}}{\mu }}}=\pi {\sqrt {\frac {(r_{1}+r_{2})^{3}}{8\mu }}},$

gdzie:

• $a_{H}$ – długość półosi wielkiej orbity transferowej Hohmanna.

Czas ten jest równy połowie okresu orbity transferowej.

Przykład

Dla orbity geostacjonarnej $r_{2}$ = 42 164 km; dla orbity o wysokości 300 km, $r_{1}$ = 6 678 km (odległość liczymy od wspólnego środka masy układu Ziemia – satelita, który leży niemalże w środku Ziemi).

Prędkość związana z orbitą większą wynosi 3,07 km/s, a z mniejszą, 7,73 km/s. Dla orbity eliptycznej (transferowej) waha się od 1,61 km/s w apogeum, do 10,15 km/s w perygeum.

Wymagane zmiany prędkości przy manewrze Hohmanna wyniosą więc:

• 3,07 – 1,61 = 1,46 km/s,
• 10,15 – 7,73 = 2,42 km/s.

Razem, 3,88 km/s.

Maksymalna wartość ΔV

Największa zmiana prędkości (delta-v) przy manewrze Hohmanna (53,6% pierwotnej prędkości orbitalnej) potrzebna jest, gdy promień orbity docelowej jest 15,6 razy większy od promienia orbity początkowej (rzeczywisty pierwiastek równania $x^{3}-15x^{2}-9x-1=0$). Dla wyższych orbit końcowych ΔV maleje i dąży do wartości prędkości początkowej razy ${\sqrt {2}}-1,$ czyli 41,4% pierwotnej prędkości orbitalnej.

Zmiana orbity wraz ze zmianą ciała centralnego

Użycie manewru Hohmanna przy zmianie orbity i jednoczesnej zmianie okrążanego ciała implikuje dodatkowe problemy. Dla przykładu, rozważymy statek kosmiczny lecący z Ziemi do Marsa. Już na początku statek będzie miał pewną prędkość związaną z ruchem wokół Ziemi – prędkość ta nie będzie brana pod uwagę, gdy statek będzie wchodził na orbitę transferową (okołosłoneczną). Aby okrążać Marsa, statek będzie również wymagał pewnej prędkości, ale na pewno mniejszej, niż potrzebna do dalszego orbitowania wokół Słońca. Najkorzystniej będzie zmniejszyć prędkość statku i pozwolić polu grawitacyjnemu Marsa na „pochwycenie” statku. Dzięki temu ilość energii potrzebnej przy obu impulsach będzie zminimalizowana. Przy takim locie decydujące znaczenie będzie miało wzajemne położenie obu planet – statek i planeta docelowa muszą spotkać się w tym samym punkcie ich własnych orbit (okołosłonecznych) w tym samym czasie. Dlatego też przy lotach międzyplanetarnych tak ważne jest tzw. okno startowe.

Manewr transferowy Hohmanna pozwala statkom kosmicznym przejść z niskiej orbity okołoziemskiej (LEO) na orbitę geostacjonarną w około 5 godzin (mówimy wtedy, że statek podróżuje po geostacjonarnej orbicie transferowej); z LEO do Księżyca w około 5 dni; z Ziemi do Marsa w około 260 dni.

Przemieszczanie się na dalsze odległości z użyciem manewru Hohmanna jest bardzo czasochłonne, dlatego loty do dalszych planet odbywają się zwykle przy udziale asysty grawitacyjnej, używanej czasem wielokrotnie, i tzw. międzyplanetarnej sieci transportowej.

Bibliografia

• Mechanika orbitalna (ang.)
• Classical Dynamics of Particles and Systems; S. Thornton, J. Marion; Brooks Cole, 2003, ISBN 0-534-40896-6.
• FernandF. Verger FernandF., The Cambridge encyclopedia of space, IsabelleI. Sourbès-Verger i inni, Cambridge, UK: Cambridge University Press, 2003, ISBN 0-521-77300-8, OCLC 49650047 .brak strony (książka)