Metaball

1. Wpływ dwóch „dodatnich” obiektów metaball na siebie (sumowanie).
2. Wpływ „ujemnej” kuli na „dodatnią” przez tworzenie wgłębienia w „dodatniej” kuli (odejmowanie).

Metaball – w grafice komputerowej obiekty przypominające wyglądem twory organiczne. Technika renderowania obiektów metaball została wynaleziona przez Jima Blinna we wczesnych latach osiemdziesiątych. W ogólności definiuje się jako obiekty dowolnego wymiaru, a więc jako funkcje w dziedzinie odpowiedniej liczby wymiarów, choć najczęściej stosuje się trój- i dwuwymiarowe implementacje (popularne w demach w latach 90). Elementem definicji jest wartość progowa (wielowymiarowej) objętości obiektu; w przypadku trójwymiarowym, gdzie $\scriptstyle i$-ty metaball opisany jest funkcją postaci $\scriptstyle \mathrm{metaball}_i(x, y, z)$ ma ona postać

$\sum_{i=0}^n \mathrm{metaball}_i(x,y,z) \leqslant \mbox{próg}$

i mówi, czy objętość zamknięta przez powierzchnię zdefiniowaną przez $\scriptstyle n$ obiektów metaball jest wypełniana w $\scriptstyle (x,y,z)$ czy nie.

Metaball są jednym ze sposobów tworzenia obiektów trójwymiarowych; modelowanie obiektów za ich pomocą (oraz obiektów metaedge) możliwe jest np. w programie LightWave 3D.

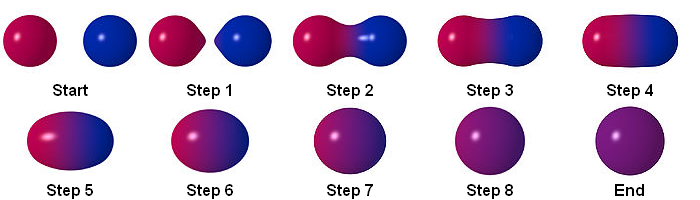
Interakcja dodatnia między dwoma dwuwymiarowymi obiektami metaball o różnych kolorach, stworzona w programie Bryce: dwa małe obiekty metaball łączą się w jeden większy.

Zobacz też

• metaedge
• marching cubes