Spektroskopia EPR
Spektroskopia EPR (spektroskopia elektronowego rezonansu paramagnetycznego, zwana również elektronowym rezonansem spinowym, ESR, dla odróżnienia od rezonansu cyklotronowego) – technika spektroskopii pozwalająca na wykrycie i uzyskanie informacji o otoczeniu danej próbki spinowej (tj. niesparowanych elektronów) w substancjach takich jak wolne rodniki, jony metali przejściowych, pierwiastki ziem rzadkich, aktynowce, defekty w dielektrykach i węglu oraz elektrony przewodnictwa w metalach i półprzewodnikach.
Podstawowe fizyczne założenia techniki są analogiczne do tych wykorzystywanych w spektroskopii NMR, ale badane są spiny elektronów, a nie spiny jąder atomowych. Z powodu różnic w masie pomiędzy jądrami a elektronami, w technice EPR używane są słabsze pola magnetyczne i wyższe częstotliwości promieniowania mikrofalowego niż w spektroskopii NMR. Dla elektronów, rezonans paramagnetyczny w polu magnetycznym o wartości ok. 0,3 T zachodzi przy częstotliwości ok. 10 GHz (tzw. pasmo X).
Spektroskopia EPR jest wykorzystywana m.in. w fizyce ciała stałego, w chemii do badań przebiegu reakcji oraz w biologii i medycynie do badania wolnych rodników poprzez śledzenie znaczników spinowych. Metoda EPR jest też stosowana do datowania w badaniach archeologicznych, np. wieku szkliwa zębów (hydroksyapatyt pochodzenia biologicznego).
Ponieważ wolne rodniki są bardzo reaktywne i krótko żyjące, nie występują one w układach biologicznych w wysokich stężeniach. Aby badać układy biologiczne zaprojektowano małoreaktywne molekuły (tzw. pułapki spinowe) mogące wiązać się w specyficznych miejscach w komórce czy białku.
Wstęp historyczny[edytuj | edytuj kod]
Badania rezonansu magnetycznego rozpoczyna praca Isaaka I. Rabiego z 1937 roku – Space Quantization in a Gyrating Magnetic Field[1]. Natomiast pierwsza obserwacja magnetycznego rezonansu została zaobserwowana w 1938 roku, w związku z techniką wiązek molekularnych[2]. Przez analogię poszukiwano podobnego zjawiska w układzie spinów jądrowych. Próbował to osiągnąć Cornelius Gorter, ale udało się dopiero Jewgienijowi Zawojskiemu w 1944 roku[3]. Zawojski w swoich badaniach w Kazaniu po raz pierwszy zaobserwował absorpcję rezonansową w solach metali przejściowych. Wyniki doświadczeń Zawojskiego objaśnił Jakow Frenkel jako elektronowy rezonans paramagnetyczny (1945). Już w pierwszych swoich pracach Zawojski stwierdził, że rezonansowa częstotliwość zmian pola jest proporcjonalna do częstotliwości pola mikrofalowego. Dla CrCl3 przy dwóch różnych częstotliwościach mikrofalowych: pierwszej = 2190 MHz i drugiej = 2760 MHz, uzyskano rezonans odpowiednio w polach o natężeniu 0,08 T i 0,1 T. Stąd uzyskano bardzo ważny związek między częstotliwością pola wysokich częstotliwości i natężeniem rezonansowego pola magnetycznego:
Stała uzyskana w doświadczeniu Zawojskiego wyniosła 27,5 GHz/T, co jest wartością zbliżoną do wartości 28 GHz/T, charakteryzującej elektron swobodny.
Teoria[edytuj | edytuj kod]

Jednostki i stałe[edytuj | edytuj kod]
Pole magnetyczne jest opisywane przez następujące jednostki i stałe:
- indukcja magnetyczna w teslach [T],
- natężenie pola magnetycznego w [A/m],
- związek i
- Jednostką CGS indukcji magnetycznej jest gaus [Gs] będący równowartością 10−4 [T].
Ponadto znajomość następujących stałych jest bardzo istotna:
- stała Plancka = 6,63·10−34 [J·s],
- stała Boltzmanna = 1,38·10−23 [J/K],
- magneton Bohra = 9,27·10−24 [J/T].
Podstawy[edytuj | edytuj kod]
Podstawę EPR stanowi efekt Zeemana polegający na rozszczepieniu poziomów energetycznych w paramagnetykach znajdujących się w polu magnetycznym. Po umieszczeniu próbki o momencie magnetycznym w polu magnetycznym osiąga ona energię
Dla atomu o całkowitym momencie pędu całkowity dipolowy moment magnetyczny
gdzie:
- – współczynnik rozszczepienia spektroskopowego.
Energia atomu po umieszczeniu w polu magnetycznym:
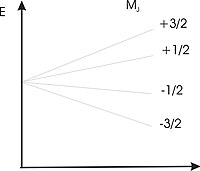
Wektor każdego atomu może posiadać jedynie niektóre dozwolone orientacje determinowane przez zbiór wartości liczby kwantowej Jest to przyczyną ograniczenia energii do zbioru
gdzie:
W zewnętrznym polu magnetycznym rozszczepienie pojedynczego poziomu na podpoziomów zwane jest rozszczepieniem zeemanowskim. Jeżeli na stałe pole magnetyczne nałożymy zmienne pole magnetyczne o odpowiedniej częstotliwości w próbce zaczną zachodzić przejścia pomiędzy poziomami zeemanowskimi. Przejścia te zależne są od:
- możliwe tylko przejścia pomiędzy sąsiednimi poziomami
- warunek dopasowania energetycznego
Rozkład Boltzmanna[edytuj | edytuj kod]
W praktyce nigdy nie mamy do czynienia z pojedynczą próbką, ale z populacją próbek z wieloma centrami paramagnetycznymi. Jeżeli ta konfiguracja znajdzie się w stanie równowagi termicznej, obsadzenie poziomów energetycznych jest opisywane przez rozkład Boltzmanna
gdzie:
- – liczba cząstek obsadzających poziom
- – stała Boltzmanna,
- – temperatura w stopniach kelwinach.
Dla pasma X ( = 10 GHz) i pokojowej temperatury stosunek jest równy 0,998, ponieważ niższy poziom zawiera więcej elektronów niż wyższy i przejścia z „dołu na górę” są bardziej prawdopodobne.
Podstawowe równanie EPR to:
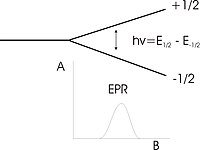
Obserwację sygnału EPR można prowadzić mierząc zmiany rezonansowej absorpcji energii w zależności od częstotliwości promieniowania elektromagnetycznego przy stałej wartości indukcji pola magnetycznego. Z drugiej strony możemy prowadzić pomiary odwrotnie, zmieniając pole magnetyczne przy stałej częstotliwości Z powodów technicznych drugi sposób jest wygodniejszy.
W przypadku czysto spinowego magnetyzmu ( = 2,0) i częstotliwości absorpcja energii następuje w polu magnetycznym o indukcji:
Dla najczęściej używanej częstotliwości = 9,5 GHz (pasmo X mikrofal), rezonans zachodzi przy = 0,34 T (3400 Gs).
Parametry widma EPR[edytuj | edytuj kod]
Współczynnik rozszczepienia spektralnego [edytuj | edytuj kod]
Znajomość współczynnika (współczynnik magnetogiryczny, gyromagnetyczny) daje informacje o strukturze centrum paramagnetycznego. Dla wolnych rodników i jonów w fazie stałej bądź ciekłej spin elektronu jest silnie powiązany ze środowiskiem i nie może występować w dowolnym ułożeniu w polu magnetycznym. Prowadzi to do zjawiska zamrażania orbitalnego momentu magnetycznego w sieci krystalicznej. Z tego powodu parametr sygnału EPR dla wielu paramagnetycznych atomów w skondensowanych fazach wynosi = 2,002256, gdzie dodatek 0,002256 pochodzi od relatywistycznej poprawki związanej z ruchem elektronów w atomie. W przypadku wolnego jonu, współczynnik posiada właściwości izotropowe. W krysztale natomiast wartość zależy od kierunku zewnętrznego pola magnetycznego.
Definicja szerokości linii rezonansowej[edytuj | edytuj kod]
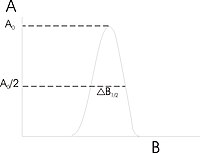
Szerokości linii rezonansowej wyraża się w jednostkach indukcji magnetycznej i mierzone są wzdłuż osi odciętych od środka linii do linii rzędnej przechodzącej przez wybrany punkt krzywej. Tak zdefiniowane szerokości mają tę zaletę, że dla linii asymetrycznej można podawać szerokości połówkowe. Szerokość połówkowa jest to dystans od centrum linii do punktu w którym absorpcja wynosi połowę maksymalnej wartości w środku linii rezonansowej. Pierwsza szerokość nachyleniowa jest to odległość od środka linii do punktu o maksymalnym nachylenia krzywej absorpcji.
Amplituda linii rezonansowej[edytuj | edytuj kod]
Amplituda stanowi orientacyjną miarę stężenia niesparowanych elektronów w badanym materiale. Umożliwia także, często w sposób selektywny, śledzenie kinetyki zjawisk skojarzonych ze zmianą liczby niesparowanych elektronów. Ubytek ilości niesparowanych elektronów powoduje spadek amplitudy sygnału i intensywności absorpcji EPR[4][5].
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ I.I. Rabi, J.R. Zacharias, S. Millman, P. Kuch, Phys. Rev. 53, 318 (1938); Phys. Rev. 55, 526 (1939).
- ↑ F.N. Ramsey, Molecular Beams, Clarendon Press 1956.
- ↑ E. Zawojski, Paramagnetic Absorption in Perpendicular and Parallel Fields for Salts, Solutions and Metals, 1944.
- ↑ S.J. Łukiewicz: Spektroskopia in vivo elektronowego rezonansu paramagnetycznego w biologii i medycynie. W: Praca zbiorowa pod red. L. Filipczyńskiego i W. Torbicza: Problemy Biocybernetyki i Inżynierii Biomedycznej. Tom 2: Biopomiary. Warszawa: WKiŁ, 1990, s. 329–366.
- ↑ Z. Kęcki: Podstawy spektroskopii molekularnej. Warszawa: PWN, 1992.
Linki zewnętrzne[edytuj | edytuj kod]
- Lista laboratoriów spektroskopii EPR w Polsce



































