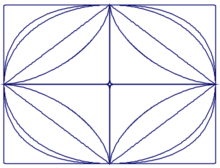
Superelipsa
Superelipsa, krzywa Lamé – krzywa płaska opisana we współrzędnych kartezjańskich równaniem:
gdzie oraz i są „promieniami” superelipsy. W przypadku otrzymuje się elipsę, w przypadku – romb o przekątnych oraz Gdy zwiększana jest do nieskończoności, krzywa zaczyna coraz bardziej przypominać prostokąt, natomiast gdy dąży do zera, krzywa dąży do „krzyża”.
Superelipsa może być też opisana parą równań parametrycznych:
gdzie:
Krzywe te zostały opisane przez francuskiego matematyka Gabriela Lamé. Spopularyzował je Duńczyk Piet Hein w architekturze i przy projektowaniu przedmiotów codziennego użytku.
Uogólnienia[edytuj | edytuj kod]
Superelipsa jest szczególnym przypadkiem superformuły. Odpowiednikiem superelipsy w przestrzeni trójwymiarowej jest Superquadrics.
Zobacz też[edytuj | edytuj kod]
Linki zewnętrzne[edytuj | edytuj kod]
- Eric W. Weisstein, Superellipse, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12] (ang.).