Liczba Hittorfa
Liczba Hittorfa, liczba przenoszenia jonów ( i ) – stosunek wielkości ładunku elektrycznego, przenoszonego w czasie elektrolizy przez jony jednego rodzaju, do całkowitego ładunku, przenoszonego przez wszystkie jony danego elektrolitu.
Odkrycie zjawiska[edytuj | edytuj kod]
Pojęcie „liczby przenoszenia jonów”, znanej współcześnie jako „liczba Hittorfa”, wprowadził Johann Wilhelm Hittorf, kontynuator przełomowych badań Faradaya i Daniella z lat 30. XIX wieku, dotyczących przewodnictwa elektrolitów. Swoje najważniejsze badania, dotyczące zmian stężenia w czasie elektrolizy, Hittorf wykonał w latach 1853–1859. Stosując elektrolizer własnej konstrukcji, wykazał, że zmiany stężenia w obu przestrzeniach przyelektrodowych nie są jednakowe, co można wyjaśnić, przypisując różnym jonom niejednakowe zdolności do transportowania ładunku elektrycznego przez dany roztwór (różne ruchliwości, od których zależą udziały w przenoszeniu ładunków, nazwane „liczbami przenoszenia”). Propozycje Hittorfa nie od razu zyskały aprobatę, jednak już w latach 70. i 80. XIX w. zostały z powodzeniem wykorzystane przez Kohlrauscha i Arrheniusa – twórców podstaw dzisiejszej wiedzy nt. przewodnictwa roztworów i dysocjacji elektrolitów[1][2].
Informacje podstawowe[edytuj | edytuj kod]

• K, A, S – przestrzenie przyelektrodowe elektrolizera (katodowa i anodowa) i przestrzeń wewnętrzna (roztwór elektrolitu o stałym stężeniu),
• kółka – symbole kationów (czerwone) i anionów (zielone), uporządkowane w szeregi w celach poglądowych,
• góra – stan roztworu przed elektrolizą,
• środek – stan po przeniesieniu przez granice między strefami pięciu kationów i jednego anionu,
• dół – stan roztworu po elektrochemicznej redukcji 6 kationów i utlenieniu 6 anionów.
Udziały obu rodzajów jonów w przenoszeniu ładunków wynoszą 5/6 dla kationów i 1/6 dla anionów, co jest konsekwencją założenia o pięciokrotnie większej ruchliwości kationów. Udziały – liczby przenoszenia jonów – mogą być wyznaczane doświadczalnie, poprzez określanie zmian stężenia w przestrzeniach przyelektrodowych (ubytek stężenia przy katodzie jest 5 razy większy od ubytku przy anodzie).
Przewodnictwo elektrolitów polega na przemieszczaniu się jonów obydwu znaków pod wpływem pola elektrycznego. Różne rodzaje jonów poruszają się w różnych kierunkach (kationy w stronę katody, aniony w stronę anody) i z różną szybkością (mają różną ruchliwość). Szybkość ruchu jonów w polu o określonym gradiencie potencjału (zob. potencjał elektryczny a natężenie pola elektrycznego) zależy od sił wzajemnego oddziaływania elektrostatycznego jonów, ich mas i średnic oraz stopnia solwatacji, temperatury, lepkości cieczy. Jony jednego rodzaju zawarte w jednostce objętości elektrolitu, przenoszą ładunek [3][4][5][6]:
a wszystkie jony:
gdzie[6]:
- – stężenie jonów określające ich liczbę w jednostce objętości,
- – ładunek jonów,
- – ruchliwość jonów (prędkość w polu o jednostkowym gradiencie potencjału).
Liczba Hittorfa, określana dla jonów jest stosunkiem wielkości przenoszonego przez nie ładunku elektrycznego do ładunku przenoszonego przez wszystkie jony [6][7][8]:
co można wyrazić również, korzystając z pojęcia równoważnikowych przewodnictw jonowych i równoważnikowego przewodnictwa elektrolitu [7][8]
- i
Wyznaczanie liczb przenoszenia jonów[edytuj | edytuj kod]
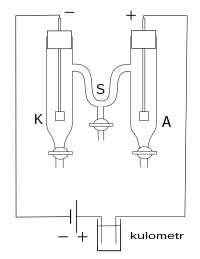
Zaproponowana przez Johanna Hittorfa metoda pomiarów polega na oznaczaniu zmian stężenia elektrolitu w pobliżu elektrod. Stosowany jest aparat zaprojektowany przez Hittorfa, umożliwiający pobranie próbek cieczy z każdej przestrzeni – katodowej (K), anodowej (A) i wewnętrznej (S), bez ich mieszania[9]. Na rurkach łączących przestrzenie K, S i A bywają umieszczane zawory, zamykające połączenie po przeniesieniu ładunku Q, którego wielkość jest oznaczana z użyciem kulometru[10][11].
Materiał, z którego są wykonywane elektrody, zależy od składu badanych roztworów, np. w przypadku badań roztworów azotanu srebra anodą jest metaliczne srebro (utleniające się do Ag+), natomiast katoda (miejsce redukcji anionów) może być wykonana ze srebra, platyny lub innego metalu szlachetnego[12].
Metoda Hittorfa jest nadal stosowana, jeżeli badane roztwory są rozcieńczone. W tych przypadkach błędy spowodowane takimi czynnikami, jak wzajemne oddziaływania międzycząsteczkowe (w tym oddziaływania jon-jon), dyfuzja, konwekcja lub mechaniczne mieszanie, są przyczyną niewielkich błędów. W czasie obliczeń (sporządzanie bilansów ładunków) stężenia bywają wyrażane w gramorównoważnikach w jednostce objętości[a][6][12].
Procedura dokładniejszych oznaczeń liczb Hittorfa nosi nazwę metody poruszającej się granicy (Mc Innes i współpracownicy, 1925[1][10]).
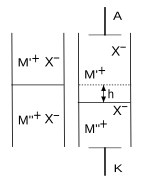
W wersji z jedną powierzchnią graniczną pionowo umieszczoną rurkę wypełnia się dwoma roztworami o różnej gęstości oraz różnym współczynniku załamania światła. Na roztwór o większej gęstości nalewa się drugi roztwór w taki sposób, aby granica między cieczami była wyraźna („nawarstwianie”). Granica między roztworami jest wyraźnie widoczna dzięki różnym współczynnikom załamania. Jedna z cieczy (często warstwa górna) jest roztworem badanej soli (na poglądowym rysunku symbol M′X), druga – „wskaźnikowym” roztworem soli o wspólnym jonie z solą badaną („sól wskaźnikowa” M′′X)[10][13][14]. W polu elektrycznym zachodzi wędrówka kationów i anionów do odpowiednich elektrod, co jest przyczyną przesuwania się granicy między roztworami M′X i M′′X. Jej rozmywaniu się zapobiega takie dobranie stężeń elektrolitów, aby ruchliwości obu kationów były jednakowe lub zbliżone, co oznacza spełnienie zależności („funkcja regulująca Kohlrauscha”)[15][16]:
Poszukiwana wartość liczby Hittorfa dla kationu M′+ jest obliczana z zależności:
gdzie:
- – wielkość przeniesionego ładunku,
- – wielkość ładunku przeniesionego przez kationy,
- – stała Faradaya, (ładunek elektryczny przypadający na jeden mol elektronów),
- – stężenie, [[[gramorównoważnik|wal]]/dm³],
- – objętość roztworu między początkowym i końcowym położeniem przesuwającej się granicy, [cm³].
W przypadku kolejnego nawarstwienia na roztwór dolny dwóch wyższych warstw, określanie wielkości przesunięcia dwóch granic umożliwia równoczesne wyznaczenie dwóch liczb Hittorfa. Nawarstwienie na roztwór CH3COONa roztworu NaCl (wspólny kation), a następnie roztworu LiCl (wspólny anion) pozwala określić wartości liczby przenoszenia jonów chlorkowych i sodowych, korzystając z równań[17]:
- i
w których ruchliwości i są zastępowane odpowiednimi wielkościami przesunięcia granic 1→1′ i 2→2′. Metoda nie jest stosowana często, ponieważ równoczesne spełnienie wymagań „funkcji regulującej Kohlrauscha” na dwóch granicach między roztworami jest kłopotliwe (odrębne oznaczenie liczby charakterystycznej dla każdego z jonów jest łatwiejsze)[17].
Przykładowe wartości liczb przenoszenia[edytuj | edytuj kod]
Liczby przenoszenia kilku kationów w 0,1 n roztworach ich chlorków wynoszą[10]:
Zależność t od stężenia elektrolitów[edytuj | edytuj kod]
Mimo zmniejszania się ruchliwości jonów wraz ze wzrostem stężenia elektrolitu, liczby przenoszenia jonów zachowują zwykle niemal stałą wartość, dopóki utrzymuje się stan całkowitej dysocjacji. Jest to wyjaśniane zmniejszaniem się prędkości anionów i kationów w podobnym stopniu. Gdy stężenie zmierza do zera, wartości i dążą do wartości granicznych i które mogą być wyznaczane metodą ekstrapolacji[18].
W przypadkach szczególnych bywa obserwowana silna zależność wartości i od stężenia (niekiedy w wyniku pomiarów uzyskuje się nawet pozbawione sensu wartości t=0 lub t<0). Jest to najczęściej związane z powstawaniem w stężonych roztworach kompleksów anionów z kationami. Ilustruje to przykład roztworów NiCl2, w których obok jonów Ni2+ i Cl- powstają jony NiCl+ (część chloru zaczyna wędrować w kierunku katody). W stężonych roztworach CdJ2 dysocjacja może prowadzić do powstawania jonów kompleksowych CdJ2−4, przenoszących kadm w kierunku anody[18].
Uwagi[edytuj | edytuj kod]
- ↑ Związek między gramorównoważnikiem i molem określa się, biorąc pod uwagę ładunek powstających jonów, co ilustrują przykłady: AgNO3: 1 gramorównoważnik = 1 mol; MgCl2: 1 gramorównoważnik = ½ mola; CuSO4: 1 gramorównoważnik = ½ mola (po całkowitej dysocjacji 1 mola ładunek kationów/anionów jest równy stałej Faradaya, ). Ilość kationów i anionów, wyrażona w gramorównoważnikach, jest wyrażana jako iloczyn i
Przypisy[edytuj | edytuj kod]
- ↑ a b Michael Spiro: Historical Highlights in Transference Number Research. W: Electrochemistry, Past and Present. John T. Stock, Mary Virginia Orna (red.). American Chemical Society, 1989, s. 92–114, seria: ACS Symposium Series, Vol. 390. DOI: 10.1021/bk-1989-0390.ch007.
- ↑ Hittorf, Johann Wilhelm. [w:] Complete Dictionary of Scientific Biography [on-line]. www.encyclopedia.com. s. 2008. [dostęp 2014-12-11]. (ang.).
- ↑ Basiński, Bielański i Gumiński 1966 ↓, s. 684–691.
- ↑ Bursa 1979 ↓, s. 684–688.
- ↑ Miłek, Obrębska i Podkowińska-Kalita 1989 ↓, s. 147–150.
- ↑ a b c d Jarosław Dąbek: Ćwiczenie 2. Liczby przenoszenia. [w:] Laboratorium z chemii fizycznej [on-line]. agh.edu.pl. [dostęp 2018-08-09]. [zarchiwizowane z tego adresu (2016-03-04)].
- ↑ a b Basiński, Bielański i Gumiński 1966 ↓, s. 686.
- ↑ a b Bursa 1979 ↓, s. 684.
- ↑ Miłek, Obrębska i Podkowińska-Kalita 1989 ↓, s. 307–308.
- ↑ a b c d Basiński, Bielański i Gumiński 1966 ↓, s. 689.
- ↑ a b Miłek, Obrębska i Podkowińska-Kalita 1989 ↓, s. 307.
- ↑ a b Basiński, Bielański i Gumiński 1966 ↓, s. 687.
- ↑ Bursa 1979 ↓, s. 687–688.
- ↑ a b Miłek, Obrębska i Podkowińska-Kalita 1989 ↓, s. 309.
- ↑ a b Basiński, Bielański i Gumiński 1966 ↓, s. 690.
- ↑ Bursa 1979 ↓, s. 687.
- ↑ a b Miłek, Obrębska i Podkowińska-Kalita 1989 ↓, s. 310.
- ↑ a b Basiński, Bielański i Gumiński 1966 ↓, s. 691.
Bibliografia[edytuj | edytuj kod]
- Antoni Basiński, Adam Bielański, Kazimierz Gumiński, Chemia fizyczna, wyd. 3, Warszawa: Państwowe Wydawnictwo Naukowe, 1966, s. 676–694.
- Stanisław Bursa: Chemia fizyczna. Wyd. 2 popr. Warszawa: Państwowe Wydawnictwo Naukowe, 1979, s. 678−692. ISBN 83-01-00152-6.
- Ryszard Miłek, Maria Obrębska, Maria Podkowińska-Kalita: Chemia fizyczna. Ćwiczenia laboratoryjne z elementami teorii. Wyd. 2. Warszawa: Wydawnictwa Politechniki Warszawskiej, 1989, s. 147–150, 307–311. (s. 307–311 pdf)
Linki zewnętrzne[edytuj | edytuj kod]
- transport number, t, [w:] A.D. McNaught, A. Wilkinson, Compendium of Chemical Terminology (Gold Book), S.J. Chalk (akt.), International Union of Pure and Applied Chemistry, wyd. 2, Oxford: Blackwell Scientific Publications, 1997, DOI: 10.1351/goldbook.T06489, ISBN 0-9678550-9-8 (ang.).
- Hittorfa liczba, [w:] Encyklopedia PWN [dostęp 2014-12-19].
- Hittorfa liczba. encyklopedia.interia.pl. [dostęp 2014-12-19].
- Hittorfa liczba. [w:] Encyklopedia WIEM [on-line]. [dostęp 2014-12-19]. [zarchiwizowane z tego adresu (2014-12-14)].
- Wyznaczanie liczb przenoszenia. www.pg.gda.pl. [dostęp 2014-12-19].
- Andrzej Molski: Wyznaczanie liczb przenoszenia jonów K+ i OH−. [dostęp 2014-12-19]. [zarchiwizowane z tego adresu (2014-12-14)].
- Instrukcje do ćwiczeń laboratoryjnych dla kierunku Lekarskiego. Ćw. M1 Wyznaczenie liczby przenoszenia oraz ruchliwości jonów w przewodnikach jonowych. Uniwersytet Warmińsko-Mazurski, Wydział Nauki o Żywności, Katedra Fizyki i Biofizyki. [dostęp 2014-12-19].