Ekstremum funkcji

Ekstrema lokalne funkcji $f(x)=2x^{3}-9x^{2}+12x-3$ zaznaczone kolorem niebieskim (właściwe maksimum lokalne) i czerwonym (właściwe minimum lokalne)

Ekstremum funkcji (l. mn. ekstrema; z łac. extrēmus – najdalszy, ostatni) – maksymalna lub minimalna wartość funkcji.

• Funkcja $f(x)$ przyjmuje w punkcie $x_{0}$ maksimum lokalne (odpowiednio: minimum lokalne), jeśli w pewnym otwartym otoczeniu tego punktu (np. w pewnym przedziale otwartym) funkcja nigdzie nie ma wartości większych (odpowiednio: mniejszych).
• Jeśli dodatkowo w pewnym otwartym sąsiedztwie punktu $x_{0}$ funkcja nie ma również wartości równych $f(x_{0}),$ to jest to maksimum (odpowiednio: minimum) lokalne właściwe.
• Minima i maksima lokalne są zbiorczo nazywane ekstremami lokalnymi.
• Największa i najmniejsza wartość funkcji w całej dziedzinie nazywane są odpowiednio maksimum i minimum globalnym, a zbiorczo ekstremami globalnymi.

Obrazowo: Na powierzchni Ziemi maksimum globalne wysokości nad poziomem morza występuje na szczycie Mount Everestu, maksimum lokalnym jest szczyt każdego pagórka. Jeśli szczyt pagórka jest poziomy i płaski (a także niekiedy w innych przypadkach), nie będzie to maksimum lokalne właściwe.

Istnieją funkcje nieposiadające ekstremów lokalnych ani globalnych, np. funkcja $f(x)=x.$

Poszukiwanie ekstremów jest ważne w praktycznych zastosowaniach matematyki, na przykład w technice i statystyce. Wiele zagadnień optymalizacyjnych sprowadza się do poszukiwania ekstremów odpowiednich funkcji, jak na przykład funkcji kosztu, albo miary jakości dla różnych parametrów danego urządzenia.

Teoria ekstremów w naturalny sposób ma silny związek z teorią nierówności: wiele problemów i twierdzeń można formułować równoważnie zarówno w języku ekstremów, jak i nierówności, co rzuca światło na obie te dziedziny.

Funkcje, dla których można rozważać ekstrema

Funkcja jako przyporządkowanie

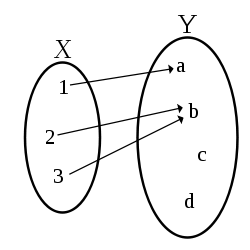
W matematyce wartością funkcji nie musi być koniecznie liczba – funkcją jest dowolne przyporządkowanie każdemu elementowi zbioru zwanego dziedziną po jednym elemencie zbioru zwanego przeciwdziedziną. Funkcją jest więc również przyporządkowanie każdemu łysemu aktorowi Teatru Wielkiego koloru włosów jego ulubionej peruki.

Pojęcie ekstremum wymaga, by wartości funkcji dało się ze sobą porównywać – w przeciwdziedzinie funkcji powinien być zatem zdefiniowany jakiś porządek. Zbiór uporządkowany, i to liniowo, tworzą np. liczby rzeczywiste. Nie ma natomiast powszechnie przyjętego uporządkowania kolorów, zwłaszcza porządku liniowego.

W przypadku ekstremum lokalnego konieczne jest ponadto sprecyzowanie pojęcia „lokalności”. Dokonuje się to przez określenie dla każdego argumentu funkcji, które punkty z jej dziedziny są mu „bliskie”. Formalizując to podejście, określamy w każdym punkcie dziedziny funkcji tak zwaną bazę otoczeń punktu. Dla liczby rzeczywistej otoczeniem jest np. przedział otwarty, zawierający tę liczbę. Ogólnie, zbiór z systemem otoczeń, spełniającym pewne naturalne warunki tworzy tzw. przestrzeń topologiczną.

O ekstremach lokalnych można zatem mówić w przypadku dowolnej funkcji, której dziedzina jest przestrzenią topologiczną, a przeciwdziedzina zbiorem częściowo uporządkowanym. Ze względu na zastosowania najczęściej rozważa się szczególny przypadek – funkcje rzeczywiste, czyli funkcje o wartościach w liczbach rzeczywistych, których dziedzina jest podzbiorem skończenie wymiarowej przestrzeni euklidesowej.

Definicje

Funkcja $f$ o wartościach w zbiorze uporządkowanym określona na przestrzeni topologicznej ma w punkcie $x_{0}$ tej przestrzeni:

• minimum lokalne, jeśli istnieje otoczenie otwarte $U$ punktu $x_{0}$ takie, że dla każdego $x\in U,$

$f(x)\geqslant f(x_{0}),$

więc nie występują w okolicy punktu $x_{0}$ wartości funkcji mniejsze od $f(x_{0})$ (ani nieporównywalne), choć mogą występować wartości równe,

• maksimum lokalne, gdy istnieje otoczenie otwarte $U$ punktu $x_{0}$ takie, że dla każdego $x\in U,$

$f(x)\leqslant f(x_{0}),$

więc nie występują w okolicy punktu $x_{0}$ wartości funkcji większe od $f(x_{0})$ (ani nieporównywalne), choć mogą występować wartości równe,

• właściwe minimum lokalne, jeśli w pewnym otoczeniu otwartym $U$ punktu $x_{0}$ funkcja przyjmuje wszędzie, z wyjątkiem tego punktu, wartości większe od $f(x_{0}),$ czyli nie ma wartości równych dla $x\neq x_{0},$ formalnie:

$x=x_{0}\vee f(x)>f(x_{0})$ dla każdego $x\in U,$

• właściwe maksimum lokalne, jeśli w pewnym otoczeniu otwartym $U$ punktu $x_{0}$ funkcja przyjmuje wszędzie, z wyjątkiem tego punktu, wartości mniejsze od $f(x_{0}),$ formalnie:

$x=x_{0}\vee f(x)<f(x_{0})$ dla każdego $x\in U.$

Funkcja $f$ o wartościach w zbiorze uporządkowanym ma w punkcie $x_{0}$ swojej dziedziny:

• minimum globalne, jeśli dla każdego $x$ należącego do jej dziedziny:

$f(x)\geqslant f(x_{0}),$

• maksimum globalne, jeśli dla każdego $x$ należącego do jej dziedziny:

$f(x)\leqslant f(x_{0}),$

• właściwe minimum globalne, jeśli dla każdego $x$ należącego do jej dziedziny:

$x=x_{0}\vee f(x)>f(x_{0}),$

czyli funkcja przyjmuje wszędzie z wyjątkiem punktu $x_{0}$ wartości większe od $f(x_{0})$

• właściwe maksimum globalne, jeśli dla każdego $x$ należącego do jej dziedziny:

$x=x_{0}\vee f(x)<f(x_{0}),$

czyli funkcja przyjmuje wszędzie z wyjątkiem punktu $x_{0}$ wartości mniejsze od $f(x_{0}).$

Nie każda funkcja posiada ekstrema. Jeśli funkcja nie jest ograniczona (np. $f(x)=x$), to nie ma maksimum ani minimum globalnego – jeżeli nie jest ograniczona od góry, to nie ma maksimum globalnego; a jeżeli od dołu, to nie ma minimum globalnego.

Można też mówić o maksimach i minimach w podzbiorze dziedziny – są to wówczas największe lub najmniejsze wartości funkcji dla argumentów z tego podzbioru.

Funkcje rzeczywiste jednej zmiennej

Proste przykłady ekstremów

• 
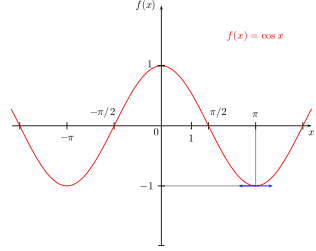
  Funkcja cosinus osiąga maksimum dla każdej parzystej wielokrotności $\pi ,$ czyli $\dots ,-4\pi ,-2\pi ,0,2\pi ,4\pi ,\dots$ oraz minimum dla każdej nieparzystej wielokrotności $\pi ,$ czyli $\dots ,-5\pi ,-3\pi ,-\pi ,\pi ,3\pi ,5\pi ,\dots$ Są to lokalne ekstrema właściwe i jednocześnie ekstrema globalne (ale nie globalne ekstrema właściwe!).
• 
  Funkcja kwadratowa $f(x)=x^{2}$ osiąga właściwe minimum (lokalne i globalne) dla $x=0.$ Nie ma maksimum, nawet lokalnego. Dla każdego argumentu można w jego bezpośrednim sąsiedztwie wskazać punkt w którym funkcja przyjmuje większą wartość.
• 
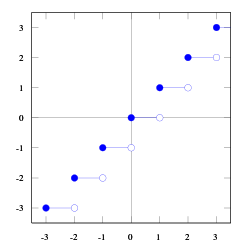
  Funkcja entier osiąga w każdym punkcie maksimum lokalne niewłaściwe. Minimum lokalne występuje jednak tylko dla liczb niecałkowitych. W każdym otoczeniu liczby całkowitej z lewej strony występują mniejsze wartości funkcji. Nie ma ekstremów globalnych.
• 
  Funkcja $f(x)=\left\{{\begin{array}{l}{x^{2}(1+\sin {\frac {1}{x}}),\;x\neq 0}\\{0,\;x=0}\end{array}}\right.$ ma w punkcie $x_{0}=0$ minimum lokalne, jednak nie jest to minimum właściwe – w dowolnej bliskości tego punktu można znaleźć inne punkty, w których przyjmuje ona tę samą wartość (oprócz tego posiada nieskończoną liczbę minimów i maksimów właściwych).

Przykład – właściwe minimum lokalne w każdym punkcie dziedziny

Fragment wykresu funkcji $f\colon \mathbb {Q} \ni {\frac {p}{q}}\mapsto \left|{\frac {q}{\operatorname {NWD} (p,q)}}\right|,$ mającej właściwe minimum w każdym punkcie swojej dziedziny. Kropki – punkty $\left({\frac {p}{q}},q\right)$ odpowiadają nieskracalnym ułamkom ${\frac {p}{q}}$

Niech funkcja $f$ przyporządkowuje każdej liczbie wymiernej wartość mianownika wyrażającego ją ułamka skróconego. Formalnie:

$f\colon \mathbb {Q} \ni {\frac {p}{q}}\mapsto \left|{\frac {q}{\operatorname {NWD} (p,q)}}\right|,$

gdzie NWD oznacza największy wspólny dzielnik.

Dla dowolnego wymiernego $x$ istnieje otoczenie otwarte, w którym wszystkie inne liczby wymierne mają większy mianownik, a więc większą wartość funkcji $f$. A zatem funkcja ta ma dla każdej liczby wymiernej (czyli dla każdego punktu swojej dziedziny) właściwe minimum lokalne.

Warunek wystarczający ekstremum globalnego (twierdzenie Weierstrassa)

Z twierdzenia Weierstrassa wiadomo, że funkcja ciągła o wartościach rzeczywistych, określona na zbiorze zwartym (a więc np. na przedziale domkniętym), osiąga ekstrema globalne. Twierdzenie to jest prawdziwe w pełnej ogólności – a więc nie tylko dla funkcji liczbowych, a dla dowolnych funkcji ciągłych, określonych na zwartych podzbiorach dowolnych przestrzeni topologicznych.

Funkcje różniczkowalne

W dalszej części sekcji rozważane będą funkcje $f\colon [a,b]\to \mathbb {R}$ ciągłe oraz różniczkowalne w przedziale $(a,b).$ Geometrycznie oznacza to, że ich wykres jest „nieprzerwany” i „gładki”, czyli ma w każdym punkcie styczną.

Warunek konieczny istnienia ekstremum lokalnego (twierdzenie Fermata)

Funkcja $g(x)=x^{3}$ nie ma dla $x=0$ ekstremum lokalnego, mimo że jej pochodna w tym punkcie jest równa zero

Warunkiem koniecznym istnienia ekstremów lokalnych różniczkowawalnych funkcji $f$ w pewnym punkcie $x_{0}\in (a,b)$ jest

$f'(x_{0})=0.$

Geometrycznie oznacza to, że styczna do wykresu funkcji jest w tym punkcie prostą poziomą. Jest to tzw. twierdzenie Fermata. Udowodnijmy je:

jeśli $f$ ma w punkcie $x_{0}$ ekstremum lokalne, to istnieje takie $\epsilon >0,$ że dla każdej liczby rzeczywistej $h,$ spełniającej $0<|h|<\epsilon ,$ zachodzi:

$(f(x_{0}-h)-f(x_{0}))\cdot (f(x_{0}+h)-f(x_{0}))\geqslant 0,$

a więc:

${\frac {f(x_{0}-h)-f(x_{0})}{-h}}\cdot {\frac {f(x_{0}+h)-f(x_{0})}{h}}\leqslant 0.$

Po przejściu do granicy, dla $h\to 0,$ otrzymujemy:

$(f'(x_{0}))^{2}\leqslant 0.$

Zatem $f'(x_{0})=0.$

Warunek Fermata nie jest jednak wystarczający. Np. funkcja $g(x)=x^{3}$ nie ma ekstremum, chociaż jej pochodna $g'(x)=3x^{2}$ zeruje się dla $x_{0}=0.$ Ekstremum może natomiast istnieć w punktach, w których nie istnieje (obustronna) pochodna skończona:

• funkcja $h(x)=x^{\frac {2}{3}}$ ma na przykład, minimum w punkcie $x_{0}=0,$ podczas gdy jej pochodna lewostronna w tym punkcie równa się $-\infty ,$ a prawostronna $+\infty ;$
• podobnie funkcja wartość bezwzględna ma w punkcie $x_{0}=0$ minimum globalne, chociaż w tym punkcie nie jest różniczkowalna.

Warunek konieczny i wystarczający istnienia ekstremum lokalnego

Funkcja ciągła $f\colon [a,b]\to \mathbb {R} ,$ różniczkowalna w przedziale $(a,b)$ i mająca skończoną liczbę punktów stacjonarnych (tj. takich, w których zeruje się jej pierwsza pochodna) ma w punkcie $x_{0}\in (a,b){:}$

• minimum lokalne wtedy i tylko wtedy, gdy istnieje takie $\delta >0,$ że:
  • $f'(x_{0})=0,$
  • $f'(x)<0$ dla $x\in (x_{0}-\delta ,x_{0}),$
  • $f'(x)>0$ dla $x\in (x_{0},x_{0}+\delta );$

• maksimum lokalne wtedy i tylko wtedy, gdy istnieje takie $\delta >0,$ że
  • $f'(x_{0})=0,$
  • $f'(x)>0$ dla $x\in (x_{0}-\delta ,x_{0}),$
  • $f'(x)<0$ dla $x\in (x_{0},x_{0}+\delta ).$

Inne warunki wystarczające istnienia ekstremów

Jeśli o funkcji $f,$ określonej jak wyżej, założy się dodatkowo, że jest dwukrotnie różniczkowalna w przedziale $(a,b)$ oraz jej druga pochodna jest ciągła, to jeżeli $f'(x_{0})=0$ i $f''(x_{0})\neq 0,$ to funkcja $f$ ma w punkcie $x_{0}$ ekstremum, przy czym, gdy $f''(x_{0})<0,$ to jest to maksimum lokalne, a gdy $f''(x_{0})>0,$ to minimum lokalne.

Powyższe kryterium nie rozstrzyga przypadku, gdy druga pochodna jest równa zero.

Kryterium istnienia ekstremów funkcji n-krotnie różniczkowalnych

Jeżeli założy się dodatkowo o funkcji $f,$ że jest $n$-krotnie razy różniczkowalna i $n$-ta pochodna jest ciągła w $(a,b),$ to zachodzi następujące twierdzenie:

jeżeli

$f'(x_{0})=f''(x_{0})=\ldots =f^{(n-1)}(x_{0})=0,$

tj. wszystkie pochodne do $(n-1)$-ej zerują się w punkcie $x_{0},$ a $n$-ta pochodna jest różna od zera, to

• gdy $n$ jest liczbą parzystą, to $f$ ma ekstremum w punkcie $x_{0},$ przy czym jest to maksimum, gdy $f^{(n)}(x_{0})<0$ lub minimum, gdy $f^{(n)}(x_{0})>0,$
• gdy $n$ jest liczbą nieparzystą, ekstremum nie istnieje.

Dowód

Z założenia zerowania się pochodnych do $(n-1),$ można wyprowadzić korzystając ze wzoru Taylora:

$f(x_{0}+h)-f(x_{0})={\frac {h^{n}}{n!}}f^{(n)}(x_{0}+\theta h)$

dla pewnego $0<\theta <1.$

Jeśli $n$ jest parzyste, rozumowanie przebiega jak poprzednio. Gdy $n$ jest nieparzyste, prawa strona równości zmienia znak, gdy $h$ zmienia znak, a funkcja $f^{(n)}$ zachowuje w pewnym otoczeniu punktu $x_{0}$ ten sam znak co $x_{0}.$ Czyli $f(x_{0}+h)-f(x_{0})$ ma dla $h<0$ inny znak niż dla $h>0,$ więc nie istnieje ekstremum w punkcie $x_{0}.$

Proste zagadnienia optymalizacyjne

Siatka prostopadłościennego pudełka wykonana z kwadratu o boku długości $a.$

Zagadnienie wyznaczania ekstremów funkcji występuje często w fizyce i technice. Oto przykład:

Pudełko o największej objętości

Problem

Z kwadratowego arkusza blachy o boku $a$ wycinane są przy wierzchołkach przystające kwadraty i po zagięciu brzegów tworzone jest prostopadłościenne pudełko. Jak otrzymać pudełko o największej objętości?

Rozwiązanie 1

Jeśli przez $x$ oznaczyć długość boku wyciętego kwadratu, to objętość $V$ pudełka będzie równa

$V(x)=x(a-2x)^{2},$

przy czym

$0\leqslant x\leqslant {\tfrac {1}{2}}a.$

Zadanie sprowadza się do znalezienia ekstremum funkcji $V$ w przedziale $[0,{\tfrac {1}{2}}a],$ przy czym wartości krańcowe reprezentują pudełko odpowiednio bez ścianek oraz bez podstawki, a więc o zerowej (minimalnej) objętości.

Pochodna

$V'(x)=(a-2x)(a-6x)$

zeruje się na tym przedziale w punktach $x_{0}:={\tfrac {a}{6}}$ oraz $x_{1}:={\tfrac {a}{2}}$ (w tym przypadku objętość jest zerowa). Ponieważ funkcja objętości jest dodatnia wewnątrz przedziału, 0 na jego końcach i ma we wnętrzu nie więcej niż jedno ekstremum lokalne, to ma ona dokładnie jedno maksimum, które jest zarazem lokalne i globalne (twierdzenie Rolle’a); osiągane jest ono w $x_{0}.$ Dlatego największa objętość pudełka wynosi

$V(x_{0})={\frac {2}{27}}a^{3}.$

Rozwiązanie 2

Wielkość $W(x):=4V(x)=ABC,\quad {}$ gdzie

$A:=4x$ oraz $B:=C:=a-2x$

są nieujemne, przyjmuje wartość maksymalną dla tego samego $x$ co $V(x).$ Ponieważ

$A+B+C=2a$

jest stałe i dodatnie, więc stała i dodatnia jest też średnia arytmetyczna nieujemnych liczb $A,B,C.$

$W(x)$ jest natomiast sześcianem ich średniej geometrycznej. Wiadomo, że średnia geometryczna liczb nieujemnych jest zawsze mniejsza lub równa od arytmetycznej, przy czym równość między tymi średnimi zajdzie tylko, gdy $A=B=C$ (zob. nierówności między średnimi potęgowymi), czyli gdy

$4x=a-2x,$

czyli dla

$x={\frac {a}{6}}.$

Zatem dla tej właśnie wartości $x,$ $V(x)$ przyjmuje wartość maksymalną:

$V\left({\frac {a}{6}}\right)={\frac {2}{27}}a^{3}.$

Koszt eksploatacji statku

Problem

Wiadomo, że koszt eksploatacji statku w ciągu godziny pływania wyraża się wzorem empirycznym $a+bv^{3},$ gdzie $v$ oznacza prędkość statku w węzłach (1 węzeł = 1 Mm/h ≈ 1,85 km/h), natomiast $a$ i $b$ są stałymi, które powinny być obliczone dla każdego statku z osobna (część stała kosztu $a$ pochodzi od amortyzacji i kosztów utrzymania załogi, a część $bv^{3}$ od kosztów paliwa). Przy jakiej prędkości statek przebędzie dowolną odległość z najmniejszymi kosztami?

Rozwiązanie

Przebycie 1 mili morskiej trwa 1/v godziny, więc kosztuje:

$f(v):={\tfrac {1}{v}}(a+bv^{3})=bv^{2}+{\tfrac {a}{v}}.$

Przyrównując pochodną $f'$ do zera, mamy:

$2bv-{\tfrac {a}{v^{2}}}=0,$ skąd $v={\sqrt[{3}]{\tfrac {a}{2b}}}.$

Ponieważ druga pochodna

$f''(v)=2b+2{\tfrac {a}{v^{3}}}>0,$

więc koszty rzeczywiście osiągną najmniejszą wartość dla znalezionej wartości $v.$

Funkcje określone na podzbiorach przestrzeni unormowanych

Pewne wyniki związane z istnieniem ekstremów, otrzymane dla funkcji argumentów rzeczywistych, przenoszą się na funkcje określone na podzbiorach przestrzeni unormowanych.

Paraboloida hiperboliczna – w pobliżu początku układu współrzędnych ma ona kształt podobny do siodła (zob. punkt siodłowy)

W dalszej części tego paragrafu przez $X$ rozumiana jest dowolna przestrzeń unormowana, zaś przez $D$ pewien jej otwarty podzbiór. Funkcja $f\colon D\to \mathbb {R}$ musi być różniczkowalna (w sensie Frécheta) w zbiorze $D.$ Przez zapis $f'(x_{0})$ lub $df(x_{0})$ rozumie się różniczkę funkcji $f,$ która jest odwzorowaniem liniowym i ciągłym przestrzeni $X$ o wartościach w $\mathbb {R} .$ Pochodna $n$-tego rzędu funkcji ($n$-krotnie różniczkowalnej) jest odwzorowaniem $n$-liniowym przestrzeni $X\times \ldots \times X$ o wartościach rzeczywistych i oznaczana jest przez $f^{(n)}(x_{0})$ lub $df^{n}(x_{0}).$

Podobnie jak dla funkcji rzeczywistych, warunkiem koniecznym istnienia ekstremum w punkcie $x_{0}\in D$ jest, aby wartość funkcji będącej różniczką w $x_{0}\in D$ wynosiła zero dla wszystkich punktów w pewnym otoczeniu $x_{0}$ $(f'(x_{0})\equiv 0).$ Punkt, w którym różniczka się zeruje (jest funkcją stale równą zero w pewnym otoczeniu $x_{0}$), nazywany jest punktem stacjonarnym.

Tak jak w przypadku funkcji jednej zmiennej, w punkcie stacjonarnym wcale nie musi być ekstremum. Na przykład dla funkcji $g\colon \mathbb {R} ^{2}\to \mathbb {R}$ danej wzorem $g(x,y)=xy,$ której wykresem jest paraboloida hiperboliczna, pochodne cząstkowe $g'_{x}(x,y)=x,\;g'_{y}(x,y)=y$ są jednocześnie równe zeru tylko w punkcie $(0,0),$ w którym $f(x,y)=0.$ Jednocześnie widać (por. rysunek obok), że w dowolnym otoczeniu zera funkcja przybiera zarówno wartości dodanie, jak i ujemne, a więc nie może być w nim ekstremum.

Definicje pomocnicze

Na potrzeby dalszych twierdzeń, konieczne będzie wprowadzenie kilku definicji:

Funkcjonał dwuliniowy $\varphi \colon X\times X\to \mathbb {R}$ jest nieujemny, niedodatni, dodatni, ujemny jeśli odpowiednio $\varphi (h,h)\geqslant 0,\;\varphi (h,h)\leqslant 0,\;\varphi (h,h)>0,\;\varphi (h,h)<0$ dla wszelkich $0\neq h\in X.$

Funkcjonał dwuliniowy $\varphi \colon X\times X\to \mathbb {R}$ jest

• dodatnio określony, jeśli

$\bigvee _{c>0}\bigwedge _{h\in X}\varphi (h,h)\geqslant c\|h\|^{2},$

• ujemnie określony, jeśli

$\bigvee _{c>0}\bigwedge _{h\in X}\varphi (h,h)\leqslant -c\|h\|^{2}.$

W szczególności, każda macierz kwadratowa może być interpretowana jako macierz funkcjonału dwuliniowego przestrzeni $X=\mathbb {R} ^{m}$ (por. macierz dodatnio określona). Prawdziwe jest twierdzenie, które mówi, że każdy dodatni (lub ujemny) funkcjonał dwuliniowy tej przestrzeni jest dodatnio określony (ujemnie określony). Do badania dodatniej (ujemnej) określoności macierzy służy kryterium Sylvestera.

Ekstrema a druga pochodna

Jeżeli funkcja $f$ jest dwukrotnie różniczkowalna w pewnym otoczeniu $E\subseteq D$ punktu $x_{0},$ przy czym $f'(x_{0})=0,$ a pochodna $f''$ jest ciągła w $x_{0},$ to

• jeżeli $f$ ma w $x_{0}$ minimum lokalne, to $f''(x_{0})$ jest nieujemna,
• jeżeli $f$ ma w $x_{0}$ maksimum lokalne, to $f''(x_{0})$ jest niedodatnia.

Warunek konieczny i wystarczający istnienia ekstremum

Niech, jak poprzednio, funkcja $f$ będzie dwukrotnie różniczkowalna w pewnym otoczeniu $U\subseteq D$ punktu $x_{0},$ przy czym $f'(x_{0})=0,$ a pochodna $f''$ jest ciągła w $x_{0}.$

• Jeżeli $f''(x_{0})$ jest dodatnio określona, to $f$ ma minimum lokalne właściwe w punkcie $x_{0}.$
• Jeżeli $f''(x_{0})$ jest ujemnie określona, to $f$ ma maksimum lokalne właściwe w punkcie $x_{0}.$

Funkcje określone na podzbiorach płaszczyzny

Ważnym przypadkiem są funkcje określone na podzbiorach $X=\mathbb {R} ^{2}.$ Przypadek ten zasługuje na wyróżnienie ponieważ funkcje tego typu szczególnie często pojawiają się w zastosowaniach. Korzystając z własności pochodnych cząstkowych takich funkcji można podać następujący algorytm badania istnienia ekstremów funkcji $f\colon D\to \mathbb {R} ,$ gdzie $D$ jest otwartym podzbiorem płaszczyzny. O funkcji $f$ wiadomo, że jest dwukrotnie różniczkowalna i jej druga pochodna jest ciągła.

1. Wyznaczamy wszystkie punkty $(x_{0},y_{0})\in D$ takie, że pochodne cząstkowe
   
   $\left\{{\begin{matrix}f'_{x}(x_{0},y_{0})=0\\f'_{y}(x_{0},y_{0})=0\end{matrix}}\right.$ (rozwiązując ten układ równań).
2. Dla każdego punktu z osobna badamy znak wyznacznika Hessego
   
   $\delta (x_{0},y_{0})=\left|{\begin{array}{l}f''_{xx}(x_{0},y_{0})&f''_{xy}(x_{0},y_{0})\\f''_{yx}(x_{0},y_{0})&f''_{yy}(x_{0},y_{0})\end{array}}\right|$
   
   Na mocy Twierdzenia Schwarza $f''_{xy}(x_{0},y_{0})=f''_{yx}(x_{0},y_{0}),$ więc:
   
   $\delta (x_{0},y_{0})=f''_{xx}(x_{0},y_{0})f''_{yy}(x_{0},y_{0})-(f''_{xy}(x_{0},y_{0}))^{2}.$
3. Jeżeli w danym punkcie $(x_{0},y_{0})$ wyznacznik $\delta (x_{0},y_{0})<0,$ to w tym punkcie nie ma ekstremum, jeśli $\delta (x_{0},y_{0})=0,$ to w pewnych przypadkach może istnieć ekstremum, a pewnych nie. I ostatecznie, jeżeli $\delta (x_{0},y_{0})>0,$ to istnieje ekstremum lokalne w tym punkcie, jeśli:

• $f''_{xx}(x_{0},y_{0})>0$ co dla $\delta (x_{0},y_{0})>0$ jest równoważne $f''_{yy}(x_{0},y_{0})>0,$ to jest to minimum lokalne,
• $f''_{xx}(x_{0},y_{0})<0$ co dla $\delta (x_{0},y_{0})>0$ jest równoważne $f''_{yy}(x_{0},y_{0})<0$ to jest to maksimum lokalne.

Przykład

Wykres funkcji $f(x,y)=2x^{3}-y^{3}+12x^{2}+27y$ z zaznaczonymi ekstremami lokalnymi i punktami siodłowymi

Znaleźć ekstrema funkcji

$f(x,y)=2x^{3}-y^{3}+12x^{2}+27y.$

Obliczamy pierwsze pochodne cząstkowe funkcji $f$ i przyrównujemy do zera:

$\left\{{\begin{matrix}f'_{x}(x,y)=0\Leftrightarrow 6x^{2}+24x=0\\f'_{y}(x,y)=0\Leftrightarrow -3y^{2}+27=0\end{matrix}}\right.$

Układ równań ma dokładnie 4 rozwiązania, którymi są punkty

$a=(0,3),\ b=(0,-3),\ c=(-4,-3),\ d=(-4,3),$

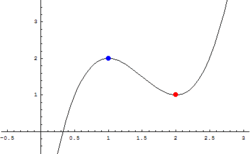
• $\delta (a)<0$ i $\delta (c)<0$ – zatem w tych punktach nie ma ekstremów (na wykresie zaznaczono je na pomarańczowo, są to tzw. punkty siodłowe funkcji $f$),
• $\delta (b)>0$ – w tym punkcie jest minimum lokalne (zaznaczono na czerwono),
• $\delta (d)>0$ – w tym punkcie jest maksimum lokalne (zaznaczono na zielono).

Funkcje uwikłane

W tej sekcji rozważane będą ekstrema funkcji $y(x),$ dla której nie znamy jednak bezpośredniej zależności $y$ od $x,$ mając jedynie równanie postaci $F(x,y)=0.$

Podobnie jak w poprzednim przypadku, o funkcji $F$ zakładamy, że jest dwukrotnie różniczkowalna w pewnym otwartym podzbiorze $D\subset \mathbb {R} ^{2}$ oraz $E$ jest zbiorem punktów $(x,y)$ obszaru, w których

$F(x,y)=0.$

Na mocy twierdzenia o funkcji uwikłanej, wzór

$y'(x)=-{\frac {F'_{x}(x,y)}{F'_{y}(x,y)}},$

gdzie $y=y(x),$ a w konsekwencji także

$y''=-{\frac {F''_{xx}(F'_{y})^{2}-2F''_{xy}F'_{x}F'_{y}+F''_{yy}(F'_{x})^{2}}{(F'_{y})^{3}}}$

pozwala wyznaczyć ekstrema funkcji $y$ uwikłanej w równaniu $F(x,y)=0$. W tym celu należy wyznaczyć punkty, w których

$F(x,y)=0,y'=0,y''\neq 0.$

Dwa ostatnie warunki równoważne są poniższym, tj.

$F'_{x}=0,-{\frac {F''_{xx}}{F'_{y}}}\neq 0.$

Przykład

Znaleźć ekstrema funkcji $y,$ określonej równaniem

$F(x,y)=x^{2}-2xy-3y^{2}+4=0.$

Ponieważ

$F'_{x}(x,y)=2x-2y=0,$

tylko gdy $x=y,$ więc wstawiając to do równania

$F(x,y)=0$

otrzymujemy jako jedyne rozwiązania punkty $(1,1),(-1,-1).$

Ponieważ

$F'_{y}(x,y)=-2x-6y$

oraz

$F''_{xx}(x,y)=2,$

zatem w punkcie $(1,1)$ druga pochodna

$y''(-1)=-{\tfrac {2}{-8}}={\tfrac {1}{4}}>0,$

czyli w tym punkcie jest minimum lokalne, natomiast w punkcie $(-1,-1),$

$y''(-1)={\tfrac {-2}{8}}=-{\tfrac {1}{4}}<0,$

czyli w tym punkcie jest maksimum lokalne funkcji $y.$

Rachunek wariacyjny

Na czerwono zaznaczono fragment cykloidy – brachistochronę. Punkt materialny stacza się od punktu $A$ do punktu $B$ w najkrótszym czasie właśnie po tej krzywej.

Ważnymi obiektami matematycznymi są te funkcjonały, które danej funkcji przypisują liczbę rzeczywistą, np. długość łuku jej wykresu. Przestrzeń funkcyjna jest przestrzenią unormowaną, opisywaną w jednej z wcześniejszych sekcji, jednak badanie ekstremów tych funkcjonałów jest szczególnie istotne ze względu na zastosowania w fizyce i technice – przykładowo jeśli funkcja będąca argumentem funkcjonału opisuje kształt śmigła samolotu, a wartości funkcjonału opisują wydajność śmigła, to znalezienie globalnego maksimum jest równoważne wyliczeniu jaki kształt śmigła zapewni największą wydajność.

Badania funkcjonałów zapoczątkował Leonard Euler. Klasycznym problemem, prowadzącym do znalezienia ekstremów pewnego funkcjonału jest zagadnienie brachistochrony, postawione w 1696 przez Jana Bernoulliego w periodyku Acta Eroditorium. Sprowadza się ono do znalezienia takiej krzywej łączącej dwa punkty $A$ i $B,$ aby ciało staczające się po niej od punktu $A$ do $B$ pokonało tę drogę w najkrótszym czasie.

Ekstrema mocne i słabe

Szukając lokalnych ekstremów funkcjonałów konieczne jest zdefiniowanie przestrzeni topologicznej. Najprościej zrobić to konstruując bazę coraz węższych otoczeń wokół każdego punktu dziedziny. Rozsądnie jest przyjąć, że ciąg funkcji należących do coraz węższych otoczeń powinien zbiegać do funkcji $f$ odpowiadającej otaczanemu punktowi, jednak nie jest oczywiste, czy także pochodne tych funkcji muszą zbiegać do pochodnej $f.$ Jeśli przyjmiemy, że tak, to mówimy o tzw. ekstremum mocnym, jeśli natomiast dopuszczamy dowolne wartości pochodnej, o ekstremum słabym. Każde ekstremum mocne jest szczególnym przypadkiem słabego, odwrotnie – niekoniecznie.

Przykład – równania Eulera-Lagrange’a

Rachunek wariacyjny bada ekstrema funkcjonałów, często zadanych w postaci całek. W mechanice klasycznej ważne są równania, pozwalające na znajdowanie torów cząstek $q_{k},$ jeśli znana jest funkcja $L$ (lagranżjan), opisująca ten układ. Równania te zostały wprowadzone w 1750 roku przez Leonharda Eulera oraz Josepha Louisa Lagrange’a i zwane są dziś nazwiskami ich odkrywców. Równania Eulera-Lagrange’a mają ścisły związek z metodami rachunku wariacyjnego.

Formalnie, o funkcji $L$ zakłada się, że jest określona na $\mathbb {R} ^{2n+1}$ oraz jest dwukrotnie różniczkowalna w sposób ciągły. Dalej, o funkcji

$[a,b]\ni t\mapsto q(t)=(q_{1}(t),\dots ,q_{n}(t))\in \mathbb {R} ^{n}$

zakłada się, że jest funkcją o wartościach wektorowych, dwukrotnie różniczkowalną w sposób ciągły. W celu wyznaczenia toru cząstki, określa się funkcjonał

$F(q)=\int \limits _{a}^{b}L\left(t,q_{1}(t),\dots ,q_{n}(t),{\frac {dq_{1}}{dt}}(t),\dots ,{\frac {dq_{n}}{dt}}(t)\right)dt.$

Ekstremów tego funkcjonału szuka się w klasie funkcji dwukrotnie różniczkowalnych, przyjmujących na końcach przedziału $[a,b]$ wartości

$q_{1}(a),q_{1}(b),\dots ,q_{n}(a),q_{n}(b).$

Jest to problem z tzw. ustalonym brzegiem. Okazuje się, że funkcje $q_{i},$ dla których funkcjonał $F$ przyjmuje ekstremum, spełniają układ równań różniczkowych cząstkowych, zwanych równaniami Eulera-Lagrange’a, postaci:

${\frac {\partial L}{\partial q_{k}}}-{\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {q}}_{k}}}\right)=0,\quad 1\leqslant k\leqslant n,$

gdzie:

${\dot {q}}_{k}={\frac {dq_{k}}{dt}}.$

Ekstrema warunkowe

W matematyce i fizyce zachodzi często potrzeba badania ekstremów funkcji przy pewnych dodatkowych warunkach. Chcąc np. znaleźć odległość punktu $(x_{0},y_{0},z_{0})\in \mathbb {R} ^{3}$ od hiperpowierzchni zadanej równaniem $g(x,y,z)=0$ należy zbadać minima funkcji

$f(x,y,z)=(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}$

przy warunku dodatkowym

$g(x,y,z)=0.$

W paragrafie tym podamy ogólną definicję ekstremum warunkowego (inaczej: związanego) i ogólne wyniki tej teorii, badanie ekstremów warunkowych funkcji tylko dwóch zmiennych zostanie omówione w następnym ustępie.

Jeśli $X$ jest przestrzenią topologiczną, $Y$ przestrzenią liniową, $G\colon X\to Y$ oraz $M=\{x\in X\colon G(x)=0\},$ to mówimy, że funkcja $f\colon X\to \mathbb {R}$ ma w punkcie $x_{0}\in M$ minimum (maksimum) lokalne przy warunku $M$ (albo związane zbiorem $M$), jeśli istnieje otoczenie $U$ punktu $x_{0}$ takie, że $f(x_{0})\leqslant f(x),$ względnie $f(x_{0})\geqslant f(x)$ dla $x\in U\cap M.$

Warunek konieczny istnienia ekstremum warunkowego

W dalszym ciągu będziemy zakładali spełnienie założeń twierdzenia Lusternika, tj.

1. $X$ i $Y$ są przestrzeniami Banacha,
2. $G\colon X\to Y$ jest różniczkowalne w sposób ciągły w pewnym otoczeniu punktu $x_{0}\in X,$
3. $x_{0}\in X$ jest punktem regularnym zbioru $M=G^{-1}(\{0\}),$ tj. $G'(x_{0})$ jest suriekcją $X$ na $Y,$
4. $X_{1}:=(G'(x_{0}))^{-1}(\{0\}),$ to znaczy $X_{1}$ jest jądrem $G'(x_{0}),$
5. $X=X_{1}\oplus X_{2}$ (rozkład przestrzeni $X$ na topologiczną sumę prostą).

Niech $f$ będzie funkcją określoną na otwartym podzbiorze $U$ przestrzeni Banacha $X$ o wartościach w $\mathbb {R}$ oraz niech $x_{0}\in X$ będzie punktem regularnym zbioru $M=G^{-1}(0).$ Jeżeli funkcja $f$ jest różniczkowalna w punkcie $x_{0}$ i ma w tym punkcie ekstremum warunkowe, to

$f'(x_{0})x_{1}=0$     dla każdego $x_{1}\in X_{1}.$

W praktyce, często wykorzystywanym faktem do badania ekstremów warunkowych jest tzw. drugie twierdzenie Lusternika, mówiące o tym, że jeżeli spełnione są założenia twierdzenia Lusternika i funkcja $f,$ określona jak wyżej, jest różniczkowalna w punkcie $x_{0}\in M$ i ma w tym punkcie ekstremum warunkowe (związane warunkiem $M$), to istnieje funkcjonał liniowy $\Lambda \in Y^{\star }$ taki, że

$f'(x_{0})=\Lambda \circ G'(x_{0}).$

Funkcjonał $\Lambda$ nazywany jest funkcjonałem Lagrange’a i ma ścisły związek z metodą szukania ekstremów warunkowych, zwaną metodą mnożników Lagrange’a, opisaną dalej.

Warunki wystarczające istnienia ekstremum warunkowego

W dalszym ciągu, podtrzymując powyższe założenia i zakładając dodatkowo, że funkcje $f$ i $G$ są dwukrotnie różniczkowalne w sposób ciągły w pewnych otoczeniach punktu $x_{0},$ można sformułować warunek wystarczający istnienia ekstremum warunkowego. Mianowicie, jeżeli istnieje funkcjonał liniowy $\Lambda \in Y^{\star }$ taki, że

$f'(x_{0})=\Lambda \circ G'(x_{0})$

oraz

$(f''(x_{0})-\Lambda \circ G''(x_{0}))(h)$

jest dodatnio (ujemnie) określona dla $h\in X_{1}=\ker G'(x_{0}),$ to funkcja $f$ ma w punkcie $x_{0}$ minimum (maksimum) warunkowe.

Twierdzenie to można udowodnić korzystając z twierdzenia Lusternika i odpowiednio wykorzystując twierdzenia Taylora. Daje się ono łatwo uogólnić na przypadek pochodnych wyższych rzędów – w tym przypadku dodatkowo zakłada się, że odwzorowania $f$ i $G$ są różniczkowalne $2n$ razy w sposób ciągły w pewnym otoczeniu punktu $x_{0}.$ Wówczas, jeżeli istnieje funkcjonał $\Lambda \in Y^{\star }$ taki, że

$f^{(k)}(x_{0})=\Lambda \circ G^{(k)}(x_{0})$

dla $k=1,2,\dots ,2n-1$ oraz odwzorowanie

$\left(f^{(2n)}(x_{0})-\Lambda \circ G^{(2n)}(x_{0})\right)(h)$

jest dodatnio (ujemnie) określona dla $h\in X_{1},$ to funkcja $f$ ma w punkcie $x_{0}$ minimum (maksimum) warunkowe.

Ekstrema warunkowe w $\mathbb {R} ^{n}$

Badanie ekstremów warunkowych przekształceń dowolnych przestrzeni Banacha jest rzeczą trudną. Już samo spełnienie założeń twierdzenia Lusternika może okazać się niemożliwe, gdyż nie każdą przestrzeń unormowaną da się rozłożyć na topologiczną sumę prostą jej podprzestrzeni. Duża część zagadnień praktycznych sprowadza się do badania ekstremów warunkowych w przypadku gdy $X=\mathbb {R} ^{n},\;Y=\mathbb {R} ^{m},\;n\geqslant m,$ a odwzorowanie $G\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}$ reprezentowane jest przez układ $m$ funkcji o $n$ zmiennych, tj. $G=(G_{1},\dots ,G_{m}).$

Szukanie ekstremów warunkowych funkcji $f\colon \mathbb {R} ^{n}\to \mathbb {R} ,$ będących zarazem punktami regularnymi, sprowadza się do rozwiązania układu równań operatorowych

$\left\{{\begin{array}{l}f'(x)=\Lambda \circ G'(x)\\G(x)=0\end{array}}\right.$

gdzie $\Lambda \in (\mathbb {R} ^{m})^{\star }.$ Wiadomo, że każdy taki funkcjonał $\Lambda$ jest reprezentowany przez układ $m$ liczb rzeczywistych $\lambda _{1},\dots ,\lambda _{m}$ a pochodna $G'(x)$ jest macierzą wymiaru $m\times n$ rzędu $m$. Układ równań operatorowych sprowadza się więc do układu $m+n$ równań skalarnych:

$\left\{{\begin{array}{l}{\frac {\partial f(x)}{\partial x_{j}}}=\sum _{i=1}^{m}\lambda _{i}{\frac {\partial G_{i}(x)}{\partial x_{j}}},\;j=1,\dots ,n\\G_{k}(x_{1},\dots ,x_{n})=0,\;k=1,\dots ,m\end{array}}\right.$

gdzie $x=(x_{1},\dots ,x_{n})$ o $n+m$ zmiennych $\lambda _{i},x_{k},\;i\leqslant m,k\leqslant n.$ Wszystkie punkty, w których funkcja może przyjmować ekstrema warunkowe, należą do zbioru rozwiązań tego układu równań. Liczby $\lambda _{i}$ spełniają tylko rolę pomocniczą i nazywane są często mnożnikami Lagrange’a. Po znalezieniu punktów spełniających warunek konieczny dla ekstremum, należy odwołać się do warunku wystarczającego, tj. zbadać dodatnią (ujemną określoność)

$f''(x)-\Lambda \circ G''(x)$

dla

$h\in X_{1}=\ker G'(x_{0}),$

co sprowadza się do badania formy kwadratowej

$\sum _{i,j=1}^{n}\left({\frac {\partial ^{2}f(x)}{\partial x_{i}\partial x_{j}}}-\sum _{k=1}^{m}\lambda _{k}{\frac {\partial ^{2}G_{k}(x)}{\partial x_{j}\partial x_{j}}}\right)h_{i}h_{j},$

gdzie:

$h\in X_{1},h=(h_{1},\dots ,h_{n}).$

Warunek $h\in X_{1}$ jest równoważny równaniu

$G'(x)h=0,$

które w postaci macierzowej przybiera formę

$\sum _{i=1}^{n}{\frac {\partial G_{k}(x)}{\partial x_{i}}}h_{i}=0,\;k=1,2,\dots ,m.$

Do badania określoności tej macierzy można stosować kryterium Sylvestera.

W praktyce, gdy $X=\mathbb {R} ^{2},Y=\mathbb {R}$ wprowadzamy funkcję pomocniczą

$F(x,y)=f(x,y)+\lambda G(x,y)$

i szukamy dla niej warunków koniecznych na istnienie jej ekstremów, jako funkcji dwóch zmiennych, tj. rozwiązaniu układu równań $F'_{x}=0,F'_{y}=0,$ a następnie wyrugowaniu z tego układu równań czynnika nieoznaczonego $\lambda .$
Do otrzymanego warunku dołączamy warunek $G(x,y)=0.$ Równoważnie, wszystkie punkty, które mogą być ekstremami warunkowymi można wyznaczyć z układu równań

$\left\{{\begin{array}{l}{\frac {D(f,G)}{D(x,y)}}=0\\G(x,y)=0\end{array}}\right.$

gdzie ${\tfrac {D(f,G)}{D(x,y)}}$ oznacza jakobian funkcji $f$ i $G.$

Przykład – ekstrema funkcji na okręgu

Wykresem funkcji $f(x,y)=x+y$ jest płaszczyzna. W przestrzeni trójwymiarowej, równanie $x^{2}+y^{2}=1$ opisuje walec (u którego podstawy, na płaszczyźnie $xy$ leży okrąg jednostkowy). Szukanie ekstremów warunkowych sprowadza się w tym wypadku do badania punktów ekstremalnych części wspólnej walca i płaszczyzny.

Ilustracją zastosowania metody mnożników Lagrange’a jest problem wyznaczenia ekstremów funkcji:

$f(x,y)=x+y$

na kole jednostkowym, tj. przy warunku

$x^{2}+y^{2}=1.$

Zatem funkcja $G$ jest postaci

$G(x,y)=x^{2}+y^{2}-1,$

a więc funkcja $F$ wyraża się wzorem:

$F(x,y)=f(x,y)+\lambda G(x,y)=x+y+\lambda (x^{2}+y^{2}-1).$

Wszystkie punkty, które mogą być ekstremami warunkowymi są rozwiązaniami układu równań

$\left\{{\begin{array}{l}F'_{x}(x,y)=1+2\lambda x&=0\\F'_{y}(x,y)=1+2\lambda y&=0\\G(x,y)=x^{2}+y^{2}-1&=0\end{array}}\right.$

Podstawiając $x=y,x\neq 0$ do pierwszego równania uzyskujemy: $\lambda =-{\tfrac {1}{2x}}.$ Stosując podobne podstawienie do trzeciego równania, dostaje się warunek $2x^{2}=1,$ skąd wynika $x=\pm {\tfrac {\sqrt {2}}{2}}.$ Funkcja $f$ może zatem przyjmować ekstrema tylko w punktach $\left(-{\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}}\right),\left({\tfrac {\sqrt {2}}{2}},{\tfrac {\sqrt {2}}{2}}\right).$ Ponieważ okrąg jest zbiorem domkniętym i ograniczonym (czyli zwartym), więc na mocy twierdzenia Weierstrassa, funkcja $f$ osiąga w tych punktach ekstrema (warunkowe):

• minimum warunkowe: $f\left(-{\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}}\right)=-{\sqrt {2}},$
• maksimum warunkowe: $f\left({\tfrac {\sqrt {2}}{2}},{\tfrac {\sqrt {2}}{2}}\right)={\sqrt {2}}.$

Warto zauważyć, że funkcja $f,$ określona na całej płaszczyźnie (bez dodatkowego warunku) nie ma ekstremów.

Przykład – problem maksymalnej entropii

Problem polega na znalezieniu dyskretnego rozkładu zmiennej losowej maksymalizującego entropię. Funkcja entropii prawdopodobieństw $p_{1},\dots ,p_{n}$ wyraża się wzorem

$f(p_{1},p_{2},\dots ,p_{n})=-\sum _{k=1}^{n}p_{k}\log _{2}p_{k}.$

Oczywiście, suma prawdopodobieństw $p_{1},\dots ,p_{n}$ jest równa jeden, więc warunek na $G$ przyjmuje postać

$G(p_{1},p_{2},\dots ,p_{n})=\sum _{k=1}^{n}p_{k}-1.$

Stosując metodę mnożników Lagrange’a, dostajemy układ $n$ równań:

${\frac {\partial }{\partial p_{k}}}(f(p_{1},p_{2},\dots ,p_{n})+\lambda (G(p_{1},p_{2},\dots ,p_{n})-1))=0,\quad 1\leqslant k\leqslant n,$

który sprowadza się do układu

${\frac {\partial }{\partial p_{k}}}\left(-\sum _{k=1}^{n}p_{k}\log _{2}p_{k}+\lambda \left(\sum _{k=1}^{n}p_{k}-1\right)\right)=0,\quad 1\leqslant k\leqslant n.$

Różniczkując każde równanie $n$-krotnie, powyższy układ sprowadza się do poniższego:

$-\left({\frac {1}{\ln 2}}+\log _{2}p_{k}\right)+\lambda =0,\quad 1\leqslant k\leqslant n.$

Z powyższego wynika, że wszystkie prawdopodobieństwa są równe, tj. $p_{1}=\ldots =p_{n},$ a ponieważ ich suma jest równa jeden, wynika stąd, że dla dowolnego $1\leqslant k\leqslant n{:}$

$p_{k}={\frac {1}{n}}.$

Gradacyjna analiza odpowiedniości

Ciekawym praktycznym zastosowaniem ekstremum lokalnego w przestrzeni par permutacji jest algorytm statystyczny, zwany gradacyjną analizą odpowiedniości (Grade Correspondence Analysis, GCA).

Algorytm ma na celu przekształcenie badanych nominalnych cech statystycznych w cechy porządkowe tak, aby korelacja rangowa pomiędzy nimi w zbiorze uczącym była maksymalna.

Algorytm GCA był stosowany m.in. do tabeli, w której wiersze odpowiadają okręgom wyborczym, kolumny partiom politycznym, a liczby w komórkach macierzy liczbie głosów oddanych na poszczególne partie w poszczególnych okręgach GCA rozmieściło zarówno okręgi wyborcze, jak i partie na skali, która po zbadaniu okazała się odpowiadać continuum lewica-prawica.

Ściśle: danymi wejściowymi jest tzw. macierz kontyngencji, której wiersze odpowiadają możliwym wartościom (tzw. etykietom) pewnej nominalnej cechy statystycznej (zwanej zmienną wierszową), a kolumny możliwym wartościom innej cechy nominalnej (zwanej zmienną kolumnową). Wartości elementów macierzy reprezentują liczebność obserwacji w próbie, dla których rozważane dwie cechy mają wartości przypisane do danego wiersza i kolumny.

Celem algorytmu jest znalezienie takiej permutacji wierszy i kolumn macierzy (czyli etykiet zmiennych wierszowej i kolumnowej), aby współczynnik rho Spearmana dla powstałego rozkładu dwuwymiarowego był największy. Odpowiada to znalezieniu takiego uszeregowania etykiet zmiennych nominalnych, aby powstałe w ten sposób zmienne porządkowe wykazywały możliwie dużą zależność statystyczną w sensie korelacji rangowej.

GCA jest algorytmem iteracyjnym, który wielokrotnie startując od losowych permutacji wierszy i kolumn macierzy, dochodzi do różnych lokalnych maksimów rho Spearmana. Maksima są lokalne w tym sensie, że aby uzyskać większą wartość trzeba zmienić jednocześnie kolejność wierszy i kolumn macierzy. Zmiana wyłącznie kolejności wierszy lub wyłącznie kolejności kolumn nie da wyższej wartości rho.

Zobacz też

• funkcje minimum i maksimum
• twierdzenie Lagrange’a
• twierdzenie Rolle’a

Bibliografia

• Michał Krych: Analiza matematyczna dla ekonomistów. Wyd. I. Warszawa: Wydawnictwa Uniwersytetu Warszawskiego, 2010. ISBN 978-83-235-0776-5.

Literatura dodatkowa

• Grigorij Michajłowicz Fichtenholz: Rachunek różniczkowy i całkowy, t. 1. Warszawa: Państwowe Wydawnictwo Naukowe, 1966.brak strony w książce
• Witold Kołodziej: Analiza matematyczna. Warszawa: PWN, 1979.brak strony w książce
• Teresa Kowalczyk, Elżbieta Pleszczyńska, Fred (red.) Ruland: Grade Models and Methods for Data Analysis with Applications for the Analysis of Data Populations. Berlin Heidelberg New York: seria: Studies in Fuzziness and Soft Computing, vol. 151, Springer Verlag, 2004, s. 477.
• Franciszek Leja: Rachunek różniczkowy i całkowy. Warszawa: PWN, 1976.brak strony w książce
• Krzysztof Maurin: Analiza – Część I – Elementy. Warszawa: PWN, 1976. ISBN 978-83-01-09939-8.brak strony w książce