Płaszczyzna Fana

Płaszczyzna Fana – struktura geometryczna. Nazwana na cześć włoskiego matematyka Gina Fana.

Jest to zbiór złożony z siedmiu elementów zwanych punktami, w którym wyróżniono rodzinę siedmiu podzbiorów zwanych prostymi, spełniających następujące warunki:

• każde dwie różne proste mają dokładnie jeden punkt wspólny
• każde dwa różne punkty należą do dokładnie jednej prostej

Fano Plane (7 points and 7 lines)

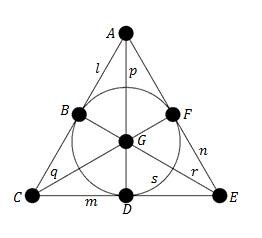
Stosując oznaczenia z rysunku, jest to zbiór {A,B,C,D,E,F,G}, w którym wyróżniono rodzinę następujących podzbiorów:

• {A,B,C}, {A,F,E}, {C,D,E} przedstawione jako boki trójkąta odpowiednio l, n, m
• {A,G,D}, {C,G,F}, {E,G,B} przedstawione jako wysokości trójkąta odpowiednio p, q, r
• {B,D,F} przedstawiony jako okrąg s

Własności

• każda prosta składa się z trzech różnych punktów
• każdy punkt należy do trzech różnych prostych

Płaszczyzna Fana została skonstruowana w celu wykazania niezależności aksjomatu Fana od pozostałych aksjomatów płaskiej geometrii rzutowej.