Problem ucztujących kryptografów

Problem ucztujących kryptografów – problem postawiony w 1988 przez Davida Chauma. Polega na znalezienie schematu bezpiecznego obliczenia funkcji OR przez kilka niezależnych stron.

Opis klasyczny problemu

Trzech kryptografów spotyka się na kolacji w restauracji. Kelner informuje ich, że rachunek został już opłacony przez anonimową osobę. Mógł to być jeden z ucztujących kryptografów bądź agencja NSA. Kryptografowie chcą się dowiedzieć czy sponsorem był któryś z nich, lecz żaden nie chce zdradzić czy zapłacił.

Opis abstrakcyjny problemu

Każda z osób posiada swój własny tajny bit (jeśli opłaciła to $1,$ w przeciwnym wypadku $0$). Wszyscy chcą poznać OR wszystkich tych bitów, ale nikt nie chce zdradzić swojego bitu.

Rozwiązanie Chauma

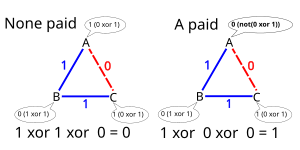
Dining Cryptographers network (DC-net) to schemat zaproponowany przez Davida Chauma.

Każda para kryptografów ustala sobie tajny bit (np. rzucając monetę). Następnie każdy kryptograf wykonuje XOR tajnych bitów ustalonych z pozostałymi. Jeśli dany kryptograf opłacił rachunek, musi otrzymany wynik zanegować. Następnie wszyscy kryptografowie ujawniają swoje wyniki. Jeśli XOR wszystkich trzech wyników jest równy $0$ to rachunek został opłacony przez NSA, jeśli $1$ to przez jednego z kryptografów. Fakt ten wynika z prostych własności funkcji XOR.

Problem można uogólnić na przypadek gdy mamy $n$ osób. Schemat postępowania wygląda analogicznie. Każda para ustala tajny bit. Następnie każda osoba wykonuje XOR wszystkich tajnych bitów ustalonych z pozostałymi i neguje wynik jeśli opłaciła rachunek. Wyniki są ujawniane. XOR tych wyników to wynik ostateczny.

Krytyka rozwiązania Chauma

Schemat Chauma jest rozwiązaniem niepełnym, gdyż oblicza de facto XOR tajnych bitów, a nie OR. Mianowicie, jeśli parzyście wiele osób zapłaci za rachunek to wynik ostateczny będzie niepoprawny: $0.$

Schemat jest również nieodporny na oszustwa (któryś z kryptografów, fałszując wynik swojej operacji XOR, fałszuje wynik ostateczny).

Dla dużych $n$ schemat staje się złożony obliczeniowo bo każda para osób musi ustalać sobie tajny bit.

Rozwiązanie optymalne

Anonymous Veto network (AV-net) to lepsze rozwiązanie. Pozwala ustalić, czy ktokolwiek z grupy osób zawetował, nie ujawniając tożsamości wetujących (jest to zatem faktyczne obliczenie funkcji OR). Schemat jest ponadto odporny na fałszerstwa (gdyż wymaga przedstawienia dowodu z wiedzą zerową przez każdego uczestnika).