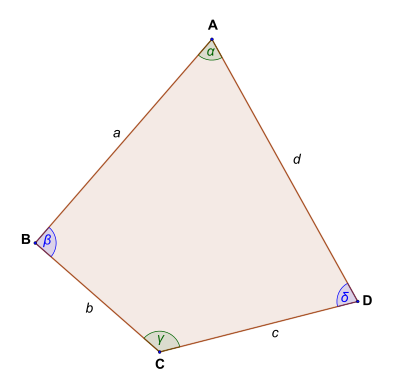
Czworokąt ABCD Twierdzenie Bretschneidera – twierdzenie geometryczne pozwalające obliczyć pole powierzchni dowolnego czworokąta znając jedynie długości jego boków oraz miary jego kątów. Zostało ono udowodnione niezależnie w 1842 roku przez Carla Bretschneidera [1] [2] oraz przez F. Strehlkego[2] [3] .
Niech dany będzie dowolny czworokąt ABCD o bokach długości
a
,
{\displaystyle a,}
b
,
{\displaystyle b,}
c
{\displaystyle c}
d
,
{\displaystyle d,}
α
,
{\displaystyle \alpha ,}
β
,
{\displaystyle \beta ,}
γ
{\displaystyle \gamma }
δ
.
{\displaystyle \delta .}
s
=
a
+
b
+
c
+
d
2
.
{\displaystyle s={\frac {a+b+c+d}{2}}.}
Wtedy pole tego czworokąta wyraża się przez[4]
S
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
a
b
c
d
cos
2
α
+
γ
2
.
{\displaystyle S={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}{\frac {\alpha +\gamma }{2}}}}.}
Przypadek, gdy czworokąt ABCD nie jest wypukły. Na początek zauważmy, że w twierdzeniu nie jest istotne, którą parę przeciwległych kątów –
α
{\displaystyle \alpha }
γ
,
{\displaystyle \gamma ,}
β
{\displaystyle \beta }
δ
{\displaystyle \delta }
cos
2
β
+
δ
2
=
cos
2
2
π
−
(
α
+
γ
)
2
=
cos
2
(
π
−
α
+
γ
2
)
=
(
−
cos
α
+
γ
2
)
2
=
cos
2
α
+
γ
2
.
{\displaystyle {\begin{aligned}\cos ^{2}{\frac {\beta +\delta }{2}}&=\cos ^{2}{\frac {2\pi -(\alpha +\gamma )}{2}}\\&=\cos ^{2}\left(\pi -{\frac {\alpha +\gamma }{2}}\right)\\&=\left(-\cos {\frac {\alpha +\gamma }{2}}\right)^{2}\\&=\cos ^{2}{\frac {\alpha +\gamma }{2}}.\end{aligned}}}
Oznaczmy pole czworokąta symbolem
S
.
{\displaystyle S.}
S
=
S
△
A
D
B
+
S
△
B
D
C
=
1
2
a
d
sin
α
+
1
2
b
c
sin
γ
.
{\displaystyle {\begin{aligned}S&=S_{\triangle ADB}+S_{\triangle BDC}\\&={\frac {1}{2}}ad\sin \alpha +{\frac {1}{2}}bc\sin \gamma .\end{aligned}}}
(1)
Zauważmy, że wzór ten działa zarówno, gdy czworokąt ABCD jest wypukły, jak i gdy jest wklęsły: przypuśćmy, że kąt
γ
{\displaystyle \gamma }
(1) przyjmuje postać
S
=
S
△
A
D
B
−
S
△
B
D
C
.
{\displaystyle S=S_{\triangle ADB}-S_{\triangle BDC}.}
Ale pole trójkąta BDC to
S
△
B
D
C
=
1
2
b
c
sin
(
2
π
−
γ
)
=
1
2
b
c
sin
(
−
γ
)
=
−
1
2
b
c
sin
γ
,
{\displaystyle S_{\triangle BDC}={\frac {1}{2}}bc\sin {(2\pi -\gamma )}={\frac {1}{2}}bc\sin(-\gamma )=-{\frac {1}{2}}bc\sin \gamma ,}
co ostatecznie daje ponownie wzór (1) .
Przemnażając wzór (1) przez 2 i podnosząc obustronnie do kwadratu, otrzymujemy
4
S
2
=
(
a
d
)
2
sin
2
α
+
(
b
c
)
2
sin
2
γ
+
2
a
b
c
d
sin
α
sin
γ
.
{\displaystyle 4S^{2}=(ad)^{2}\sin ^{2}\alpha +(bc)^{2}\sin ^{2}\gamma +2abcd\sin \alpha \sin \gamma .}
(2)
Z twierdzenia cosinusów zastosowanego do trójkątów ABD i BCD otrzymujemy
|
B
D
|
2
=
b
2
+
c
2
−
2
b
c
cos
γ
|
B
D
|
2
=
a
2
+
d
2
−
2
a
d
cos
α
.
{\displaystyle {\begin{aligned}|BD|^{2}&=b^{2}+c^{2}-2bc\cos \gamma \\|BD|^{2}&=a^{2}+d^{2}-2ad\cos \alpha .\end{aligned}}}
Łącząc powyższe równości otrzymujemy
a
2
+
d
2
−
b
2
−
c
2
=
2
a
d
cos
α
−
2
b
c
cos
γ
.
{\displaystyle a^{2}+d^{2}-b^{2}-c^{2}=2ad\cos \alpha -2bc\cos \gamma .}
Podnosząc równość do kwadratu i dzieląc przez 4, otrzymujemy:
1
4
(
a
2
+
d
2
−
b
2
−
c
2
)
2
=
(
a
d
)
2
cos
2
α
+
(
b
c
)
2
cos
2
γ
−
2
a
b
c
d
cos
α
cos
γ
.
{\displaystyle {\frac {1}{4}}(a^{2}+d^{2}-b^{2}-c^{2})^{2}=(ad)^{2}\cos ^{2}\alpha +(bc)^{2}\cos ^{2}\gamma -2abcd\cos \alpha \cos \gamma .}
(3)
Dodając stronami równania (2) i (3) oraz korzystając z tożsamości trygonometrycznych (jedynki trygonometrycznej, cosinusa sumy kątów oraz cosinusa podwojonego kąta), otrzymujemy kolejno:
4
S
2
+
1
4
(
a
2
+
d
2
−
b
2
−
c
2
)
2
=
(
a
d
)
2
cos
2
α
+
(
b
c
)
2
cos
2
−
2
a
b
c
d
cos
α
cos
γ
+
(
a
d
)
2
sin
2
α
+
(
b
c
)
2
sin
2
+
2
a
b
c
d
sin
α
sin
γ
=
(
a
d
)
2
+
(
b
c
)
2
−
2
a
b
c
d
(
cos
α
cos
γ
−
sin
α
sin
γ
)
=
(
a
d
)
2
+
(
b
c
)
2
−
2
a
b
c
d
cos
(
α
+
γ
)
=
(
a
d
)
2
+
(
b
c
)
2
−
2
a
b
c
d
cos
(
2
⋅
α
+
γ
2
)
=
(
a
d
)
2
+
(
b
c
)
2
−
2
a
b
c
d
(
2
cos
2
(
α
+
γ
2
)
−
1
)
=
(
a
d
+
b
c
)
2
−
4
a
b
c
d
cos
2
(
α
+
γ
2
)
.
{\displaystyle {\begin{aligned}4S^{2}+{\frac {1}{4}}(a^{2}+d^{2}-b^{2}-c^{2})^{2}&=(ad)^{2}\cos ^{2}\alpha +(bc)^{2}\cos ^{2}-2abcd\cos \alpha \cos \gamma +(ad)^{2}\sin ^{2}\alpha +(bc)^{2}\sin ^{2}+2abcd\sin \alpha \sin \gamma \\&=(ad)^{2}+(bc)^{2}-2abcd(\cos \alpha \cos \gamma -\sin \alpha \sin \gamma )\\&=(ad)^{2}+(bc)^{2}-2abcd\cos(\alpha +\gamma )\\&=(ad)^{2}+(bc)^{2}-2abcd\cos \left(2\cdot {\frac {\alpha +\gamma }{2}}\right)\\&=(ad)^{2}+(bc)^{2}-2abcd\left(2\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)-1\right)\\&=(ad+bc)^{2}-4abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).\end{aligned}}}
Przemnażając obie strony przez 4 i przenosząc jeden ze składników sumy na drugą stronę, równość przyjmuje postać
16
S
2
=
4
(
a
d
+
b
c
)
2
−
(
a
2
+
d
2
−
b
2
−
c
2
)
2
−
16
a
b
c
d
cos
2
(
α
+
γ
2
)
.
{\displaystyle 16S^{2}=4(ad+bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}-16abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).}
Zapisując wyrażenie
4
(
a
d
+
b
c
)
2
−
(
a
2
+
d
2
−
b
2
−
c
2
)
2
{\displaystyle 4(ad+bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}}
jako
(
2
a
d
+
2
b
c
)
2
−
(
a
2
+
d
2
−
b
2
−
c
2
)
2
{\displaystyle (2ad+2bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}}
oraz korzystając z wzorów skróconego mnożenia , otrzymujemy
(
2
a
d
+
2
b
c
)
2
−
(
a
2
+
d
2
−
b
2
−
c
2
)
2
=
(
2
a
d
+
2
b
c
+
a
2
+
d
2
−
b
2
−
c
2
)
(
2
a
d
+
2
b
c
−
a
2
−
d
2
+
b
2
+
c
2
)
=
(
(
a
+
d
)
2
−
(
b
−
c
)
2
)
(
(
b
+
c
)
2
−
(
a
−
d
)
2
)
=
(
−
a
+
b
+
c
+
d
)
(
a
−
b
+
c
+
d
)
(
a
+
b
−
c
+
d
)
(
a
+
b
+
c
−
d
)
.
{\displaystyle {\begin{aligned}(2ad+2bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}&=(2ad+2bc+a^{2}+d^{2}-b^{2}-c^{2})(2ad+2bc-a^{2}-d^{2}+b^{2}+c^{2})\\&=((a+d)^{2}-(b-c)^{2})((b+c)^{2}-(a-d)^{2})\\&=(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d).\end{aligned}}}
Wprowadzając połowę obwodu
s
{\displaystyle s}
s
=
a
+
b
+
c
+
d
2
,
{\displaystyle s={\frac {a+b+c+d}{2}},}
otrzymujemy równość
16
S
2
=
16
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
16
a
b
c
d
cos
2
α
+
γ
2
{\displaystyle 16S^{2}=16(s-a)(s-b)(s-c)(s-d)-16abcd\cos ^{2}{\frac {\alpha +\gamma }{2}}}
z której, po podzieleniu przez 16 i obustronnym spierwiastkowaniu otrzymujemy wzór Bretschneidera.
Twierdzenie Bretschneidera to uogólnienie wzoru Brahmagupty , będącego z kolei uogólnieniem wzoru Herona . Jeśli czworokąt dany jest wpisany w koło, to przeciwległe kąty sumują się do kąta półpełnego i wtedy
S
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
a
b
c
d
cos
2
π
2
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
.
{\displaystyle S={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}{\frac {\pi }{2}}}}={\sqrt {(s-a)(s-b)(s-c)(s-d)}}.}
Carl Bretschneider. Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes . „C. A. Archiv der Math.”. 2, s. 225–261, 1842. J.L. Coolidge. A Historically Interesting Formula for the Area of a Quadrilateral. Ernest William Hobson: A treatise on plane geometry . Wyd. IV. Cambridge University Press, 1918. F. Strehlke. Zwei neue Sätze vom ebenen und shparischen Viereck und Umkehrung des Ptolemaischen Lehrsatzes . „Archiv der Math.”. 2, s. 33–326, 1842.