Wyrównanie histogramu

Wyrównanie histogramu – metoda przetwarzania obrazów. Polega na poprawianiu kontrastu analizowanego obrazu z wykorzystaniem jego histogramu.

Omówienie

Metoda ta wpływa na powiększenie globalnego kontrastu obrazów, szczególnie gdy wykorzystywany sygnał opisujący obraz jest reprezentowany przez wartości z niewielkiego zakresu. Poprzez rozciągnięcie tych wartości na szerszy zakres, natężenia mogą być lepiej dystrybuowane na histogramie. Pozwala to zwiększyć kontrast we fragmentach o jego niskim poziomie.

Metoda jest użyteczna w obrazach z wyraźnym podziałem na tło i pierwszy plan, takimi, że barwa obu jest albo jasna albo ciemna. W szczególności, może prowadzić do skuteczniejszego obserwowania struktur kostnych w diagnostyce rentgenowskiej oraz do dokładniejszego prezentowania szczegółów na zdjęciach prześwietlonych lub niedoświetlonych. Kluczowymi walorami metody są jej prostota oraz odwracalność. Jeśli funkcja wyrównania histogramu jest znana, wtedy oryginalny histogram może być odzyskany.

Wadą metody jest fakt, że nie rozróżnia sygnału od szumu, co może spowodować wzrost wartości szumu, przy jednoczesnym zmniejszeniu widoczności właściwego sygnału.

W obrazowaniu, gdzie korelacja przestrzenna jest ważniejsza niż intensywność sygnału (jak np. przy rozdzielaniu fragmentów DNA o określonych długościach), wysokie zaszumienie utrudnia wykrywanie poszukiwanych cech. Wyrównywanie histogramu zwiększa szansę ich detekcji, co umożliwia stosowanie łagodniejszych metod chemicznych, mających na celu fizyczne zwiększenie kontrastu obrazowanych fragmentów DNA.

Wyrównanie histogramu powoduje często powstawanie nierealistycznych efektów w fotografii; mimo to może być bardzo użyteczne dla obrazowania w nauce np. termografii, zdjęciach satelitarnych czy diagnostyce rentgenowskiej, w których użytkownik może używać tzw. fałszywych kolorów (false-color). Metoda może również wywoływać niepowołane efekty (widoczny gradient obrazu, tj. kierunkowa zmiana intensywności kolorów) w zastosowaniu do obrazów o niskiej głębi kolorów. Na przykład jeśli użyjemy metodę do 8-bitowego obrazka wyświetlanego w 8-bitowej palecie odcieni szarości, doprowadzi to do zmniejszenia głębi kolorów. Wyrównanie histogramu będzie najbardziej efektywne w zastosowaniu do obrazów o znacznie większej głębi koloru niż rozmiar palety, np. ciągły sygnał lub 16-bitowe obrazy w odcieniach szarości.

Istnieją dwie strategie implementacji wyrównania histogramu – zmiana pikseli obrazka, lub zmiana palety barw. Operację tą możemy wyrazić jako P(M(I)), gdzie I jest oryginalnym obrazem, M to operacja mapowania, zaś P jest paletą. Jeśli zdefiniujemy nową paletę w funkcji mapowania P’=P(M) i zostawimy obraz I niezmieniony, wtedy wyrównanie histogramu jest implementowane jako zmiana palety. W przeciwnej sytuacji, jeśli paleta P zachowuje swoją wartość, a obraz jest modyfikowany w funkcji mapowania jako I’=I(M), wtedy implementacja opiera się na zmianie obrazu. W wielu przypadkach lepszą metodą jest zmiana palety ponieważ zachowuje oryginalny sygnał obrazu.

Uogólnienia tej metody wykorzystują wiele cząstkowych histogramów dla podkreślenia kontrastu w poszczególnych częściach obrazu, zamiast na jego całości. Przykładem takiej metody jest adaptacyjne ograniczenie kontrastu wyrównaniem histogramu, tzw. CLAHE (Contrast Limiting Adaptive Histogram Equalization).

Wyrównanie histogramu znajduje również zastosowanie w biologicznych sieciach neuronowych w celu maksymalizacji wyjściowej szybkości neuronu jako funkcji statystyki wejścia. Okazało się to praktyczne także przy badaniu efektu „pływającej siatkówki” (fly retina). Wyrównanie histogramu jest szczególnym przypadkiem klasy metod zmiany mapowania histogramami. Metody te mają na celu jakościowe przygotowanie obrazu, aby ułatwić ich analizę.

Projekcja wsteczna

Projekcja wsteczna obrazu histogramowanego jest ponownym zastosowaniem zmodyfikowanego histogramu do oryginalnego obrazu, funkcjonująca jako operacja „look-up table” dla jasności piksela.

Implementacja

Rozpatrzmy dyskretny obraz w odcieniach szarości $\{x\}$ i niech $n_{i}$ będzie liczbą pikseli o poziomie szarości $i.$ Prawdopodobieństwo wystąpienia piksela na poziomie $i$ w tym obrazie wynosi:

$p_{x}(i)=p(x=i)={\frac {n_{i}}{n}},\quad 0\leqslant i<L$

gdzie: $L$ określa całkowitą liczbę odcieni szarości na danym obrazie, $n$ określa całkowitą liczbę pikseli na obrazie, a $p_{x}(i)$ określa wartość histogramu obrazu (znormalizowaną do zakresu $[0,1]$) odpowiadającą pikselowi o wartości i.

Zdefiniujmy dystrybuantę dla $p_{x}$ jako

$cdf_{x}(i)=\sum _{j=0}^{i}p_{x}(j),$

która jest również sumarycznym zbiorem znormalizowanych histogramów obrazu.

Chcemy dokonać transformacji z postaci $y=T(x),$ aby uzyskać nowy obraz $\{y\},$ taki, że jego dystrybuanta będzie podlegać linearyzacji poprzez cały zakres wartości, tzn.

$cdf_{y}(i)=iK$

dla pewnego stałego $K.$ Właściwości dystrybuanty pozwalają nam na takie przekształcenie, zdefiniowane jako:

$y=T(x)=cdf_{x}(x)$

Należy zauważyć, że T zwraca odpowiednie wartości dla poziomów w przedziale [0 1]. Żeby zwróciła wartości przeciwne do ich oryginalnych wartości, należy dokonać prostego przekształcenia:

$y'=y\cdot (\max\{x\}-\min\{x\})+\min\{x\}$

Wyrównanie histogramu zdjęć kolorowych

Powyżej przedstawiono opis wyrównania histogramu dla obrazu w odcieniach szarości. Jednakże wyrównanie histogramu można zastosować również do obrazów kolorowych poprzez wyrównanie histogramów dla poszczególnych składowych kolorów obrazu RGB (czerwonej, zielonej i niebieskiej). Zastosowanie tej metody do kolorów składowych RGB obrazu, może powodować znaczne zmiany w balansie kolorów obrazu, ponieważ oddzielne przetwarzanie składowych spowoduje zmiany w stosunkach wartości poszczególnych kanałów. Jeśli jednak obraz zostanie najpierw przekonwertowany do innej przestrzeni kolorów, jak np. CIELab lub HSV, wtedy wyrównywanie histogramu może odnosić się do luminancji lub przedziału wartości, bez efektu zmiany odcienia i nasycenia obrazu.

Przykłady

Mały obraz

Poniższy podobraz 8x8 został użyty jako JPEG. Przedstawiony 8-bitowy obrazek w odcieniach szarości posiada następujące wartości:

${\begin{bmatrix}52&55&61&66&70&61&64&73\\63&59&55&90&109&85&69&72\\62&59&68&113&144&104&66&73\\63&58&71&122&154&106&70&69\\67&61&68&104&126&88&68&70\\79&65&60&70&77&68&58&75\\85&71&64&59&55&61&65&83\\87&79&69&68&65&76&78&94\end{bmatrix}}$

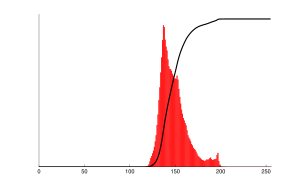
Histogram dla tego obrazu jest pokazany w poniższej tabeli. Wartości pikseli, dla których liczba zliczeń jest równa zero, nie zostały uwzględnione.

Wartość piksela	Liczba zliczeń	Wartość piksela	Liczba zliczeń	Wartość piksela	Liczba zliczeń	Wartość piksela	Liczba zliczeń	Wartość piksela	Liczba zliczeń
52	1	64	2	72	1	85	2	113	1
55	3	65	3	73	2	87	1	122	1
58	2	66	2	75	1	88	1	126	1
59	3	67	1	76	1	90	1	144	1
60	1	68	5	77	1	94	1	154	1
61	4	69	3	78	1	104	2
62	1	70	4	79	2	106	1
63	2	71	2	83	1	109	1

Dystrybuanta rozkładu (cdf) jest przedstawiona poniżej. I tym razem, wartości pikseli, które nie przyczyniają się do wzrostu wartości dystrybuanty (cdf) zostały pominięte.

Wartość piksela	Wartość dystrybuanty	Wartość piksela	Wartość dystrybuanty	Wartość piksela	Wartość dystrybuanty	Wartość piksela	Wartość dystrybuanty	Wartość piksela	Wartość dystrybuanty
52	1	64	19	72	40	85	51	113	60
55	4	65	22	73	42	87	52	122	61
58	6	66	24	75	43	88	53	126	62
59	9	67	25	76	44	90	54	144	63
60	10	68	30	77	45	94	55	154	64
61	14	69	33	78	46	104	57
62	15	70	37	79	48	106	58
63	17	71	39	83	49	109	59

Na podstawie powyższej tabeli, możemy zauważyć, że minimalna wartość dystrybuanty dla tego podobrazu przypada dla piksela o wartości 52, a maksymalna dla piksela o wartości 154. Wartości dystrybuanty wynosząca 64 dla piksela o wartości 154, odpowiada liczbie pikseli na obrazku. Rozkład dystrybuanty musi zostać znormalizowany do przedziału $[0,255].$ Ogólny wzór stosowany do wyrównania histogramu ma następującą postać:

$h(v)=\mathrm {round} \left({\frac {cdf(v)-cdf_{min}}{(M\times N)-cdf_{min}}}\times (L-1)\right)$

Jeśli cdf_min jest minimalną niezerową wartością dystrybuanty (w tym przypadku równą1), M x N daje liczbę pikseli obrazu (dla naszego przykładu wynoszącą 64, gdzie M jest szerokością, a N wysokością) oraz L jest liczbą użytych odcieni szarości (w większości wypadków, tak jak i tutaj, wynosi 256). Wzór na wyrównanie histogramu dla tego szczególnego przypadku ma następującą postać:

$h(v)=\mathrm {round} \left({\frac {cdf(v)-1}{63}}\times 255\right)$

Na przykład wartość dystrybuanty dla piksela o wartości 78 wynosi 46 (piksel o wartości 78 znajduje się w dolnej części 7 kolumny). Znormalizowana wartość dystrybuanty dla tego piksela wynosi teraz:

$h(78)=\mathrm {round} \left({\frac {46-1}{63}}\times 255\right)=\mathrm {round} \left(0{,}714286\times 255\right)=182$

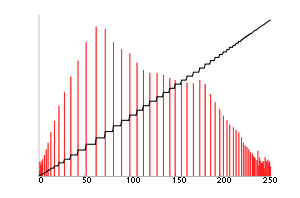
Po skończeniu wyrównania, wartości pikseli wyrównanego obrazu dla znormalizowanego rozkładu dystrybuanty dają następujący wynik:

${\begin{bmatrix}0&12&53&93&146&53&73&166\\65&32&12&215&235&202&130&158\\57&32&117&239&251&227&93&166\\65&20&154&243&255&231&146&130\\97&53&117&227&247&210&117&146\\190&85&36&146&178&117&20&170\\202&154&73&32&12&53&85&194\\206&190&130&117&85&174&182&219\end{bmatrix}}$

Należy zauważyć, że minimalna wartość (52) wynosi teraz 0, a wartość maksymalna (154) wynosi teraz 255.

Obraz oryginalny	Obraz po wyrównaniu histogramu

Pełnowymiarowy obraz

Obraz bez wyrównania histogramu	Histogram (na czerwono) i histogram skumulowany (czarny)
Ten sam obraz po wyrównaniu histogramu	Histogram (na czerwono) i histogram skumulowany (czarny)

Bibliografia

• Tinku Acharya, Ajoy K. Ray, Image Processing: Principles and Applications, Wiley-Interscience 2005, ISBN 0-471-71998-6.
• John C. Russ, The Image Processing Handbook: Fourth Edition, CRC 2002, ISBN 0-8493-2532-3.

Linki zewnętrzne

• „Histogram Equalization” at Generation5
• Page by Ruye Wang with good explanation and pseudo-code. fourier.eng.hmc.edu. [zarchiwizowane z tego adresu (2011-04-14)].