Wzory skróconego mnożenia
Wzory skróconego mnożenia – zestaw tożsamości algebraicznych zawierających potęgi o wykładniku naturalnym oraz dodawanie i odejmowanie; wzory te zawierają wyrażenie algebraiczne takie jak:
- potęgi skończonych sum i różnic:
- różnice dwóch potęg:
- dla wykładników nieparzystych także sumy takich potęg:
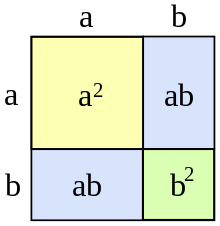
Najprostsze przykłady to te dla wykładnika dwa[1]:
- kwadrat sumy i różnicy:
- różnica kwadratów:
Wzory te zachodzą dla dowolnych liczb rzeczywistych, zespolonych i wszystkich innych pierścieni przemiennych[potrzebny przypis], ponieważ wynikają z podstawowych własności działań jak przemienność, łączność i rozdzielność. Wzory skróconego mnożenia stosuje się w arytmetyce, algebrze i analizie; przykłady ich użycia to[2]:
- przyspieszanie obliczeń, umożliwiające wykonanie pewnych działań arytmetycznych w pamięci;
- działania na pierwiastnikach, np.:
- usuwanie niewymierności z mianowników – przekształcanie odwrotności takich wyrażeń, czyli ich minus pierwszej potęgi;
- pierwiastkowanie ich – przekształcanie ich potęgi ułamkowej;
- przekształcenia równań kwadratowych i funkcji kwadratowych[3][4];
- dowodzenie nierówności[5];
- obliczanie granic ciągów[6].
Wzory te są standardowym elementem wykształcenia matematycznego na poziomie średnim; przykładowo znalazły się one w podstawie programowej polskich liceów i techników, także w zakresie podstawowym[7].
Wykładnik dwa – wzory z kwadratami[edytuj | edytuj kod]
Kwadraty sum i różnic[edytuj | edytuj kod]

Dla dowolnych liczb rzeczywistych zachodzi[8][1]:
Przykłady zastosowań arytmetycznych – obliczanie[2][9]:
- kwadratów liczb naturalnych:
Wzory te mają również wersje dla większej liczby składników, np. dla trzech[5]:
Wzór ten można stosować dla kwadratu dowolnej liczby składników. Po prawej stronie wzoru wystąpią wtedy kwadraty każdego ze składników w nawiasie oraz podwojone iloczyny każdej pary tych składników[potrzebny przypis]:
Różnice można przedstawić w postaci sumy składników o przeciwnym znaku, np.
Wzory te mają także uogólnienie w przestrzeniach unitarnych, zwane tożsamością polaryzacyjną.
Różnice kwadratów[edytuj | edytuj kod]

Różnica kwadratów dwóch liczb to iloczyn sumy tych liczb i ich różnicy[1][8]:
Przykład zastosowania arytmetycznego – usuwanie niewymierności z mianownika[2]:
Sumy kwadratów[edytuj | edytuj kod]
Analogiczna suma nie rozkłada się na wyrażenia rzeczywiste, jednak można rozłożyć ją na iloczyn liczb zespolonych[potrzebny przypis]:
- gdzie to jednostka urojona.
Wykładnik trzy – wzory z sześcianami[edytuj | edytuj kod]

Sześcian sumy i różnicy[8][1]:
Suma i różnica sześcianów[8][1]:
Przykład zastosowania arytmetycznego – usuwanie niewymierności z mianownika[10]:
Wyższe wykładniki[edytuj | edytuj kod]
Różnica czwartych potęg[11]:
Tożsamość Sophie Germain[potrzebny przypis]:
Suma piątych potęg:
Różnica piątych potęg:
Wzory ogólne[edytuj | edytuj kod]
Potęgi sum i różnic[edytuj | edytuj kod]
Potęga naturalna sumy dwóch składników to szczególny przypadek dwumianu Newtona[11]:
Potęga naturalna sumy dowolnej skończonej liczby składników to[potrzebny przypis]:
gdzie
Sumy i różnice potęg[edytuj | edytuj kod]
Różnica dwóch potęg tego samego stopnia naturalnego to[11]:
Oprócz tego[potrzebny przypis]:
Przypisy[edytuj | edytuj kod]
- ↑ a b c d e skróconego mnożenia wzory, [w:] Encyklopedia PWN [dostęp 2023-12-07].
- ↑ a b c
 Paweł Kwiatkowski i Witold Sadowski, Wzory skróconego mnożenia. Przeczytaj, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2023-12-07].
Paweł Kwiatkowski i Witold Sadowski, Wzory skróconego mnożenia. Przeczytaj, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2023-12-07].
- ↑
 Szymon Charzyński, Rozpoznawanie kwadratu dwumianu w trójmianie kwadratowym, kanał Khan Academy na YouTube, 26 kwietnia 2016 [dostęp 2023-12-08].
Szymon Charzyński, Rozpoznawanie kwadratu dwumianu w trójmianie kwadratowym, kanał Khan Academy na YouTube, 26 kwietnia 2016 [dostęp 2023-12-08].
- ↑
 Zależności między wartościami współczynników występujących we wzorach funkcji kwadratowej zapisanej w postaci ogólnej i w postaci kanonicznej, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2023-12-09].
Zależności między wartościami współczynników występujących we wzorach funkcji kwadratowej zapisanej w postaci ogólnej i w postaci kanonicznej, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2023-12-09].
- ↑ a b
 Justyna Cybulska, Wzory skróconego mnożenia na deser. Przeczytaj, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2023-12-08].
Justyna Cybulska, Wzory skróconego mnożenia na deser. Przeczytaj, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2023-12-08].
- ↑ Krysicki i Włodarski 1994 ↓, s. 32.
- ↑
 Podstawa programowa kształcenia ogólnego z komentarzem. Szkoła ponadpodstawowa: liceum ogólnokształcące, technikum oraz branżowa szkoła I i II stopnia, matematyka, Centralna Komisja Egzaminacyjna, cke.gov.pl, s. 15 [dostęp 2023-12-08].
Podstawa programowa kształcenia ogólnego z komentarzem. Szkoła ponadpodstawowa: liceum ogólnokształcące, technikum oraz branżowa szkoła I i II stopnia, matematyka, Centralna Komisja Egzaminacyjna, cke.gov.pl, s. 15 [dostęp 2023-12-08].
- ↑ a b c d Wybrane wzory matematyczne, Warszawa: Centralna Komisja Egzaminacyjna, 2015, s. 3, ISBN 978-83-940902-1-0.
- ↑
 Justyna Cybulska, Wzory skróconego mnożenia na deser. Zadania, zadania generatorowe, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2023-12-08].
Justyna Cybulska, Wzory skróconego mnożenia na deser. Zadania, zadania generatorowe, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2023-12-08].
- ↑ Nowa Era 2020 ↓, s. 67.
- ↑ a b c
 Wzory skróconego mnożenia, Wrocławski Portal Matematyczny, matematyka.wroc.pl, 14 września 2018 [dostęp 2023-12-08].
Wzory skróconego mnożenia, Wrocławski Portal Matematyczny, matematyka.wroc.pl, 14 września 2018 [dostęp 2023-12-08].
Bibliografia[edytuj | edytuj kod]
- Wojciech Babiański, Lech Chańko, Joanna Czarnowska, Grzegorz Janocha, Dorota Ponczek, Jolanta Wesołowska: Matematyka 2. Podręcznik dla liceum ogólnokształcącego i technikum. Wydawnictwo Nowa Era, 2020. ISBN 978-83-267-3900-2.
- Włodzimierz Krysicki, Lech Włodarski: Analiza matematyczna w zadaniach. Wyd. XXI. T. 1. Warszawa: Wydawnictwo Naukowe PWN, 1994. ISBN 83-01-01460-1.























![{\displaystyle {\begin{aligned}{\frac {1}{{\sqrt[{3}]{9}}-2}}&={\frac {{\sqrt[{3}]{9}}^{2}+2{\sqrt[{3}]{9}}+2^{2}}{({\sqrt[{3}]{9}}-2)({\sqrt[{3}]{9}}^{2}+2{\sqrt[{3}]{9}}+2^{2})}}=\\&={\frac {{\sqrt[{3}]{3^{4}}}+2{\sqrt[{3}]{9}}+4}{9-2^{3}}}=\\&=4+3{\sqrt[{3}]{3}}+2{\sqrt[{3}]{9}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96decfa83f12932a2dabdb9b7387b6731b583fac)









