Funkcja o wahaniu ograniczonym

Przykłady funkcji o wahaniu nieograniczonym

Przykłady funkcji o wahaniu ograniczonym

Funkcja o wahaniu ograniczonym – w analizie matematycznej jest to funkcja, której zmienność jest, nieformalnie mówiąc, skończona, czyli funkcja nie oscyluje bez ograniczenia.

Przestrzeń wszystkich funkcji określonych na obszarze $\Omega$ o wahaniu ograniczonym jest oznaczana przez $BV(\Omega ).$

Pojęcie pochodzi od Camille’a Jordana.

Funkcje zmiennej rzeczywistej

Definicja

Całkowite wahanie dla funkcji rzeczywistej $f\colon [a,b]\to \mathbb {R}$ definiujemy jako odpowiednie supremum:

$\sup _{P}\sum _{i}|f(x_{i+1})-f(x_{i})|,$

które jest brane po wszystkich możliwych rozbiciach $P=\{x_{1},\dotsc ,x_{n}\mid x_{1}<\dotsb <x_{n}\}$ przedziału $[a,b].$ Jeśli wahanie funkcji $f$ jest skończone, to powiemy, że jest to funkcja o wahaniu ograniczonym. W przeciwnym wypadku $f$ nazwiemy funkcją o wahaniu nieograniczonym.

Przykład

Przykład funkcji o wahaniu nieograniczonym

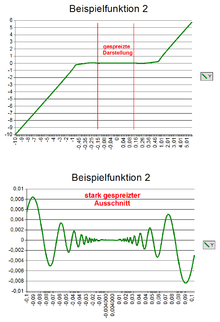
Prostym przykładem funkcji o wahaniu nieograniczonym jest funkcja $f:[0,1]\to \mathbb {R}$ dana wzorem $f(x)=\sin \left({\frac {1}{x}}\right)$ dla $x\neq 0$ oraz $f(0)=0$ (jej wykresem jest sinusoida zagęszczona). Przy $x$ malejącym do zera iloraz ${\tfrac {1}{x}}$ rośnie coraz szybciej w kierunku nieskończoności, więc sinus dla tego argumentu przejdzie przez nieskończoną liczbę oscylacji, co oznacza nieskończoną liczbę przejść od $-1$ do $1$ i z powrotem do $-1.$ Pokazuje to obrazek po prawej stronie.

To, że przykładowa funkcja $f$ ma wahanie nieograniczone, uzasadnia się wprost z definicji, wystarczy bowiem wziąć ciąg rozbić $P_{n}=\left\{{\frac {2}{(2n+1)\pi }},\dots ,{\frac {2}{3\pi }},{\frac {2}{\pi }}\right\}$ i wtedy kolejne sumy

$\sum _{i=2}^{n}\left|f\left({\frac {2}{(2i+1)\pi }}\right)-f\left({\frac {2}{(2i-1)\pi }}\right)\right|$

są równe $2n,$ co też, z racji możliwości wzięcia dowolnie dużego $n,$ daje nieograniczoność wahania funkcji $f.$

Powyższa definicja może być również łatwo rozszerzona do opisu wahania funkcji zespolonych o argumentach rzeczywistych.

Funkcje wielu zmiennych

W przypadku funkcji wielu zmiennych, funkcjami o wahaniu ograniczonym nazywamy te funkcje, których pochodnymi w sensie dystrybucyjnymi są skończone miary Radona o wartościach wektorowych.

Definicja

Niech $\Omega$ będzie otwartym podzbiorem $\mathbb {R} ^{n}.$ Funkcję $u\in L^{1}(\Omega )$ nazwiemy funkcją o wahaniu ograniczonym, jeśli jej pochodna w sensie dystrybucji jest skończoną wektorową miarą Radona, czyli istnieje $Du\in {\mathcal {M}}(\Omega ,\mathbb {R} ^{n})$ takie, że

$\int _{\Omega }u(x)\,\operatorname {div} {\varphi }(x)\mathrm {d} x=-\int _{\Omega }\langle \varphi ,Du(x)\rangle \qquad {\text{dla wszystkich }}{\varphi }\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n}).$

Związek z krzywymi prostowalnymi

Funkcja ciągła $f\colon [a,b]\to \mathbb {R}$ może być rozumiana jako droga w przestrzeni metrycznej $\mathbb {R} .$ Wówczas $f$ jest funkcją o wahaniu ograniczonym wtedy i tylko wtedy, gdy $f$ jest krzywą prostowalną, czyli ma skończoną długość.

Związek z teorią miary

W teorii miary, funkcje o wartościach rzeczywistych lub zespolonych o wahaniu ograniczonym są w istocie dystrybuantami miar borelowskich odpowiednio ze znakiem lub zespolonych, to jest funkcjami danymi wzorem:

$F_{\mu }(x)=\mu \left((-\infty ,x]\right)$

dla ustalonej miary $\mu$.

Bibliografia

• Jürgen Elstrodt: Maß- und Integrationstheorie. Wyd. 5. Berlin: Springer, 2007. ISBN 978-3-540-49977-0.brak strony w książce
• Gerald Teschl: Topics in Real and Functional Analysis. 2011.brak strony w książce
• Luigi Ambrosio, Nicola Fusco, Diego Pallara: Functions of Bounded Variation and Free Discontinuity Problems. Oxford: 2000.brak strony w książce