Równanie pędu Cauchy’ego
Wprowadzenie[edytuj | edytuj kod]
Równanie pędu Cauchy’ego – wektorowe równanie różniczkowe cząstkowe zaproponowane przez Cauchy’ego, które opisuje nierelatywistyczny transport pędu w każdym ośrodku ciągłym[1]. Dane jest ono następująco:
gdzie:
- – gęstość,
- – pochodna substancjalna prędkości,
- – operator nabla,
- – tensor naprężenia,
- – przyspieszenie związane z siłami masowymi.
Jest to równanie wektorowe (tzn. jego rozwiązaniem jest pole wektorowe) które po rozwinięciu w układzie kartezjańskim ma postać trzech równań – po jednym dla każdej składowej wynikowego pola wektorowego[2]:
Jak widać układ nie jest zamknięty, gdyż mamy tylko 3 równania a 13 niewiadomych tj. (skalar – 1 niewiadoma), (vektor – 3 niewiadome), (macierz – 9 niewiadomych). Poza tym są wiadome w ramach warunków początkowych/brzegowych.
Detale dotyczące Dla operacja „” pomiędzy operatorem nabla a tensorem naprężenia NIE JEST mnożeniem macierzy – nie można użyć lewostronnego mnożenia pomiędzy wektorem kontrawariantnym (kolumnowym; „pionowym”; co wynika z definicji operatora) a macierzą. Wyrażenie ma tylko symboliczne znaczenie. Standardowo dywergencja jest zdefiniowana jako operator na polu wektorowym (jako Iloczyn skalarny pomiędzy operatorem nabla i wektorem (więcej: Pochodna kowariantna)), ale może zostać rozszerzona na pola tensorowe 2 rzędu (macierze), jednak w tym przypadku mamy do czynienia z inną operacją: . W ogólności mamy W kartezjańskim układzie współrzędnych możemy tę operację zapisać jako mnożenie macierzy (poniżej używamy „pusty” symbol mnożenia) w następujący sposób:
gdzie rezultat (po prawej) jest kolumnowym wektorem, oznacza transpozycję. Transpozycja operatora nabla w powyższych równaniach pozwala na użycie lewostronnego mnożenia macierzy (od drugiej równości), kolejna transpozycja (wykonana po mnożeniu macierzowym) zmienia rezultat z wektora wierszowego na kolumnowy (kontrawariantnym) co powzowli na dodawanie pozostałych składowych równania pędu (które są wektorami kolumnowymi) jak np. Dla przypadku gdy sigma jest tensorem symetrycznym (np. dla płynu Newtonowskiego w równaniach Naviera-Stokesa bazujących na równaniu pędu Cauchego) zachodzi Jednak w ogólności nie powinniśmy mylić operacji z operacją która dla niesymetrycznego tensora sigma (używanym np. dla modelowania płynów nienewtonowskich jak polimery) daje inne rezultaty[3]
Wyprowadzenie różniczkowe[edytuj | edytuj kod]
Wychodzimy od uogólnionej zasady zachowania pędu, którą można zapisać następująco: „zmiana pędu układu jest proporcjonalna do siły wypadkowej działającej na ten układ” wyraża się ona wzorem:
gdzie:
- – pęd w chwili
- – uśredniona w czasie siła.
Po podzieleniu przez i przejściu do granicy otrzymujemy:
Skupimy się teraz kolejno na wyznaczeniu lewej, a następnie prawej strony powyższego równania dla stałej masy w różniczkowej sześciennej objętości kontrolnej (czyli elemencie ciała) której pęd i działające nań siły chcemy zbadać. Na koniec zestawimy lewą i prawą stronę powyższego równania, otrzymując równanie Pędu Cauchy’ego.
Zacznijmy od prawej strony równania[edytuj | edytuj kod]
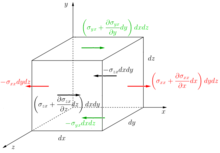

Siły dzielimy na masowe i powierzchniowe
Na ścianki objętości kontrolnej działają siły powierzchniowe. Składowa X tych sił (w formie iloczynu naprężenia i pola powierzchni np. ), dla każdej ścianki, została umieszczona na rysunku z elementem sześciennym.
Wyjaśnienie wartości sił (przybliżeń i znaków minus) na ściankach sześcianu Wyjaśnienia wymaga dlaczego przy naprężeniach na ściankach leżących na osiach współrzędnych mamy znak minus (np. na lewej ściance mamy wartość ). Dla uproszczenia skupmy się na lewej ściance z naprężeniem Znak minus spowodowany jest tym, że wektor normalny do tej ścianki jest ujemnym wektorem jednostkowym. Wówczas przy obliczaniu wektora naprężenia z definicji zatem składowa x tego wektora to (podobne rozumowanie używamy dla naprężeń na ściance dolnej i tylnej tj.: ).
Drugim elementem wymagającym wyjaśnienia jest przybliżenie wartości naprężeń na ściankach przeciwległych do ścianek leżących na osiach. Skupmy się na ściance prawej na której naprężenie jest przybliżeniem naprężenia ze ścianki lewej w punktach o wsp. i wynosi ono To przybliżenie wzięło się z zastosowania wzoru Taylora na przybliżenie funkcji tj.:
Ponieważ wartość jest nieskończenie mniejsza od wartości więc wszystkie wyrazy z w potęgach wyższych niż jeden możemy porzucić, uznając za nieistotne (argument Leibnitza - związany z iloczynem pochodnych) . W ten sposób otrzymaliśmy szukane przybliżenie naprężenia na przeciwległej ściance. Bardziej intuicyjne przedstawienie przybliżenia wartości w punkcie obrazuje rysunek pod sześcianem. Podobne rozumowanie przeprowadzamy dla przybliżeń naprężeń
Sumując siły (ich składowe X) działające na każdą ze ścian, otrzymujemy:
Po uporządkowaniu oraz po wykonaniu podobnego rozumowania dla składowych (nie ma ich na rysunku – będą to wektory równoległe odpowiednio do osi Y i Z) otrzymamy:
W zapisie operatorowym możemy to wówczas zapisać:
Na wnętrze objętości kontrolnej działają siły masowe, które zapiszemy z wykorzystaniem pola przyspieszenia (którym może być np. przyspieszenie ziemskie ):
Lewa strona równania[edytuj | edytuj kod]
Wyznaczmy pęd:
Ponieważ założyliśmy, że badana masa jest stała więc
Porównanie lewej i prawej strony równania[edytuj | edytuj kod]
Otrzymamy:
Dzieląc przez dostaniemy:
co kończy wywód.
Przypisy[edytuj | edytuj kod]
- ↑ D.J. Acheson: Elementary Fluid Dynamics. Oxford University Press, 1990, s. 205. ISBN 0-19-859679-0.
- ↑ W.Z. Berdahl: Behavior of a Vorticity-Influenced Asymmetric Stress Tensor in Fluid Flow. AIR FORCE WRIGHT AERONAUTICAL LABORATORIES, 1986, s. 13 (poniżej głównego równania, autor opisuje: ).
- ↑ Piaras Kelly: Solid Mechanics Part III. University of Auckland, 2019, s. 119.


![{\displaystyle \rho \;\mathrm {[kg/m^{3}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d89fceac79b401e42d3f4fd924b679c51fb9d36)
![{\displaystyle d{\vec {v}}/dt=\partial _{t}{\vec {v}}+{\vec {v}}\cdot \nabla {\vec {v}}\;\mathrm {[m/s^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/08305c24d52903c0ca7aac6b6500953335a511b6)
![{\displaystyle \nabla \;\mathrm {[1/m]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca3da8d68e7e6abd955f5f31db852e3492b5fb3)
![{\displaystyle {\boldsymbol {\sigma }}\;\mathrm {[Pa=N/m^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/01b33af2ef9334bd5ebff0dc4be1aa6befc515fb)
![{\displaystyle {\vec {f}}\;\mathrm {[m/s^{2}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/92867e6e8438f94e7b4f69ce879b603badd25bec)
![{\displaystyle {\begin{aligned}x&:&\rho \left({\frac {\partial u}{\partial t}}+u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}+w{\frac {\partial u}{\partial z}}\right)&={\frac {\partial \sigma _{xx}}{\partial x}}+{\frac {\partial \sigma _{yx}}{\partial y}}+{\frac {\partial \sigma _{zx}}{\partial z}}+\rho f_{x}\\[8pt]y&:&\rho \left({\frac {\partial v}{\partial t}}+u{\frac {\partial v}{\partial x}}+v{\frac {\partial v}{\partial y}}+w{\frac {\partial v}{\partial z}}\right)&={\frac {\partial \sigma _{xy}}{\partial x}}+{\frac {\partial \sigma _{yy}}{\partial y}}+{\frac {\partial \sigma _{zy}}{\partial z}}+\rho f_{y}\\[8pt]z&:&\rho \left({\frac {\partial w}{\partial t}}+u{\frac {\partial w}{\partial x}}+v{\frac {\partial w}{\partial y}}+w{\frac {\partial w}{\partial z}}\right)&={\frac {\partial \sigma _{xz}}{\partial x}}+{\frac {\partial \sigma _{yz}}{\partial y}}+{\frac {\partial \sigma _{zz}}{\partial z}}+\rho f_{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d91f48ecb42ece62a3c114de26f5f671c520c59f)









![{\displaystyle \nabla \cdot {\boldsymbol {\sigma }}=(\nabla ^{T}{\boldsymbol {\sigma }})^{T}=\left({\begin{bmatrix}{\frac {\partial }{\partial x}}\\{\frac {\partial }{\partial y}}\\{\frac {\partial }{\partial z}}\end{bmatrix}}^{T}{\begin{bmatrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{bmatrix}}\right)^{T}=\left(\left[{\tfrac {\partial }{\partial x}}\ \ {\tfrac {\partial }{\partial y}}\ \ {\tfrac {\partial }{\partial z}}\right]{\begin{bmatrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{bmatrix}}\right)^{T}={\begin{bmatrix}{\frac {\partial \sigma _{xx}}{\partial x}}+{\frac {\partial \sigma _{yx}}{\partial y}}+{\frac {\partial \sigma _{zx}}{\partial z}}\\{\frac {\partial \sigma _{xy}}{\partial x}}+{\frac {\partial \sigma _{yy}}{\partial y}}+{\frac {\partial \sigma _{zy}}{\partial z}}\\{\frac {\partial \sigma _{xz}}{\partial x}}+{\frac {\partial \sigma _{yz}}{\partial y}}+{\frac {\partial \sigma _{zz}}{\partial z}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5950ae3db1c22cf98dad9afe211bcdcc33236e63)

















![{\displaystyle -\sigma _{xx}dydz\ \mathrm {[Pa\cdot m\cdot m={\frac {N}{m^{2}}}\cdot m\cdot m=N]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f46f978e902e6c1f8f6fa33e5cf2287d4577d31)


![{\displaystyle {\vec {n}}=[-1,0,0]=-{\vec {e}}_{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4189d48c7082b664259d96d22891535ffb43b113)
![{\displaystyle {\vec {s}}={\vec {n}}\cdot {\boldsymbol {\sigma }}=[-\sigma _{xx},-\sigma _{xy},-\sigma _{xy}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baead09cbdfdc8bc341800e70e6220ae0fd82319)























