Twierdzenie Blaschkego-Lebesgue’a

Z Wikipedii, wolnej encyklopedii
Trójkąt Reuleaux

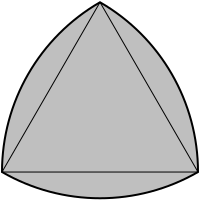
Twierdzenie Blaschkego-Lebesgue’a – twierdzenie z dziedziny geometrii euklidesowej udowodnione przez Wilhelma Blaschkego i Henriego Lebesgue’a.

Twierdzenie[edytuj | edytuj kod]

Trójkąt Reuleaux jest figurą o najmniejszej powierzchni ze wszystkich figur o zadanej stałej szerokości[1].


Zobacz też[edytuj | edytuj kod]

Przypisy[edytuj | edytuj kod]

  1. ↑ Evans M. Harrell. A direct proof of a theorem of Blaschke and Lebesgue. „The Journal of Geometric Analysis”, Marzec 2002. Springer. 
Źródło: „https://pl.wikipedia.org/w/index.php?title=Twierdzenie_Blaschkego-Lebesgue’a&oldid=56968217”