Uogólniona funkcja logistyczna
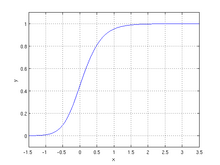




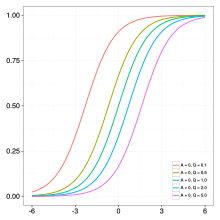
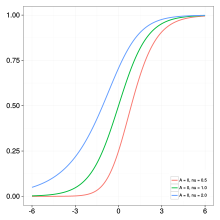
Uogólniona funkcja (lub krzywa) logistyczna – funkcja generująca krzywe w kształcie litery S. Jest rozszerzeniem funkcji logistycznej. Została opracowana jako model wzrostu populacji i rozprzestrzeniania się zjawisk przez biologa F. J. Richardsa w 1959, stąd czasem nazywana jest krzywą Richardsa[1][2].
Definicja
[edytuj | edytuj kod]Uogólniona funkcja logistyczna ma następującą postać[3]:
Gdzie to wybrana miara badanego zjawiska, zaś to czas. Krzywa ma sześć parametrów:
- – lewa asymptota pozioma;
- – prawa asymptota pozioma, jeżeli ; jeśli i , nazywa się pojemnością środowiska;
- – tempo wzrostu;
- – parametr wpływający na to, w pobliżu której asymptoty występuje maksymalny wzrost.
- – parametr powiązany z wartością
- – parametr zazwyczaj przyjmujący wartość 1. W przeciwnym razie prawa asymptota to
Równanie może również być zapisane w formie:
gdzie może być traktowane jako moment początkowy, w którym .
Wreszcie, zapis zawierający zarówno parametr , jak i może okazać się wygodny:
Takie sformułowanie ułatwia ustawienie zarówno czasu początkowego, jak i wartości w tym czasie.
Jeżeli , otrzymamy funkcję logistyczną z punktem przegięcia w czasie .
Równanie różniczkowe
[edytuj | edytuj kod]Szczególnym przypadkiem uogólnionej funkcji logistycznej jest:
- ,
co jest rozwiązaniem równania różniczkowego Richardsa (RDE):
z warunkiem początkowym
gdzie
pod warunkiem że i
Klasyczne logistyczne równanie różniczkowe jest szczególnym przypadkiem powyższego równania, gdzie = 1, natomiast krzywą Gompertza można odzyskać w granicy pod warunkiem że:
W rzeczywistości dla małego
Równanie różniczkowe Richardsa umożliwia modelowanie wielu zjawisk wzrostu, pojawiających się w takich dziedzinach, jak onkologia i epidemiologia.
Gradient uogólnionej funkcji logistycznej
[edytuj | edytuj kod]Przy estymacji parametrów na podstawie danych często konieczne jest obliczenie pochodnych cząstkowych funkcji logistycznej względem parametrów w danym punkcie danych (patrz[4]). Jeżeli , mamy:
Specjalne przypadki
[edytuj | edytuj kod]Następujące funkcje są konkretnymi przypadkami krzywych Richardsa:
Przypisy
[edytuj | edytuj kod]- ↑ F.J. Richards, A Flexible Growth Function for Empirical Use, „Journal of Experimental Botany”, 10 (2), 1959, s. 290–301, DOI: 10.1093/jxb/10.2.290, ISSN 0022-0957 [dostęp 2024-06-21] (ang.).
- ↑ Marco Mingione i inni, Spatio-temporal modelling of COVID-19 incident cases using Richards’ curve: An application to the Italian regions, „Spatial Statistics”, 49, Spatio-temporal spread of Covid patterns: its spread, causes and scale, 2022, s. 100544, DOI: 10.1016/j.spasta.2021.100544, ISSN 2211-6753, PMID: 36407655, PMCID: PMC9643104 [dostęp 2024-06-21].
- ↑ Piotr Dyga, Przetwarzanie informacji obrazowej [online], 2022.
- ↑ Desta Fekedulegn, Mairitin P. Mac Siurtain. Parameter Estimation of Nonlinear Growth Models in Forestry. „Silva Fennica”. 33 (4), s. 327–336, 1999. DOI: 10.14214/sf.653. [zarchiwizowane z adresu].
Bibliografia
[edytuj | edytuj kod]- F. J. Richards. A Flexible Growth Function for Empirical Use. „Journal of Experimental Botany”. 10 (2), s. 290–300, 1959. DOI: 10.1093/jxb/10.2.290.
- J. S. Pella. A Generalised Stock-Production Model. „Bull. Inter-Am. Trop. Tuna Comm”. 13, s. 421–496, 1969.
- Y. C. Lei. Features and Partial Derivatives of Bertalanffy–Richards Growth Model in Forestry. „Nonlinear Analysis: Modelling and Control”. 9 (1), s. 65–73, 2004. DOI: 10.15388/NA.2004.9.1.15171.




























