Filtr o nieskończonej odpowiedzi impulsowej: Różnice pomiędzy wersjami
| [wersja przejrzana] | [wersja przejrzana] |
drobne redakcyjne |
m drobne techniczne, drobne redakcyjne |
||
| Linia 1: | Linia 1: | ||
'''Filtr o nieskończonej odpowiedzi impulsowej''' ({{ang.| |
'''Filtr o nieskończonej odpowiedzi impulsowej''' ('''IIR''' filter {{ang.|Infinite Impulse Response}}) – rodzaj [[filtr cyfrowy|filtru cyfrowego]], który w odróżnieniu od filtrów [[Filtr o skończonej odpowiedzi impulsowej|FIR]] jest układem rekursywnym. IIR oznacza nieskończoną odpowiedź impulsową (w polskiej literaturze stosowany jest również skrót NOI). Znaczy to tyle, że reakcja na pobudzenie o skończonym czasie trwania jest teoretycznie nieskończenie długa. Jest to efektem występowania pętli sprzężenia zwrotnego widocznej na schemacie blokowym (porównaj ze schematem filtru FIR). |
||
| ⚫ | |||
| ⚫ | |||
Na powyższym schemacie moduły <math>z^{-1}</math> oznaczają opóźnienie sygnału o jedną próbkę, natomiast <math>a_{i}</math> oraz <math>b_{i}</math> są współczynnikami filtru. |
Na powyższym schemacie moduły <math>z^{-1}</math> oznaczają opóźnienie sygnału o jedną próbkę, natomiast <math>a_{i}</math> oraz <math>b_{i}</math> są współczynnikami filtru. |
||
| Linia 7: | Linia 6: | ||
[[transmitancja operatorowa|Transmitancję]] filtru IIR można opisać: |
[[transmitancja operatorowa|Transmitancję]] filtru IIR można opisać: |
||
: <math>H(z) = \frac{Y(z)} {X(z)}</math> |
: <math>H(z) = \frac{Y(z)} {X(z)}</math> |
||
gdzie: |
|||
| ⚫ | |||
: <math>Y(z)</math> – transformata Z wyjścia, |
|||
| ⚫ | |||
lub po rozpisaniu wzorów na wielomiany opisujące bieguny i zera: |
lub po rozpisaniu wzorów na wielomiany opisujące bieguny i zera: |
||
: <math>H(z) = \frac{a_{0}+a_{1}z^{-1}+...+a_{p}z^{-p}} {1-(b_{0}z^{-1}+...+b_{q}z^{-q})}</math> |
: <math>H(z) = \frac{a_{0}+a_{1}z^{-1}+...+a_{p}z^{-p}} {1-(b_{0}z^{-1}+...+b_{q}z^{-q})}</math> |
||
| Linia 30: | Linia 30: | ||
Rozważmy działanie filtru o nieskończonej odpowiedzi impulsowej na prostym przykładzie. Załóżmy, że chcemy estymować średni koszt użytkowania energii elektrycznej na podstawie rachunku za prąd z bieżącego miesiąca <math>x(n)</math> oraz oszacowanej wartości z poprzedniego miesiąca <math>y(n-1)</math>: |
Rozważmy działanie filtru o nieskończonej odpowiedzi impulsowej na prostym przykładzie. Załóżmy, że chcemy estymować średni koszt użytkowania energii elektrycznej na podstawie rachunku za prąd z bieżącego miesiąca <math>x(n)</math> oraz oszacowanej wartości z poprzedniego miesiąca <math>y(n-1)</math>: |
||
<math>y(n) = \frac{y(n-1) + x(n)}{2} = 0{,}5\cdot y(n-1) + 0{,}5 \cdot x(n) </math> |
: <math>y(n) = \frac{y(n-1) + x(n)}{2} = 0{,}5\cdot y(n-1) + 0{,}5 \cdot x(n) </math> |
||
gdzie: |
|||
: <math>n</math> – numer miesiąca, |
|||
: <math>x(n)</math> – wartość rachunku za bieżący miesiąc, |
|||
: <math>y(n)</math> – oszacowana wartość w bieżącym miesiącu, |
|||
: <math>y(n-1)</math> – oszacowanie wartości średniej w poprzednim miesiącu. |
|||
Dla <math>n=1</math>, pojawia się problem brzegowy, ponieważ nie dysponujemy oszacowaniem <math>y(0)</math> - przyjmiemy, że <math>y(0)=0</math>. Przykładowo: |
Dla <math>n=1</math>, pojawia się problem brzegowy, ponieważ nie dysponujemy oszacowaniem <math>y(0)</math> - przyjmiemy, że <math>y(0)=0</math>. Przykładowo: |
||
| ⚫ | |||
<math>y( |
: <math>y(2) = 0{,}5\cdot x(2) + 0{,}5 \cdot y(1) = 0{,}5 \cdot 12 + 0{,}5 \cdot 27 = 19{,}5</math> |
||
| ⚫ | |||
Wartości kolejnych próbek wejściowych <math>x(n)</math> (rachunków) oraz szacowanych wartości średnich <math>y(n)</math> przedstawiono w tabeli: |
Wartości kolejnych próbek wejściowych <math>x(n)</math> (rachunków) oraz szacowanych wartości średnich <math>y(n)</math> przedstawiono w tabeli: |
||
{| class="wikitable" |
:{| class="wikitable" style="text-align:center" |
||
! width="80px" | <math>n</math> |
|||
! width="30px" | 1 |
|||
! width="30px" | 2 |
|||
! width="30px" | 3 |
|||
! width="30px" | 4 |
|||
! width="30px" | 5 |
|||
! width="30px" | 6 |
|||
! width="30px" | 7 |
|||
! width="30px" | 8 |
|||
! width="30px" | 9 |
|||
! width="30px" | 10 |
|||
! width="30px" | 11 |
|||
! width="30px" | 12 |
|||
|- |
|- |
||
! <math>x(n)</math> |
|||
| 24 |
| 24 |
||
| 27 |
| 27 |
||
| Linia 71: | Linia 72: | ||
| 0 |
| 0 |
||
|- |
|- |
||
! <math>y(n)</math> |
|||
| 12 |
| 12 |
||
| 19,5 |
| 19,5 |
||
| Linia 87: | Linia 88: | ||
Wykres próbek wejściowych <math>x(n)</math> oraz wyjściowych <math>y(n)</math> przedstawiono na wykresie poniżej (sygnał określony jest tylko dla dyskretnych wartości <math>n</math>, natomiast linie pomagają zaobserwować trend sygnału): |
Wykres próbek wejściowych <math>x(n)</math> oraz wyjściowych <math>y(n)</math> przedstawiono na wykresie poniżej (sygnał określony jest tylko dla dyskretnych wartości <math>n</math>, natomiast linie pomagają zaobserwować trend sygnału): |
||
| ⚫ | |||
| ⚫ | |||
Podobnie jak poprzednio, na podstawie przykładu można wysnuć następujące wnioski: |
Podobnie jak poprzednio, na podstawie przykładu można wysnuć następujące wnioski: |
||
| Linia 95: | Linia 95: | ||
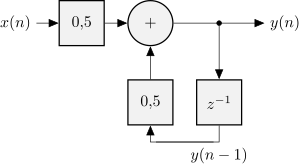
Realizację filtru przestawiono na rysunku poniżej: |
Realizację filtru przestawiono na rysunku poniżej: |
||
| ⚫ | |||
| ⚫ | |||
== Zobacz też == |
== Zobacz też == |
||
Wersja z 08:24, 15 lip 2015
Filtr o nieskończonej odpowiedzi impulsowej (IIR filter ang. Infinite Impulse Response) – rodzaj filtru cyfrowego, który w odróżnieniu od filtrów FIR jest układem rekursywnym. IIR oznacza nieskończoną odpowiedź impulsową (w polskiej literaturze stosowany jest również skrót NOI). Znaczy to tyle, że reakcja na pobudzenie o skończonym czasie trwania jest teoretycznie nieskończenie długa. Jest to efektem występowania pętli sprzężenia zwrotnego widocznej na schemacie blokowym (porównaj ze schematem filtru FIR).
Na powyższym schemacie moduły oznaczają opóźnienie sygnału o jedną próbkę, natomiast oraz są współczynnikami filtru.
Transmitancję filtru IIR można opisać:
gdzie:
- – transformata Z wyjścia,
- – transformata Z wejścia
lub po rozpisaniu wzorów na wielomiany opisujące bieguny i zera:
Zera transmitancji determinowane są przez miejsca zerowe wielomianu licznika, zaś miejsca zerowe wielomianu mianownika określają bieguny transmitancji.
Zalety i wady
Ze względu na dużą elastyczność w kształtowaniu przebiegu funkcji za pomocą ilorazu wielomianów, znacznie łatwiej uzyskać pożądaną charakterystykę używając filtru IIR niskiego rzędu niż filtru FIR. Wynikają z tego dwie podstawowe zalety filtrów IIR w porównaniu do FIR:
- Niska złożoność obliczeniowa
- Niewielkie zapotrzebowanie na pamięć operacyjną.
Te zalety spowodowały duże zainteresowanie filtrami IIR i burzliwy rozwój teorii ich projektowania w latach 70. XX w., które przypadają na początki rozwoju technik CPS, gdy nie były dostępne procesory o odpowiedniej mocy.
Do wad filtrów IIR należy zaliczyć:
- Rekursywność filtru wprowadza potencjalne zagrożenie utraty stabilności (odpowiedź filtru w sposób niekontrolowany narasta do nieskończoności); niestabilność może mieć miejsce wtedy, gdy bieguny transmitancji (miejsca zerowe wielomianu w mianowniku) znajdą się poza okręgiem jednostkowym na płaszczyźnie zespolonej
- Projektowanie filtrów IIR jest znacznie trudniejsze niż w przypadku filtrów FIR (nie tylko ze względu na dodatkowy warunek zapewnienia stabilności)
- Filtry IIR są znacznie bardziej wrażliwe na błędy zaokrągleń: zaokrąglenia wartości współczynników mogą znacząco zmienić charakterystykę, zaokrąglenia wartości sygnału i wyników pośrednich wprowadzają szum, który może się akumulować
- Nie da się ich zaimplementować jako filtrów o liniowej fazie, czyli takich, które wprowadzają takie samo opóźnienie grupowe dla wszystkich składowych częstotliwościowych przepuszczanego sygnału.
Z uwagi na rosnącą wydajność układów cyfrowych i procesorów sygnałowych, filtry IIR nie są obecnie tak chętnie wykorzystywane jak dawniej, a największą popularność mają filtry FIR, które nie mają wyżej wymienionych wad.
Przykład
Rozważmy działanie filtru o nieskończonej odpowiedzi impulsowej na prostym przykładzie. Załóżmy, że chcemy estymować średni koszt użytkowania energii elektrycznej na podstawie rachunku za prąd z bieżącego miesiąca oraz oszacowanej wartości z poprzedniego miesiąca :
gdzie:
- – numer miesiąca,
- – wartość rachunku za bieżący miesiąc,
- – oszacowana wartość w bieżącym miesiącu,
- – oszacowanie wartości średniej w poprzednim miesiącu.
Dla , pojawia się problem brzegowy, ponieważ nie dysponujemy oszacowaniem - przyjmiemy, że . Przykładowo:
Wartości kolejnych próbek wejściowych (rachunków) oraz szacowanych wartości średnich przedstawiono w tabeli:
1 2 3 4 5 6 7 8 9 10 11 12 24 27 31 59 33 37 0 0 0 0 0 0 12 19,5 25,3 42,1 37,6 37,3 18,6 9,3 4,7 2,3 1,2 0,6
Wykres próbek wejściowych oraz wyjściowych przedstawiono na wykresie poniżej (sygnał określony jest tylko dla dyskretnych wartości , natomiast linie pomagają zaobserwować trend sygnału):
Podobnie jak poprzednio, na podstawie przykładu można wysnuć następujące wnioski:
- zaprojektowany filtr wygładza sygnał wejściowy - nagła zmiana sygnału wejściowego dla została stłumiona,
- od chwili sygnał wejściowy zanika. Sygnał wyjściowy dąży do zera, aczkolwiek tej wartości nigdy nie osiągnie. Jest to cecha charakterystyczna filtrów o nieskończonej odpowiedzi impulsowej (NOI).
Realizację filtru przestawiono na rysunku poniżej:
Zobacz też
Bibliografia
- Bartosz Ziółko, M. Ziółko Przetwarzanie mowy, Wydawnictwa AGH, 2012.
- Michał Tadeusiewicz, Signals and Systems, Wydawnictwo Politechniki Łódzkiej, 2004.
- Przemysław Barański, Przekształcenie Z - zastosowania w filtracji cyfrowej sygnałów - zbiór zadań, Wydawnictwo Politechniki Łódzkiej, 2014.