Stała Michaelisa

Stała Michaelisa – współczynnik występujący w modelu Michaelisa-Menten reakcji enzymatycznej. Jest definiowany jako stężenie substratu, przy którym szybkość reakcji enzymatycznej jest równa połowie jej szybkości maksymalnej [1][2][a]. Stała ta jest wyrażana w molach na dm³ i określa powinowactwo enzymu do substratu: im jest mniejsza, tym powinowactwo jest większe, natomiast duża wartość tej stałej mówi o małym powinowactwie enzymu do substratu.
Wartość stałej Km dla większości enzymów przyjmuje wartości z zakresu 10−5 do 10−3 mol/dm3.
Równanie Michaelisa-Menten, pochodzące od nazwisk Leonora Michaelisa i Maud Menten, opisuje zależność szybkości reakcji od stężenia substratu:
Z równania Michaelisa-Menten wynika, że przy stałym stężeniu enzymu szybkość reakcji w pewnych granicach zależy od stężenia substratu. Na wykresie zależności szybkości reakcji od stężenia substratu widoczne jest, że:
- przy niewielkim stężeniu substratu w stosunku do stężenia enzymu pojawia się zależność liniowa między stężeniem substratu a szybkością reakcji; ta sytuacja odpowiada reakcji pierwszego rzędu opisywanej równaniem kinetycznym
- w przypadku dużego stężenia substratu szybkość reakcji zbliża się do jej maksymalnej wartości, a stężenie substratu nie ma wpływu na szybkość reakcji, sytuacja ta odpowiada kinetyce zerowego rzędu opisywanej równaniem Tego typu reakcja ma miejsce w przypadku całkowitego wysycenia enzymu substratem.
Na stałą Michaelisa wpływa:
- pH
- rodzaj substratu
- siła jonowa
- temperatura.
Nie zależy ona natomiast od stężenia enzymu.
Wyprowadzenie równania[edytuj | edytuj kod]
Prawdziwość powyższego równania opiera się na przedstawionym poniżej schemacie reakcji na dwóch kluczowych założeniach: całkowite stężenie enzymu i stężenie produktu pośredniego nie zmieniają się w czasie. Najbardziej odpowiednim równaniem Michaelisa-Menten jest równanie opisane przez Briggsa i J.B.S. Haldane, które przedstawiono poniżej (należy zauważyć, że eksperymentalny parametr również jest używany, ale w tym przypadku jest równy parametrowi kinetycznemu ):
Założono, że reakcja enzymatyczna jest nieodwracalna, a produkt nie kompleksuje się z enzymem.
Pierwszym założeniem w tym wyprowadzeniu jest pseudostan równowagi chemicznej, założenie określające, że stężenie enzymu połączonego z substratem zmienia się wolniej niż stężenie produktu i substratu . Umożliwia to ustalenie stopnia zmian jako zero, a także zapisanie stopnia tworzenia produktu jako:
Drugim kluczowym założeniem jest to, że całkowite stężenie enzymu nie zmienia się w czasie, zatem całkowite stężenie enzymu można zapisać jako sumę wolnego enzymu w roztworze i tego, który jest już związany z substratem
Podstawiając to do równania (2), otrzymuje się wyrażenie na [ES], które w rezultacie może być wykorzystane w równaniu (3), aby znaleźć równanie na stopień tworzenia produktu:
Ponieważ stężenie substratu w trakcie przebiegu reakcji ulega zmianie, początkowa szybkość reakcji została użyta dla uproszczenia obliczeń, dając początkowe stężenie substratu Równanie szybkości reakcji (4) może być również zapisane w równaniu (5), które wykorzystuje ujemne i To znacznie ułatwia ustalenie stałych z obliczanych danych (proces, w wyniku którego można narysować wykres Lineweavera-Burka czy wykres Hanesa-Woolfa).
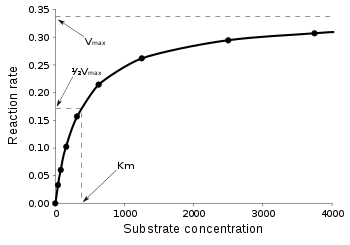
Równanie (4) daje wynik tak zwanej krzywej nasycenia roztworu (wykres po prawej stronie). Graficznie i matematycznie można wyróżnić kilka interesujących sytuacji:
- Gdy stężenie substratu jest duże w porównaniu do wtedy w przybliżeniu Zatem szybkość tworzenia produktu opisana jest równaniem:
- W ten sposób szybkość tworzenia produktu zależy wyłącznie od stężenia enzymu, a równanie przypomina reakcję jednocząsteczkową z odpowiadającą stałą dla pseudopierwszorzędowej reakcji. Zatem nie jest ważne, jak często enzym i substrat ulegają zbliżeniu, tylko jak szybko kompleks [ES] przekształca swój związany substrat w produkt.
- Gdy stężenie substratu wtedy Dlatego szybkość tworzenia produktu opisana jest równaniem
- Gdy stężenie substratu jest małe w porównaniu do wtedy w przybliżeniu i również powstaje niewielka ilość kompleksu ES, więc Dlatego szybkość tworzenia produktu opisana jest wzorem:
- Zatem szybkość tworzenia produktu zależy od stężenia enzymu, jak również od stężenia substratu. Równanie przypomina równanie kinetyczne reakcji drugiego rzędu z odpowiednią stałą szybkości reakcji pseudodrugorzędowej. Ta stała jest miarą wydajności reakcji, tzn. jak wydajnie enzym przetwarza substrat w produkt. Najbardziej wydajne enzymy osiągają w zakresie od 108 – 1010 M−1 s−1, który jest też zakresem dyfuzji. Takie enzymy są tak efektywne, że pozwalają na wydajne katalizowanie reakcji za każdym razem, gdy tylko napotkają cząsteczkę substratu. Można więc uznać, że takie enzymy osiągają górny teoretyczny limit wydajności. Takie enzymy często nazywa się „idealnymi enzymami”.
Uwagi[edytuj | edytuj kod]
- ↑ Stała Michaelisa nie jest stałą równowagi, lecz stosunkiem stałych szybkości reakcji. Dla równania (1) wynosi ona[2]: .
Przypisy[edytuj | edytuj kod]
- ↑ Paweł Kafarski, Barbara Lejczak, Chemia bioorganiczna, Warszawa: Wydawnictwo Naukowe PWN, 1994, s. 16, ISBN 978-83-01-11247-9.
- ↑ a b Michaelis-Menten Treatment of the Kinetic Properties of an Enzyme, [w:] N.V. Bhagavan, Medical biochemistry, wyd. 4, San Diego: Harcourt/Academic Press, 2002, s. 88–91, ISBN 978-0-12-095440-7 (ang.).
Bibliografia[edytuj | edytuj kod]
- Włodzimierz Bednarski, Jan Fiedurk, Podstawy biotechnologii przemysłowej, WNT, Warszawa 2012, ISBN 978-83-63623-42-5.



![{\displaystyle v={\frac {V_{max}[S]}{K_{m}+[S]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aa7dc93224050aab6bb5c872f8bf111e22be796)
![{\displaystyle v=k[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ed4e9e96fb02bfeceb55db4f4c42e8364a7cf2b)




![{\displaystyle ([ES])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f93ba3e45cb79b9f5d7ca51d7baec54b9c13659c)
![{\displaystyle ([P])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4168a3092dde4fe59f0d60e4c07f53019458a314)
![{\displaystyle ([S])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6f4c75ccbedac9d5197d35cc486f28de9e3f1b4)
![{\displaystyle [ES]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31639ab6b9c7c728139b5f8ce03991d800ac7741)
![{\displaystyle {\begin{aligned}{\frac {d[ES]}{dt}}&=k_{1}[E][S]-[ES](k_{-1}+k_{2})\;{\overset {!}{=}}\;0&(2)\\[.5em]{\frac {d[P]}{dt}}&=k_{2}[ES]&(3)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7bd78b8008d7a793a7c17a007df58ad989a7110)
![{\displaystyle ([E]_{0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7db2c3311f9e20fb1fd54c0e05ad88532f575e4)
![{\displaystyle [E]_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/409eb69aba4c3afa67a48af6d9f976a28445c544)
![{\displaystyle [E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a170d18691c57fbfee5802ee401bd9f84ac8804b)
![{\displaystyle [ES]{:}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ce9f1653f16a61682bd848db79de7b170da004b)
![{\displaystyle [E]_{0}=[E]+[ES]\;{\overset {!}{=}}\;{\text{const}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1807cccab3d4ab82eb6262f5189a02bde5d1553)
-[ES](k_{-1}+k_{2})\\k_{1}[S][E]_{0}&=k_{1}[S][ES]+[ES](k_{-1}+k_{2})\\{}[S][E]_{0}&=[S][ES]+[ES]\underbrace {\frac {(k_{-1}+k_{2})}{k_{1}}} _{K_{M}}\\{}[S][E]_{0}&=(K_{M}+[S])[ES]\\{}[ES]&={\frac {[S][E]_{0}}{K_{M}+[S]}}\\\\{\frac {d[P]}{dt}}&=v_{0}=k_{2}[ES]=\underbrace {k_{2}[E]_{0}} _{v_{\max }}{\frac {[S]}{K_{M}+[S]}}\\v_{0}&={\frac {v_{\max[}S]}{K_{M}+[S]}}\;\;\;\;\;\qquad \qquad (4)\\\\{\frac {1}{v_{0}}}&={\frac {K_{M}}{v_{\max }}}\cdot {\frac {1}{[S]}}+{\frac {1}{v_{\max }}}\qquad (5)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d3fd86fac3a8b1720f80d2abe31c6fbe2cc95df)

![{\displaystyle [S].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ce501d93a7280cb9368e3ce9e83eff3d14762c0)
![{\displaystyle [S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/292bbb82029aa583c5d2ac5fa1d7e4fedf537d8b)

![{\displaystyle [S]/(K_{M}+[S])\approx 1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eed6ce4621383a73018d2763b5f02aa1e5b10313)
![{\displaystyle {\frac {d[P]}{dt}}\approx v_{\max }=k_{2}[E]_{0}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfafcb51492e4d50e7698ad6d8333f1621c73ddc)
![{\displaystyle [S]=K_{M}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b30f0140c7cb27f00bd3abe460b121e0dfa17d0)
![{\displaystyle [S]/(K_{M}+[S])=[S]/(2[S])={\frac {1}{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03a52d13d1b3629e505ffa8b3c49668bf940642c)
![{\displaystyle {\frac {d[P]}{dt}}=0,5\cdot v_{\max }=0,5\cdot k_{2}[E]_{0}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75c1643300fcd0c990f414fd63741384095384d2)
![{\displaystyle [S]/(K_{M}+[S])\approx [S]/K_{M}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6824a6225dc4d79d295bbdb8f0517c0dd1f1f1c4)
![{\displaystyle [E]_{0}\approx [E].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04fe1e15933fe4afc4b4214ca21bb458711fb78c)
![{\displaystyle {\frac {d[P]}{dt}}\approx v_{\max }\cdot [S]/K_{M}\approx {\frac {k_{2}}{K_{M}}}[E][S].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08591fe09d2fedbbeac30ea74ca6b553732744e8)

