Hierarchia Chomsky’ego

Zestawy inkluzyjne opisane przez hierarchię Chomsky’ego

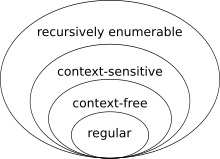
Hierarchia Chomsky’ego – stworzona przez Noama Chomsky’ego hierarchia klas języków formalnych.

Hierarchia składa się z czterech klas:

• języki typu 3 – regularne,
• języki typu 2 – bezkontekstowe,
• języki typu 1 – kontekstowe,
• języki typu 0 – rekurencyjnie przeliczalne.

Język należy do danej klasy wtedy i tylko wtedy, gdy jest możliwe zbudowanie gramatyki formalnej, która generuje dany język, a której reguły nie wykraczają poza ograniczenia dla danej klasy.

Każdy język określonej klasy należy jednocześnie do każdej klasy poniżej, czyli:

• Każdy język regularny jest także bezkontekstowy.
• Każdy język bezkontekstowy jest także kontekstowy.
• Każdy język kontekstowy jest rekurencyjnie przeliczalny.

Zostało także udowodnione, że istnieje teoretyczny algorytm, który jest w stanie przekształcić daną gramatykę formalną w leżącą niżej w hierarchii.

Języki regularne (typu 3)

Język regularny to język, który można wygenerować za pomocą gramatyki liniowej – takiej, która po lewej stronie reguł ma pojedyncze nieterminale, po prawej zaś słowa zawierające co najwyżej jeden nieterminal (jeśli znajduje się on na początku lub na końcu każdego słowa – jest to odpowiednio gramatyka lewostronnie lub prawostronnie liniowa). Poprawne reguły to na przykład:

$A\to \epsilon ,$

$A\to a,$

$A\to abc,$

$A\to B,$

$A\to aB,$

$A\to abcB.$

• Gramatyki liniowe są równoważne automatom skończonym.

Języki bezkontekstowe (typu 2)

Język bezkontekstowy to język, który można wygenerować za pomocą gramatyki bezkontekstowej, która po lewej stronie reguł ma pojedyncze nieterminale, po prawej zaś dowolne słowa, np.:

$A\to aBc,$

$A\to BC,$

a także dowolne reguły gramatyk regularnych.

• jeśli dla danego języka istnieje gramatyka bezkontekstowa, istnieje też równoważna gramatyka bezkontekstowa w postaci normalnej Chomsky’ego i postaci normalnej Greibach.
• Gramatyki bezkontekstowe są równoważne niedeterministycznym automatom ze stosem.

Języki kontekstowe (typu 1)

Język kontekstowy to język, który można wygenerować za pomocą gramatyki kontekstowej, której produkcje są postaci $\alpha A\beta \to \alpha \gamma \beta ,$ gdzie $\alpha$ i $\beta$ są dowolnymi słowami, A jest symbolem nieterminalnym, $\gamma$ – niepustym słowem.

$AB\to CDB$

$AB\to CdEB$

$ABcd\to abCDBcd$

$B\to b$

Dodatkowo pozwala się na regułę postaci $S\to \epsilon ,$ tzn. z symbolu startowego w słowo puste, ale tylko w przypadku jeżeli słowo startowe nie występuje po prawej stronie żadnej reguły.

Nie każda reguła języków bezkontekstowych jest poprawną regułą języków kontekstowych. Reguły postaci $A\to \epsilon$ są dozwolone tylko w tych pierwszych.

• Gramatyki kontekstowe są równoważne automatom liniowo ograniczonym.

Języki rekurencyjnie przeliczalne (typu 0)

Język rekurencyjnie przeliczalny to język, dla którego istnieje gramatyka typu 0, której produkcje są postaci $\alpha \to \beta ,$ gdzie $\alpha$ i $\beta$ są dowolnymi słowami.

• Gramatyki typu 0 są równoważne maszynom Turinga.

Zależności między klasami

Ponieważ (z poprawką na zależność między gramatykami bezkontekstowymi a kontekstowymi) gramatyka typu o mniejszym numerze dopuszcza wszystkie reguły gramatyk o numerze większym, klasy języków kolejnych typów zawierają się w sobie. Zawierania te są ostre, tzn. istnieją języki bezkontekstowe, które nie są regularne, kontekstowe, które nie są bezkontekstowe, oraz rekurencyjnie przeliczalne, które nie są kontekstowe.

Znaczenie

Hierarchia Chomsky’ego wydziela 4 klasy języków, ale możliwe jest stworzenie wielu innych klas, przez odmienne ograniczenia na postać reguł czy inne właściwości języka. Trzy z czterech klas są dość ważne – klasa języków rekurencyjnie przeliczalnych ma dokładnie taką moc jak maszyny Turinga, języki bezkontekstowe odpowiadają niedeterministycznym automatom ze stosem, regularne zaś automatom skończonym.

Bibliografia

• Martin D. Davis, Ron Sigal, Elaine J. Weyuker: Computability, Complexity, and Languages. Morgan Kaufmann Publishers, 1994. ISBN 1-4933-0034-2.