Paradoks Lorda

Ogólny rozkład danych z prostej symulacji paradoksu Lorda. Na osi X waga przed, a na osi Y po okresie stosowania diety.

Paradoks Lorda – pozorny paradoks statystyczny, opisujący sytuację badawczą, której analiza na dwa klasyczne sposoby prowadzi do całkowicie przeciwnych wniosków. Różnica wiąże się z tym, czy i jak badacze kontrolują statystycznie początkowy poziom badanych zmiennych. Jest wariantem paradoksu Simpsona, i ilustruje nadrzędność wnioskowania przyczynowego (założeń oraz pytań dotyczących związków przyczynowych) wobec opisu statystycznego.

Oryginalny opis

Ilustracja pierwszej analizy: zmiany wagi (na osi X) symulowanych obserwacji wewnątrz obu grup mają grupową średnią równą zero.

Ilustracja drugiej analizy: w każdej z grup osobna zmiana wagi (na osi Y) przebiegały w systematyczny sposób w relacji do wagi początkowej (na osi X). W przyjętej tu symulacji zależność odpowiada regresji do średniej, możliwe są także inne związki.

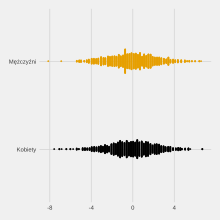
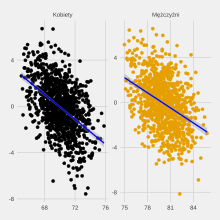
W pierwszej prezentacji problemu z 1967, psychometryk Frederic M. Lord opisał hipotetyczne badanie wpływu diety na wagę studentów, o prostej konstrukcji: 2 grupy (kobiety i mężczyźni) × 2 pomiary wagi (przed i po). Przedstawił przykładowe dane, w których stany wyjściowe w obu grupach: ${\bar {X}}_{a},{\bar {X}}_{b},$ i stany końcowe: ${\bar {Y}}_{a},{\bar {Y}}_{b},$ charakteryzuje równa różnica: ${\bar {Y}}_{b}-{\bar {Y}}_{a}={\bar {X}}_{b}-{\bar {X}}_{a}=D.$ Opisał następnie dwa możliwe, poprawne arytmetycznie, sposoby analizy takich danych, prowadzące do sprzecznych wniosków. Uznał, że oba podejścia mogą być prawidłowe, nie proponując rozwiązania paradoksu – klarownej reguły co do tego, którą metodę wybierać w jakich sytuacjach.

Pierwsza analiza skupia się na tym, że średnia waga w każdej grupie, oraz różnica średnich wag pomiędzy grupami, pozostaje identyczna w obu pomiarach – co prowadzi do konkluzji o braku zmiany, którą można potwierdzić np. testem t Studenta lub analizą wariancji, i co można interpretować jako „diety nie różnią się efektywnością”:

$({\bar {Y}}_{b}-{\bar {X}}_{b})-({\bar {Y}}_{a}-{\bar {X}}_{a})=({\bar {Y}}_{b}-{\bar {Y}}_{a})-({\bar {X}}_{b}-{\bar {X}}_{a})=D-D=0$.

Druga analiza bierze poprawkę na początkową wagę w obu grupach, np. przez analizę kowariancji. Choć średnie w obu grupach nie zmieniły się, to indywidualne wagi nie musiały pozostać identyczne. O ile tak się nie stało – jak implicite zakłada Lord – i ich korelacja nie jest całkowita, $r\neq 1,$ to podejście wykrywa pewną różnicę, którą można interpretować jako „diety mają wpływ na zmianę wagi”:

$({\bar {Y}}_{b}-{\bar {Y}}_{a})-r({\bar {X}}_{b}-{\bar {X}}_{a})=D-rD=(1-r)D\neq 0$.

Lord przedstawił w następnych latach kilka dodatkowych przykładów o tej podobnej strukturze. Skłaniał się stopniowo do przekonania, że w oryginalnym scenariuszu niewłaściwe było drugie podejście, i przestrzegał przed nieostrożnym stosowaniem analizy kowariancji.

Odpowiedzi

Pozorny paradoks przyciągnął szereg prób rozwiązania, oraz rozwinięcia i uzupełnienia problemu. Odnieśli się do niego między innymi autorzy dwóch spośród głównych współczesnych podejść do wnioskowania przyczynowego – Donald Rubin i Judea Pearl.

Holland i Rubin

Holland i Rubin omówili paradoks Lorda w 1982. Zgodzili się, że obie analizy są równie poprawne jako statystyczny opis stanu rzeczy. Zaznaczyli jednak, że badanie, które nie zawiera randomizowanej manipulacji eksperymentalnej (lub jej quasi-eksperymentalnego przybliżenia), i nie tworzy grupy kontrolnej i grupy eksperymentalnej (lub ich odpowiednika), nie daje samo w sobie podstawy do wyciągania wniosków o związkach przyczynowych. Podstawowym problemem przykładu Lorda jest więc brak grup kontrolnych przy wszystkich branych pod uwagę zmiennych objaśniających. Brak ten można próbować załagodzić przez przyjęcie dodatkowych założeń, jednak różne założenia pozwalają na uzasadnienie obu przedstawionych analiz, i – ponieważ bez grupy kontrolnej nie da się ich przetestować – nie można pomiędzy nimi rozstrzygnąć. Scenariusz przedstawiony przez Lorda opisuje zatem jedynie źle zaprojektowane badanie.

Pearl

Pearl przedstawił swoją ocenę paradoksu m.in. w publikacji z 2016 i książce z 2018. Pearl wyraził także przekonanie, że konstrukcja badania nie pozwala na ogólne porównanie efektu obu diet. Uznał jednak, że sam Lord był tego świadomy i zadaniem analizy miała być ocena różnicowego efektu konkretnej diety w obu grupach. Zdaniem Pearla, pierwsza analiza jest w tym przypadku prawidłowa, ponieważ waga początkowa jest mediatorem efektu płci i nie należy jej kontrolować. Uznał za błąd Hollanda i Rubina przyjęcie, że ponieważ płeć nie poddaje się randomizowaniu, to oryginalny scenariusz jest całkowicie nieinformatywny. Zaznaczył także, że gdyby diety nie były przydzielane według płci ale w losowy sposób, struktura przyczynowa badania byłaby zupełnie inna i to drugie podejście byłoby właściwe.

Znaczenie

Odwołujące się do paradoksu Lorda krytyki metodologii badań stosujących lub rezygnujących z analizy kowariancji opublikowano m.in. w psychologii poznawczej i różnic indywidualnych, medycynie, psychiatrii i psychologii klinicznej czy w pedagogice.