Moment zatrzymania
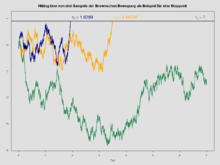
Moment zatrzymania – specjalnego typu zmienna losowa, używana w teorii prawdopodobieństwa, a w szczególności przy badaniu procesów stochastycznych.
Reguła zatrzymania czy też momenty zatrzymania są analizowane i wykorzystywane zarówno w teorii prawdopodobieństwa, jak i statystyce, w szczególności przy próbkowaniu ciągów losowych czy w analizie sekwencyjnej. Często momenty zatrzymania są wykorzystywane w technikach dowodzenia twierdzeń metodą „temperowania czasu ciągłego” (szczegóły są w monografii Chunga (1982)).
Definicja[edytuj | edytuj kod]
Moment zatrzymania dla ciągu zmiennych losowych to zmienna losowa o własności takiej, że dla każdego to czy zdarzenie zrealizowało się, zależy wyłącznie od realizacji zmiennych losowych a ponadto tj. jest prawie wszędzie skończona. Jeśli skończoność zmiennej losowej nie jest wymagana, to mówimy o markowskim momencie zatrzymania. Momenty zatrzymania pojawiają się w teorii decyzji, gdzie reguła zatrzymania jest strategią wskazującą moment zatrzymania obserwacji procesu na podstawie aktualnego i przeszłych stanów procesu w celu zrealizowania założonego celu.
Inna definicja, bardziej ogólna, wykorzystuje pojęcie filtracji. Niech będzie uporządkowanym zbiorem indeksów (często lub zwarty podzbiór tego przedziału). jest przestrzenią probabilistyczną z filtracją, to znaczy, jest to przestrzeń probabilistyczna ze zdefiniowaną wstępującą rodziną -algebr zwaną filtracją. Wówczas zmienna losowa jest momentem Markowa, jeśli dla każdego Często, aby uniknąć nieporozumień, mówimy o takiej zmiennej losowej iż jest -momentem markowskim. Jeśli dodatkowo moment Markowa jest skończony z prawdopodobieństwem to nazywamy go momentem zatrzymania.
Inaczej mówiąc, aby był momentem markowskim powinno być możliwe stwierdzenie, czy zrealizowało się na podstawie
Przykłady[edytuj | edytuj kod]
W celu ilustracji podamy przykłady zmiennych losowych które są momentami zatrzymania i takich, które nie spełniają definicji. Rozważmy hazardzistę grającego w ruletkę z kapitałem początkowym 100 $:
- Grając tylko jeden raz, realizujemy moment zatrzymania
- Momentem zatrzymania jest strategia „graj co najwyżej 500 razy lub do wyczerpania pieniędzy”.
- Strategia gracza „gram do podwojenia kapitału początkowego (i pożyczam jeśli trzeba)” nie jest momentem zatrzymania, jako że istnieje dodatnie prawdopodobieństwo tego, że nigdy nie zrealizujemy zamierzonego celu.
- Strategia gracza „gram do podwojenia kapitału lub do chwili bankructwa” jest momentem zatrzymania ponieważ zatrzymujemy się z prawdopodobieństwem jeden w skończonym czasie.
Lokalizacja[edytuj | edytuj kod]
Momenty zatrzymania są często wykorzystywane do uogólniania pewnych własności procesów stochastycznych na przypadek w którym żądana własność jest spełniona jedynie lokalnie. Niech będzie procesem a momentem zatrzymania. Wówczas oznaczenie wykorzystujemy do oznaczenia procesu zatrzymanego w chwili
Wówczas mówimy, że ma lokalnie własność jeśli istnieje ciąg momentów zatrzymania rosnących do nieskończoności i dla których procesy mają własność Przykłady, dla procesów indeksowanych elementami zbioru są następujące;
- (Lokalny martyngał) Proces jest lokalnym martyngałem, jeśli ma własność càdlàg (trajektorie są prawostronnie ciągłe i posiadają lewostronna granicę) i istnieje rosnący do nieskończoności ciąg momentów zatrzymania taki, że jest martyngałem dla każdego
- (Lokalna całkowalność) Nieujemny i rosnący proces jest lokalnie całkowalny, jeśli istnieje ciąg momentów zatrzymania rosnący do nieskończoności taki, że dla każdego
Typy momentów zatrzymania[edytuj | edytuj kod]
Momenty zatrzymania o wartościach w dzielmy często na typy ze względu na to, czy jest możliwe przewidywanie ich realizacji.
Moment zatrzymania jest przewidywalny jeśli jest granicą rosnącego ciągu momentów zatrzymania o własności, iż gdy O ciągu mówimy, że anonsuje a zatem przewidywalny moment zatrzymania jest w tym sensie prognozowalny. Przykładem przewidywalnego momentu zatrzymania jest moment pierwszego osiągnięcia dla procesu ciągłego i uzgodnionego. Jeśli jest pierwszą chwilą w której ciągły, rzeczywisty proces jest równy pewnej wartości to ciągiem anonsującym jest gdzie jest pierwszą chwilą w której jest w odległości od
Osiągalny moment zatrzymania to taki, który może być „przykryty” przez przewidywalne momenty zatrzymania. To znaczy, że moment zatrzymania jest osiągalny, jeśli dla pewnego gdzie są momentami przewidywalnymi.
Moment zatrzymania jest całkowicie nieosiągalny jeśli nie może być nigdy „anonsowany” przez rosnący ciąg momentów zatrzymania. Równoważnie, dla każdego przewidywalnego momentu Przykładem całkowicie nieosiągalnych momentów zatrzymania są chwile skoków procesu Poissona.
Każdy moment markowski może być w jedyny sposób rozłożony na osiągalny i nieosiągalny moment markowski. To oznacza, że istnieją jedyne osiągalny moment markowski oraz całkowicie nieosiągalny moment markowski takie, że:
- gdy
- gdy
- gdy
Zobacz też[edytuj | edytuj kod]
Literatura[edytuj | edytuj kod]
- Kai Lai Chung: Lectures from Markov processes to Brownian motion. New York: Springer-Verlag, 1982, seria: Grundlehren der Mathematischen Wissenschaften No. 249. ISBN 0-387-90618-5.
- Jakubowski, Jacek; Sztencel, R.: Wstęp do teorii prawdopodobieństwa. Warszawa: SCRIPT, 2000. ISBN 83-904564-4-3.
- Revuz, Daniel and Yor, Marc: Continuous martingales and Brownian motion. Wyd. Third edition. Berlin: Springer-Verlag, 1999, seria: Grundlehren der Mathematischen Wissenschaften No. 293. ISBN 3-540-64325-7.
- Philip E. Protter: Stochastic integration and differential equations. Wyd. Second edition (version 2.1, corrected third printing). Berlin: Springer-Verlag, 2005, seria: Stochastic Modelling and Applied Probability No. 21. ISBN 3-540-00313-4.
Literatura uzupełniająca[edytuj | edytuj kod]
- Thomas S. Ferguson, Who solved the secretary problem?, „Stat. Sci.”, 4, 1989, s. 282–296, ISBN 3-540-74010-4, JSTOR: 2245639.
- Albert N. Shiryaev: Optimal Stopping Rules. Springer, 2007. ISBN 3-540-74010-4.














































