Funkcje Kelvina – funkcje powiązane z funkcjami Bessela zespolonego argumentu. Oznaczane są symbolami:
b
e
r
ν
z
{\displaystyle \mathrm {ber} _{\nu }z}
b
e
i
ν
z
{\displaystyle \mathrm {bei} _{\nu }z}
ker
ν
z
{\displaystyle \ker _{\nu }z}
k
e
i
ν
z
{\displaystyle \mathrm {kei} _{\nu }z}
h
e
r
ν
z
{\displaystyle \mathrm {her} _{\nu }z}
h
e
i
ν
z
{\displaystyle \mathrm {hei} _{\nu }z}
gdzie
z
{\displaystyle z}
ν
{\displaystyle \nu }
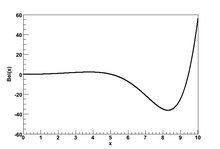
Ber(x ) for x between 0 and 10.
b
e
r
(
x
)
/
e
x
/
2
{\displaystyle \mathrm {ber} (x)/e^{x/{\sqrt {2}}}}
x
{\displaystyle x}
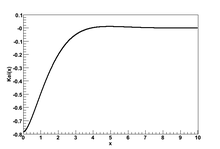
Bei(x) for
x
{\displaystyle x}
B
e
i
(
x
)
/
e
x
/
2
{\displaystyle \mathrm {Bei} (x)/e^{x/{\sqrt {2}}}}
x
{\displaystyle x}
Ker(x) for
x
{\displaystyle x}
K
e
r
(
x
)
e
x
/
2
{\displaystyle \mathrm {Ker} (x)e^{x/{\sqrt {2}}}}
x between 0 and 100.Kei(x) for
x
{\displaystyle x}
K
e
i
(
x
)
e
x
/
2
{\displaystyle \mathrm {Kei} (x)e^{x/{\sqrt {2}}}}
x
{\displaystyle x}
Funkcje
b
e
r
ν
z
{\displaystyle \mathrm {ber} _{\nu }z}
b
e
i
ν
z
{\displaystyle \mathrm {bei} _{\nu }z}
J
ν
(
…
)
{\displaystyle J_{\nu }(\dots )}
3
π
i
/
4
{\displaystyle 3\pi i/4}
i
{\displaystyle i}
jednostką urojoną :
J
m
(
e
±
3
π
i
/
4
z
)
=
b
e
r
ν
z
±
i
b
e
i
ν
z
{\displaystyle J_{m}(e^{\pm 3\pi i/4}z)=\mathrm {ber} _{\nu }z\pm i\,\mathrm {bei} _{\nu }z}
Alternatywną definicją jest:
e
ν
π
i
/
2
I
ν
(
e
π
i
/
4
z
)
=
b
e
r
ν
z
+
i
b
e
i
ν
z
{\displaystyle e^{\nu \pi i/2}I_{\nu }(e^{\pi i/4}z)=\mathrm {ber} _{\nu }z+i\,\mathrm {bei} _{\nu }z}
gdzie
I
ν
(
…
)
{\displaystyle I_{\nu }(\dots )}
zmodyfikowaną funkcją Bessela pierwszego rodzaju rzędu rzeczywistego.
Funkcje
ker
ν
z
{\displaystyle \ker _{\nu }z}
k
e
i
ν
z
{\displaystyle \mathrm {kei} _{\nu }z}
e
ν
π
i
/
2
{\displaystyle e^{\nu \pi i/2}}
zmodyfikowanej funkcji Bessela drugiego rodzaju rzędu rzeczywistego
K
ν
(
…
)
{\displaystyle K_{\nu }(\dots )}
e
π
i
/
4
:
{\displaystyle e^{\pi i/4}{:}}
e
−
ν
π
i
/
2
K
ν
(
e
π
i
/
4
z
)
=
ker
ν
z
+
i
k
e
i
ν
z
{\displaystyle e^{-\nu \pi i/2}K_{\nu }(e^{\pi i/4}z)=\ker _{\nu }z+i\,\mathrm {kei} _{\nu }z}
Funkcje
h
e
r
ν
z
{\displaystyle \mathrm {her} _{\nu }z}
h
e
i
ν
z
{\displaystyle \mathrm {hei} _{\nu }z}
funkcji Hankela I rodzaju rzędu rzeczywistego
H
ν
(
1
)
(
…
)
{\displaystyle H_{\nu }^{(1)}(\dots )}
e
3
π
i
/
4
:
{\displaystyle e^{3\pi i/4}{:}}
H
ν
(
1
)
(
e
±
3
π
i
/
4
z
)
=
h
e
r
ν
z
±
i
h
e
i
ν
z
{\displaystyle H_{\nu }^{(1)}(e^{\pm 3\pi i/4}z)=\mathrm {her} _{\nu }z\pm i\,\mathrm {hei} _{\nu }z}
W zapisie rząd zerowy funkcji Kelvina opuszcza się, tj. mamy:
J
0
(
i
±
3
/
2
z
)
=
b
e
r
z
±
i
b
e
i
z
{\displaystyle J_{0}(i^{\pm 3/2}z)=\mathrm {ber} \,z\pm i\,\mathrm {bei} \,z}
J
0
(
i
i
z
)
=
b
e
r
z
±
i
b
e
i
z
{\displaystyle J_{0}(i{\sqrt {i}}\,z)=\mathrm {ber} \,z\pm i\,\mathrm {bei} \,z}
J
0
(
e
±
3
π
i
/
4
z
)
=
b
e
r
z
+
i
b
e
i
z
{\displaystyle J_{0}(e^{\pm 3\pi i/4}z)=\mathrm {ber} \,z+i\,\mathrm {bei} \,z}
J
0
(
e
−
π
i
/
4
z
)
=
b
e
r
z
+
i
b
e
i
z
{\displaystyle J_{0}(e^{-\pi i/4}z)=\mathrm {ber} \,z+i\,\mathrm {bei} \,z}
K
0
(
i
±
1
/
2
z
)
=
ker
z
±
i
k
e
i
z
{\displaystyle K_{0}(i^{\pm 1/2}z)=\ker \,z\pm i\,\mathrm {kei} \,z}
K
0
(
i
z
)
=
ker
z
+
i
k
e
i
z
{\displaystyle K_{0}({\sqrt {i}}\,z)=\ker \,z+i\,\mathrm {kei} \,z}
K
0
(
−
i
z
)
=
ker
z
−
i
k
e
i
z
{\displaystyle K_{0}({\sqrt {-i}}\,z)=\ker \,z-i\,\mathrm {kei} \,z}
H
0
(
1
)
(
i
+
3
/
2
z
)
=
h
e
r
z
+
i
h
e
i
z
{\displaystyle H_{0}^{(1)}(i^{+3/2}z)=\mathrm {her} \,z+i\,\mathrm {hei} \,z}
Funkcje Kelvina są rzeczywiste dla rzeczywistych wartości argumentu
z
.
{\displaystyle z.}
z
=
0
{\displaystyle z=0}
b
e
r
n
z
{\displaystyle \mathrm {ber} _{n}z}
b
e
i
n
z
{\displaystyle \mathrm {bei} _{n}z}
Między funkcjami Kelvina zachodzą związki:
ker
ν
z
=
−
π
2
h
e
i
ν
z
{\displaystyle \ker _{\nu }z=-{\frac {\pi }{2}}\,\mathrm {hei} _{\nu }z}
k
e
i
ν
z
=
1
2
h
e
r
ν
z
{\displaystyle \mathrm {kei} _{\nu }z={\frac {1}{2}}\,\mathrm {her} _{\nu }z}
Funkcje
b
e
r
z
,
b
e
i
z
,
h
e
r
z
,
h
e
i
z
,
{\displaystyle \mathrm {ber} \,z,\,\mathrm {bei} \,z,\,\mathrm {her} \,z,\,\mathrm {hei} \,z,}
d
2
f
(
z
)
d
z
2
+
1
z
d
f
(
z
)
d
z
−
i
f
(
z
)
=
0
{\displaystyle {\frac {d^{2}f(z)}{dz^{2}}}+{\frac {1}{z}}\,{\frac {df(z)}{dz}}-i\,f(z)=0}
Natomiast funkcje
b
e
r
ν
z
,
b
e
i
ν
z
,
h
e
r
ν
z
,
h
e
i
ν
z
,
{\displaystyle \mathrm {ber} _{\nu }z,\,\mathrm {bei} _{\nu }z,\,\mathrm {her} _{\nu }z,\,\mathrm {hei} _{\nu }z,}
d
2
f
(
z
)
d
z
2
+
1
z
d
f
(
z
)
d
z
−
(
i
+
ν
2
z
2
)
f
(
z
)
=
0
{\displaystyle {\frac {d^{2}f(z)}{dz^{2}}}+{\frac {1}{z}}\,{\frac {df(z)}{dz}}-\left(i+{\frac {\nu ^{2}}{z^{2}}}\right)\,f(z)=0}
Dla funkcji
b
e
r
n
z
{\displaystyle \mathrm {ber} _{n}\,z}
n
{\displaystyle n}
b
e
r
n
z
=
(
z
2
)
n
∑
k
=
0
∞
cos
[
(
3
n
4
+
k
2
)
π
]
k
!
Γ
(
n
+
k
+
1
)
(
z
2
4
)
k
{\displaystyle \mathrm {ber} _{n}\,z=\left({\frac {z}{2}}\right)^{n}\sum _{k=0}^{\infty }{\frac {\cos \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]}{k!\,\Gamma (n+k+1)}}\left({\frac {z^{2}}{4}}\right)^{k}}
gdzie Γ(z ) jest funkcją gamma .
W przypadku funkcji
b
e
r
z
{\displaystyle \mathrm {ber} \,z}
b
e
r
(
z
)
=
1
+
∑
k
=
1
∞
(
−
1
)
k
(
z
/
2
)
4
k
[
(
2
k
)
!
]
2
{\displaystyle \mathrm {ber} (z)=1+\sum _{k=1}^{\infty }{\frac {(-1)^{k}(z/2)^{4k}}{[(2k)!]^{2}}}}
tj.:
b
e
r
(
z
)
=
1
−
1
(
2
!
)
2
(
z
2
)
4
+
1
(
4
!
)
2
(
z
2
)
8
−
…
{\displaystyle \mathrm {ber} (z)=1-{\frac {1}{(2!)^{2}}}\,\left({\frac {z}{2}}\right)^{4}+{\frac {1}{(4!)^{2}}}\,\left({\frac {z}{2}}\right)^{8}-\ldots }
Dla funkcji
b
e
i
n
z
{\displaystyle \mathrm {bei} _{n}\,z}
n
{\displaystyle n}
b
e
i
n
z
=
(
z
2
)
n
∑
k
=
0
∞
sin
[
(
3
n
4
+
k
2
)
π
]
k
!
Γ
(
n
+
k
+
1
)
(
z
2
4
)
k
{\displaystyle \mathrm {bei} _{n}\,z=\left({\frac {z}{2}}\right)^{n}\sum _{k=0}^{\infty }{\frac {\sin \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]}{k!\,\Gamma (n+k+1)}}\left({\frac {z^{2}}{4}}\right)^{k}}
gdzie Γ(z ) jest funkcją gamma .
W przypadku funkcji
b
e
i
z
{\displaystyle \mathrm {bei} \,z}
b
e
i
(
z
)
=
∑
k
=
0
∞
(
−
1
)
k
(
z
/
2
)
4
k
+
2
[
(
2
k
+
1
)
!
]
2
{\displaystyle \mathrm {bei} (z)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(z/2)^{4k+2}}{[(2k+1)!]^{2}}}}
tj.
b
e
i
(
z
)
=
(
z
2
)
2
−
1
(
3
!
)
2
(
z
2
)
6
+
1
(
5
!
)
2
(
z
2
)
10
−
…
{\displaystyle \mathrm {bei} (z)=\left({\frac {z}{2}}\right)^{2}-{\frac {1}{(3!)^{2}}}\,\left({\frac {z}{2}}\right)^{6}+{\frac {1}{(5!)^{2}}}\,\left({\frac {z}{2}}\right)^{10}-\ldots }
Watson: A Traetise on the Theory of Bessel Functions , Cambridge University Press, Cambridge.
Olver F.W., Maximin L.C.: Bessel Functions .
Lozier D.M., et al.: NIST Hanbook of Mathematical Functions , Cambridge University Press, Cambridge.
Gradshteyn I.S., Ryzhik I.M.: Tablitsy integralov, ryadov, summ i proizvedeniy , Moskva, (1971).
Korn G.A., Korn T.M.: Mathematical Handbook for Scientists and Engineers , McGraw-Hill. 




















































![{\displaystyle \mathrm {ber} _{n}\,z=\left({\frac {z}{2}}\right)^{n}\sum _{k=0}^{\infty }{\frac {\cos \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]}{k!\,\Gamma (n+k+1)}}\left({\frac {z^{2}}{4}}\right)^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9816ab295102516738bbdb7e4bd8e88bec81d7ea)

![{\displaystyle \mathrm {ber} (z)=1+\sum _{k=1}^{\infty }{\frac {(-1)^{k}(z/2)^{4k}}{[(2k)!]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcf35c5fe9f0ace4e6204de5502aa3b25b394533)


![{\displaystyle \mathrm {bei} _{n}\,z=\left({\frac {z}{2}}\right)^{n}\sum _{k=0}^{\infty }{\frac {\sin \left[\left({\frac {3n}{4}}+{\frac {k}{2}}\right)\pi \right]}{k!\,\Gamma (n+k+1)}}\left({\frac {z^{2}}{4}}\right)^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/528bd84a7cf4afdf6374f414075aaf063da005ee)

![{\displaystyle \mathrm {bei} (z)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(z/2)^{4k+2}}{[(2k+1)!]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9ad6575f22eed242d02106d6e0b87be1c105763)
