Sylogizm

Sylogizm (z stgr. συλλογισμός – konkluzja, wniosek) jest to wnioskowanie o dwóch przesłankach, przy czym obie przesłanki zawierają wspólny element, a każdy element wniosku zawarty jest w dokładnie jednej przesłance.

Sylogizm Arystotelesa

Sylogizm wywodzi się z prac Arystotelesa, który jako pierwszy podał jego przykład, znany właśnie jako sylogizm Arystotelesa. Jego sformułowanie uważane jest za początek klasycznej logiki. Najczęściej przywoływany jest w postaci:

Jeżeli każdy M jest P oraz każdy P jest S, to każdy M jest S.

Przytoczone powyżej zdanie jest prawdziwe niezależnie od tego, czy za "każdy M jest P" lub "każdy P jest S" podstawimy prawdę czy fałsz. Np. jeżeli powiemy: Jeżeli każdy człowiek jest drzewem i każde drzewo jest rośliną, to każdy człowiek jest rośliną, całość będzie zdaniem prawdziwym, pomimo że np. przesłanka każdy człowiek jest drzewem jest oczywiście fałszywa.

Przykłady

Poniżej zaprezentowano schematy figur sylogistycznych różnych trybów. Przykładowo tryb "Barbara" zgodnie ze schematem mówi, iż "Każde M jest P, każde S jest M, więc każde S jest P". Należy więc wyjaśnić dlaczego jest zapisywany w takiej formie. Jak stwierdził Oktawian Nawrot, "sylogistyka, zwana również tradycyjną logiką nazw, tradycyjnym rachunkiem nazw lub tradycyjną logiką zdań kategorycznych, jest najstarszym systemem logicznym, za którego twórcę uważa się Arystotelesa. System ten na przestrzeni wieków nie uległ znaczącym zmianom...". Ułatwia to tym samym zrozumienie i układanie sylogizmów.

Sylogistyka to teoria związków zachodzących między tzw. zdaniami kategorycznymi. Kategorycznymi, to znaczy o budowie podmiotowo-orzecznikowej. Każde zdanie winno więc zawierać podmiot i orzecznik. W tradycyjnej logice zdań wyróżnia się cztery takie zdania, które są obrazowane następującymi symbolami:

1. S a P
2. S e P
3. S i P
4. S o P

S to podmiot (od łac. subiectum), P to orzecznik (łac. predicatum). W miejsce S i P należy podstawiać w sylogistyce zdania prawidłowe logicznie, tj. takie o których można powiedzieć, czy są prawdziwe czy fałszywe. Natomiast nazwy w zdaniu pełnią w sylogistyce rolę terminów (łac. terminus). Powinny być to nazwy niepuste, tj. posiadające realnie istniejące desygnaty. Zaś symbole "a", "e", "i", "o", to stałe logiczne, za pomocą których zdania są konstruowane. Stałe "a" oraz "i" oznaczają zdania twierdzące. Pochodzi to od łacińskiego słowa affirmo - twierdzę. Natomiast stałe "e" oraz "o" określają zdania przeczące - od wyrazu "nego" - przeczę.

Zatem zdanie "M a P" będzie zdaniem kategorycznym twierdzącym. Odczytujemy je jako "Każde M jest P". Jeśli w miejsce M i P wstawimy nazwy niepuste, to otrzymamy np. "Każda wikipedystka jest kobietą". Natomiast używając stałej "i", ułożymy zdanie "P i M", które będzie oznaczało "Niektóre kobiety są wikipedystkami". W trybach sylogistycznych ważne jest prześledzenie, jak zachodzą na siebie zakresy nazwowe poszczególnych nazw. W tym przypadku kobiet i wikipedystek.

Terminy również pełnią specjalne funkcje. S to termin mniejszy (terminus minor); P to termin większy (terminus maius); M to termin średni (terminus medinus). Sylogizm jest zbudowany hierarchicznie: u góry przesłanka większa (z terminem P), poniżej jest przesłanka mniejsza (z terminem S), a pod kreską wniosek. Sylogizmy układają się w figury i tryby, zależnie od położenia terminów. Wyróżnia się cztery podstawowe figury (I, II, III, IV), które różnią się położeniem terminu średniego "M". Dla każdej z figur można zbudować 64 tryby, przesuwając termin średni i manipulując stałymi (a, e, i, o). Łącznie więc można otrzymać aż 256 trybów. Jednakże tylko część z nich jest trybami logicznie poprawnymi (tj. słusznymi). Dlatego też sprowadzono je do 24 trybów słusznych, po sześć w obrębie każdej z figur.

Tryb "Barbara" zalicza się do trybów słusznych I figury. Powstaje według schematu:

M a P
S a M
-----
S a P

Obrazuje to schemat:

przesłanka większa (ponieważ zawiera termin większy)
przesłanka mniejsza (z terminem mniejszym)
-------------------
wniosek

Jak widać termin "M" występuje w przesłankach, ale nie we wniosku. Należy pamiętać, iż przesłanka większa jest zapisywana jako pierwsza (najwyżej). Poniżej umieszcza się przesłankę mniejszą. Dlatego też sylogizm oznacza, jak już wyżej wspomniano: "Każde M jest P, każde S jest M, więc każde S jest P". Nazywa się ten tryb "Barbara", ponieważ składa się z trzech stałych "a" (Barbara) i w średniowieczu, dla ułatwienia zapamiętania trybów ułożono sobie wierszyk:

Barbara, Celarent, Darii, Ferioque prioris;
Cesare, Camestres, Festino, Baroco sedundae;
tertia Darapti, Disamis, Datisi, Felapton;
Bocardo, Ferison habet; quarta insuper addit
Bamalip, Camenes, Dimatis, Fesapo, Fresison.

Pozostałe tryby przedstawione są w tabeli poniżej, ułożone przy pomocy diagramów Venna, zgodnie z figurami:

I figura	Barbara	Barbari	Celarent	Celaront	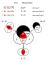Darii	Ferio
II figura	Cesare	Cesaro	Camestres	Camestros	Festino	Baroco
III figura	Darapti	Disamis	Datisi	Felapton	Bocardo	Ferison
IV figura	Bamalip	Calemes	Calemos	Dimatis	Fesapo	Fresison

Zobacz też

• Antylogizm
• Kwadrat logiczny
• Logika prawnicza
• Teoria nazw