Układ całkujący
Integrator – ogólnie, urządzenie do całkowania numerycznego lub graficznego (zob. integraf, integrometr); we współczesnym słownictwie technicznym raczej rodzaj całkującego układu elektronicznego (obwód prądu zmiennego, w którym napięcie wyjściowe jest proporcjonalne do całki oznaczonej z napięcia wejściowego).

Idealny układ całkujący odpowiada na sygnał wejściowy sygnałem według zależności:
Odpowiedzią idealnego układu całkującego na impuls Diraca jest skok jednostkowy. Odpowiedzią idealnego układu całkującego na wartość stałą jest funkcja liniowo zmienna.
Dobrym przybliżeniem układu całkującego jest układ ze wzmacniaczem operacyjnym, pokazany na rysunku.
Dowód[edytuj | edytuj kod]
Prąd płynący przez rezystor R
Prąd płynący przez kondensator C
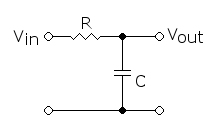
W żargonie elektronicznym układem całkującym bywa nazywany układ inercyjny pierwszego rzędu złożony z rezystora i kondensatora. W rzeczywistości, napięcie na wyjściu układu (napięcie na kondensatorze) jest opisane równaniem całkowym:
Układ RC zachowuje się zatem jak układ całkujący jedynie w sytuacji gdy kondensator jest rozładowany, czyli gdy












