Centroid

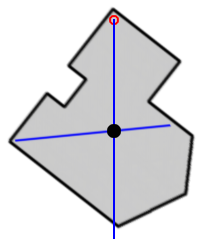
Centroid – punkt związany z obszarem, w szczególności z wielokątem, leżący wewnątrz niego, reprezentujący geometryczne uściślenie intuicyjnego "środka" obszaru.

Grafika komputerowa

Pojęcie to zrobiło karierę z rozwojem grafiki komputerowej, zwłaszcza w dziedzinie systemów informacji przestrzennej (np. GIS) i kartografii. W systemach tych centroid służy m.in. jako punkt zaczepienia informacji tekstowych związanych z obszarem, np. do umieszczenia nazwy państwa w "środku" obszaru państwa, numeru domu w obrysie budynku, itp.

Dla wielokątów wypukłych centroidem jest środek geometryczny ("środek masy") figury. Ta reguła nie wystarcza jednak w przypadku wielokątów wklęsłych (tj. mających co najmniej jeden kąt większy od 180°) – środek geometryczny takiego wielokąta może leżeć poza wielokątem. Wówczas za centroid przyjmuje się według różnych kryteriów punkt względnie bliski środka masy, jednak leżący wewnątrz wielokąta.

Pojęcie to jest również używane w grafice trójwymiarowej, na przykład przy wykrywaniu kolizji oraz renderowaniu scen dynamicznych metodą śledzenia promieni.

Statystyka

W statystyce pojęcie centroidu stosowane jest w analizie skupień. Centroid jest swego rodzaju reprezentantem danego skupienia, przydatnym szczególnie przy interpretacji wyników analizy w formie zrozumiałej dla klienta. Można wówczas wybrać typowego reprezentanta każdego ze skupień i po sprawdzeniu jego cech nadać nazwę całemu skupieniu, np. "yuppies", albo "spełnione rodziny". To podejście nie ma sensu, jeśli jest zastosowane do zbyt niejednorodnych grup – np. pojęcie "typowego Polaka" nie ma sensu, w szczególności trudno byłoby dobrać jego płeć.

Na centroidach opierają się też niektóre metody hierarchicznej analizy skupień, np. niektóre odmiany k-mean clustering, gdzie coraz większe skupienia są w kolejnych krokach analizy zastępowane swoimi centroidami.