Paradoksy Zenona z Elei

Paradoksy Zenona z Elei – zbiór kilku paradoksów pochodzących od greckiego filozofa, Zenona z Elei. Są to paradoksy, które łączy ukazanie trudności w rozumieniu czasu i przestrzeni jako wielkości ciągłych, które można w związku z tym dzielić w nieskończoność. Oprócz znaczenia czysto filozoficznego, paradoksy te mają też znaczenie matematyczne i fizyczne.

Paradoksy ruchu

Miały na celu udowodnienie, że ruch w świecie, który postrzegamy, jest jedynie złudzeniem, które nie jest możliwe w rzeczywistości. Cztery z nich przekazał Arystoteles w swojej Fizyce.

Dychotomia

• 
• 

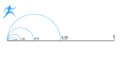
Sprinter ma do przebiegnięcia skończony dystans. Zanim jednak pokona całą odległość, musi najpierw dobiec do 1/2 długości, ale zanim dobiegnie do 1/2, musi najpierw dobiec do 1/4, ale zanim dobiegnie do 1/4, musi najpierw dobiec do 1/8, i tak w nieskończoność. Wynika z tego, że biegacz ma do przebycia nieskończoną liczbę odcinków o skończonej długości. Ponieważ nie da się pokonać nieskończonej liczby odcinków w skończonym czasie, biegacz nigdy nie ukończy biegu.

Co więcej, biegacz nie może nawet zacząć biegu, bo ten sam paradoks stosuje się również do dystansu dowolnie zmniejszonego: tak samo, jak nie da się (według powyższego rozumowania) dobiec na dystans 100 m, nie da się również na dystans jednego metra ani na dystans jednego milimetra.

$\sum _{n=1}^{\infty }{\frac {1}{2^{n}}}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\ldots +{\frac {1}{2^{n}}}+\ldots$

Achilles i żółw

Odległość w czasie, przy założeniu, że żółw ucieka z połową prędkości Achillesa

Achilles i żółw

Achilles i żółw stają na linii startu wyścigu na dowolny, skończony dystans. Achilles potrafi biegać 2 razy szybciej od żółwia i dlatego na starcie pozwala oddalić się żółwiowi o 1/2 całego dystansu. Achilles, jako biegnący 2 razy szybciej od żółwia, dobiegnie do 1/2 dystansu w momencie, gdy żółw dobiegnie do 3/4 dystansu. W momencie gdy Achilles przebiegnie 3/4 dystansu, żółw znowu mu „ucieknie”, pokonując 7/8 dystansu. Gdy Achilles dotrze w to miejsce, żółw znowu będzie od niego o 1/16 dystansu dalej, i tak w nieskończoność. Wniosek: Achilles nigdy nie dogoni żółwia, mimo że biegnie od niego dwa razy szybciej, gdyż zawsze będzie dzieliła ich zmniejszająca się odległość.

Strzała

Załóżmy, że wystrzelona z łuku strzała pokonała określony dowolny odcinek drogi. Można więc powiedzieć, że w momencie wystrzelenia znajdowała się ona na początku tej trasy, a po dotarciu do celu – na końcu. Pytanie jednak, gdzie przebywała w trakcie pokonywania tej drogi. Można odpowiedzieć, że w 1/4 czasu pokonywania tego odcinka musiała być niewątpliwie w 1/4 odcinka. Gdy zadamy pytanie, gdzie była po 1/2 czasu lotu, znowu można odpowiedzieć, że w 1/2 odcinka. Po 3/4 czasu – w 3/4 odcinka, i tak dalej w nieskończoność. Możemy sobie wyobrażać dowolną chwilę lotu, w którym strzała znajdowała się w jakimś konkretnym punkcie, w konkretnej odległości od łucznika. Czyli możemy powiedzieć, że skoro w każdej chwili znajdowała się w jakimś konkretnym punkcie, więc w każdej chwili była w spoczynku. Niemożliwe jest zatem, aby w każdej chwili czasu strzała pozostawała w spoczynku i poruszała się jednocześnie.

Stadion

Rozważmy wyścig rydwanów. Szybkość, z jaką rydwany poruszają się, jest jednocześnie taka i inna, mniejsza i większa, w zależności od tego, względem jakich innych przedmiotów (rydwanów) jest rozważana. Jeśli zaś ruch dokonuje się z szybkością, która jest jednocześnie „taka i nie taka”, to jest sprzeczny i nie może istnieć.

Szkic poglądowy:

AAAA

BBBB→

←CCCC

Szereg rydwanów A stoi, szeregi B i C poruszają się różnymi torami z jednakową szybkością w przeciwne strony. Względna szybkość, z którą mijają się B i C, jest dwukrotnie większa od tej, z jaką każdy z nich mija A.

Dawne próby rozwiązania paradoksów

• Dowodzono, iż w świecie rzeczywistym nie można dzielić odcinków w nieskończoność, a także, że wszystkie zjawiska zachodzące w nim są ciągłe, a nie punktowe, jak w ujęciu Zenona.
• Matematyk Giovanni Benedetti (1530–1590) twierdził, iż „zatrzymywanie” obiektów w ich ruchu to dostrzeganie jedynie części zjawiska, bowiem między statycznymi obrazami znajdują się nieskończenie krótkie odcinki czasu, w których obiekt przebywa odpowiednie odcinki drogi.

Dzisiejsze rozwiązania

• W przypadku paradoksów dychotomii i Achillesa można w matematyczny sposób udowodnić, że suma nieskończonej liczby odcinków może dać odcinek o skończonej długości, a więc czas potrzebny do pokonania go również jest skończony.
• Paradoks stadionu natomiast nie dowodzi sprzeczności ruchu, ale jego względności.

Pozostałe paradoksy Zenona

1. Miara. Jeśli wielkość istnieje, musi być jednocześnie nieskończenie mała i nieskończenie duża. Wielkość z definicji musi być podzielna, podzielna zaś jest, dopóki jej części posiadają wielkość. Jeżeli jest nieskończenie podzielna, to składa się z nieskończenie wielu części. Jeżeli części te nie mają wielkości, to również całość, złożona z części pozbawionych wielkości, musiałaby być pozbawiona wielkości. Jeżeli części mają skończoną wielkość, to całość, jako złożona z nieskończenie wielu części posiadających jakąś wielkość, byłaby nieskończonej wielkości.

2. Ilość. Jeśli wielość istnieje, musi być zarówno skończona i nieskończona w ilości. Jeśli rzeczy jest tyle, ile jest, to ich ilość powinna być skończona. Jednak każde dwie rzeczy są oddzielone przez trzecią, a pomiędzy nimi są następne i tak dalej. I tak liczba istniejących rzeczy jest nieograniczona.

3. Miejsce. Jeżeli wszystko, co istnieje, zajmuje jakieś miejsce, to również miejsce musi mieć swoje miejsce i tak dalej, w nieskończoność.

4. Soryt od gr. σωρός, czyli stos: Jaką najmniejszą liczbę ziaren nazwać można stosem (ziaren)?

5. Siew. Skoro przy zasiewaniu pojedynczego ziarna brak jest wrażeń słuchowych, to przy zasiewaniu większej ilości szum musi być złudzeniem.

Argumenty przeciwko wielości opierają się na błędnym założeniu (tym samym co argumenty przeciw ruchowi), iż można dzielić w nieskończoność. Błędność „siewu” polega na wyciąganiu wniosku ze zbyt niskiego poziomu szumu przy sianiu małej ilości ziarna.

Linki zewnętrzne

• BradleyB. Dowden BradleyB., Zeno’s Paradoxes, Internet Encyclopedia of Philosophy, ISSN 2161-0002 [dostęp 2018-06-28]  (ang.).

Artykuły na Stanford Encyclopedia of Philosophy (ang.) [dostęp 2018-08-02]:

• NickN. Hugget NickN., Zeno’s paradoxes, 11 czerwca 2018 . (Paradoksy Zenona)
• JohnJ. Manchak JohnJ., Bryan W.B.W. Roberts Bryan W.B.W., Supertasks, 5 kwietnia 2016 . (Superczynności)
• Zenon z Elei – doksografia i fragmenty
• Paradoks dychotomii
• Apagogiczne argumenty Zenona z Elei w apologii Parmenidesa