Prędkość dryfu
Prędkość dryfu (prędkość unoszenia) – średnia prędkość jaką ma cząstka (elektron, dziura, jon itp.) w materiale, w którym płynie prąd elektryczny[1]. Używanie tego pojęcia w odniesieniu do cząstek w próżni nie ma sensu, gdyż są one przyspieszane a ich prędkość zależy od różnicy potencjałów, ich masy i miejsca. W przypadku zaś ośrodków materialnych (ciało stałe, ciecz, gaz itp.) ruch przyspieszanej cząstki jest spowalniany przez oddziaływania z siecią krystaliczną (w ciele stałym) lub inne cząstki (w cieczy, gazie). W układzie będącym w stanie równowagi prędkość cząstek podlegają pewnemu rozkładowi. Nawet gdy nie ma możliwości poznania go, można posługiwać się mierzalną wielkością makroskopową: średnią prędkością cząstki, czyli właśnie prędkością dryfu.
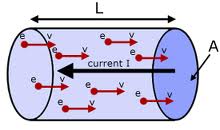
Prędkość dryfu elektronów w przewodniku o długości w którym płynie prąd stały, można określić na podstawie koncentracji elektronów przewodnictwa pola przekroju poprzecznego i natężenia prądu [1].
W objętości przewodnika jest elektronów przewodnictwa:
Ich sumaryczny ładunek wynosi zatem:
Natężenie prądu w przewodzie jest równe:
Prędkość dryfu to:
Stąd wynika:
Prędkość dryfu można także wyrazić przez gęstość prądu[1]:
Elektrony mają ładunek ujemny, więc wektory i mają przeciwne zwroty.
Podstawiając przykładowe dane, odpowiadające silnie obciążonemu przewodowi w instalacji elektrycznej:
Otrzymujemy:

















