Trójkąt Penrose’a

Trójkąt Penrose’a – figura niemożliwa wymyślona przez szwedzkiego grafika Oscara Reutersvärda w 1936 roku. Jej nazwa pochodzi od matematyka Rogera Penrose’a, który niezależnie odkrył i spopularyzował ją w latach 50. XX wieku, opisując jako „niemożliwość w najczystszej postaci”.
Opis[edytuj | edytuj kod]
Trójkąt Penrose’a objawia się jako przedmiot utworzony z trzech równych belek o kwadratowym przekroju, których końce są połączone, tworząc kąty proste, a cała figura ma kształt trójkątny. Belki mogą być od siebie oddzielone jako sześciany lub prostopadłościany i jedynie ułożone w kształt trójkąta Penrose’a.

Taki układ cech nie może być zrealizowany przez żaden trójwymiarowy obiekt w zwykłej przestrzeni euklidesowej. Taki obiekt może istnieć w pewnych 3-rozmaitościach euklidesowych[1]. Istnieją trójwymiarowe przedmioty, które obserwowane z odpowiedniej pozycji przedstawiają się jak dwuwymiarowy widok trójkąta Penrose’a. Termin „trójkąt Penrose’a” może oznaczać zarówno dwuwymiarowe odwzorowanie figury, jak i samą figurę niemożliwą.
Litografia holenderskiego grafika Mauritsa Cornelisa Eschera Wodospad[2] przedstawia wodę spływającą zygzakowatym kanałem umieszczonym na dwóch bokach trójkątów Penrose’a i kończącą bieg dwa piętra wyżej nad początkiem kanału. W efekcie końcowy wodospad tworzy trzeci bok obu trójkątów, napędzając ponadto koło wodne.
Jeśli dookoła trójkąta Penrose’a wykreśli się linię, utworzy ona trójpętlową wstęgę Möbiusa.
Inne wielokąty Penrose’a[edytuj | edytuj kod]
Mimo że jest możliwe tworzenie analogicznych figur na bazie innych wielokątów foremnych, efekt wizualny nie jest już tak uderzający. Wraz ze wzrostem liczby boków figury wydają się bardziej krzywe i poskręcane.
-
Kwadrat Penrose’a
-
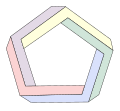
Pięciokąt Penrose’a
-
Sześciokąt Penrose’a
-
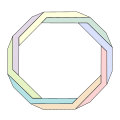
Ośmiokąt Penrose’a
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
Bibliografia[edytuj | edytuj kod]
- George Francis, A topological picturebook, Springer, 1988, ISBN 0-387-96426-6.
- Elżbieta Stróżecka, W magicznym zwierciadle Eschera [online], Wrocławski Portal Matematyczny, 20 grudnia 2012 [dostęp 2013-12-28].
Linki zewnętrzne[edytuj | edytuj kod]
- Litografia Waterfall w anglojęzycznej Wikipedii
- Zenon Kulpa, Figury niemożliwe, czyli ogólna teoria smoków [online], 2005 [dostęp 2023-03-08].
- ZenoTheRogue, Impossible Triangle Possible in Nil Geometry [online], YouTube, 12 lutego 2020 [dostęp 2020-07-22].