Drgania swobodne

Drgania swobodne – drgania ciała wywołane wychyleniem z położenia równowagi trwałej, kiedy na ciało nie działają żadne siły, poza siłami określającymi położenie równowagi i siłami dążącymi do jej przywrócenia[1].
Drgania swobodne obejmują szeroki zakres rodzajów drgań, w analizie drgań wyszczególnia się drgania układów w zależności od ich okresowości, liniowości, występowania rozpraszania energii (tłumienia), liczby stopni swobody układu. Liniowość układu zapewnia niezależność częstotliwości drgań od amplitudy (izochronizm).
Drgania o jednym stopniu swobody[edytuj | edytuj kod]
Najprostszym rodzajem drgań są drgania liniowego układu o jednym stopniu swobody bez tłumienia jego drgania są harmoniczne, a układ drgający zwany jest oscylatorem harmonicznym. Drgania swobodne układu o jednym stopniu swobody mogą być opisane równaniem[2]:
Jego rozwiązania można przedstawić w postaciach:
Amplituda i przesunięcie fazowe określone są przez warunki początkowe drgań:
gdzie:
- – częstość własna,
- – amplituda drgań,
- – wychylenie początkowe,
- – prędkość początkowa.
Częstość drgań nietłumionych nosi nazwę częstości własnej układu drgań i jest jego cechą charakterystyczną.
Przykład drgań swobodnych[edytuj | edytuj kod]
Drgania swobodne wykonują ciała sprężyste, jeżeli amplituda drgań nie jest zbyt duża. Dla małych drgań jest spełnione prawo Hooke’a, mówiące o proporcjonalności siły do wielkości odkształcenia.
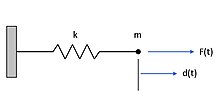
Częstotliwość drgań własnych zależy tylko od własności fizycznych i kształtu ciała, lub układu drgającego, jeżeli drgania wykonywane są pod wpływem wewnętrznych sił sprężystości ciała. Przykładem może być ciało o masie wykonujące poziome drgania spowodowane oddziaływaniem sprężyny o współczynniku sprężystości Równanie ruchu i jego rozwiązanie:
Ciało wykonuje drgania swobodne o określonej częstości bez względu na sposób pobudzenia oraz siłę pobudzenia.


Drgania układów o wielu stopniach swobody[edytuj | edytuj kod]
Liniowe i nietłumione układy o wielu stopniach swobody, np. kilka ciał połączonych sprężynami, mogą wykonywać drgania w różnej postaci. Drgania te można przedstawić jako sumę drgań harmonicznych zwanych drganiami własnymi lub drganiami normalnymi[1]. Drgania kolejnych stopni swobody są sumą drgań harmonicznych, co można wyrazić wzorem[2]:
gdzie:
- – uogólniona współrzędna opisująca drgania stopnia swobody
- – amplituda odpowiedniego składnika drgań,
- – częstość harmonicznej
Jeżeli współrzędne opisujące drgania dobrano tak, że każdy składnik jest niezależny od pozostałych, to ten układ współrzędnych nazywa się współrzędnymi normalnymi, a składowe drgań drganiami normalnymi.
Liczba drgań normalnych układu jest równa liczbie stopni swobody.
Przykład[edytuj | edytuj kod]
jednakowych mas o numerach połączonych identycznymi sprężynami, drgającymi tylko wzdłuż osi układu ma stopni swobody. Kolejna masa tego układu drgającego, będąca jego kolejnym stopniem swobody, wykonuje drgania w postaci:
Dla danego drgania normalnego wszystkie masy wykonują drgania o tej samej częstości, zależnej od stanu układu i tym samym przesunięciu fazowym zależnym od warunków początkowych, amplitudy drgań są zależne od warunków początkowych, oraz warunków układu (wartość funkcji sinus). Układ może drgać z największą częstością gdy Kolejne częstości nie są wielokrotnością najmniejszej częstości ale jeżeli to kolejne drgania własne są wielokrotnościami częstości podstawowej (są harmonicznymi).
Częstotliwości poszczególnych drgań własnych w przybliżeniu liniowym nie zależą od sposobu wzbudzania i dostarczonej energii, ale od sposobu wzbudzenia zależą zależności między amplitudami poszczególnych drgań normalnych. Na przykład uderzając w dzwon w różnych miejscach, z różną siłą, różnymi przedmiotami – spowodujemy, że będziemy słyszeli różnie brzmiące dźwięki – o różnej barwie. Oznacza to, że za każdym razem dzwon wykonuje nieco inne drgania. Drgania te będą różniły się składem widmowym, ale będą zawsze sumą drgań o takich samych częstotliwościach.
Jeżeli w powyższym przykładzie odległości między kolejnymi masami wynoszą to:
- – długość układu,
- – położenie równowagi kolejnej masy.
Drgania masy można wyrazić:
gdzie:
- – liczba falowa, opisuje zależność drgań od miejsca układu,
Ostatni zapis drgań jest równoważny równaniu fali stojącej, oznacza to że drganie normalne jest falą stojącą w układzie. Częstość drgań można wyrazić jako zależność od liczby falowej, związek ten jest nazywany dyspersją fali. W tym przykładzie związek ten określa zależność:
Układ wielu drgających ciał jest używany w fizyce do modelowania drgań atomów w sieci krystalicznej[3] drgań atomów i zrębów atomowych w cząsteczkach. Przykładem modelu opartego na drganiach atomów sieci krystalicznej jest model Debye’a ciała stałego.
Drgania swobodne w ośrodkach ciągłych[edytuj | edytuj kod]
Sprężyste ośrodki ciągłe mogą być modelowane przez zastąpienie ośrodka ciągłego układem oddziałujących punktowych mas. Traktując jednowymiarowy ciąg drgających mas jako elementy ciągłej struny, drania swobodne odpowiadają fali stojącej struny. Fala stojąca jest sumą drgań własnych ośrodka. Ośrodek ciągły składa się z nieskończenie wielu drgających elementów, mają one nieskończenie wiele drgań własnych.
Drgania swobodne tłumione[edytuj | edytuj kod]
Tłumienie drgań swobodnych powoduje zmniejszanie energii układu drgań, co obserwuje się jako zmniejszanie amplitudy drgań. Siłę oporu można uwzględnić w równaniu drgań, wprowadzając składnik proporcjonalny do szybkości zmian wielkości drgającej:
Warunkami początkowymi rozwiązania równania jest położenie początkowe i prędkość początkowa będąca pochodną położenia:
Rozwiązaniem równania, po uwzględnieniu warunków początkowych, mogą być zależności postaci:
Współczynnik tłumienia zwany stałą zaniku drgań jest odwrotnością średniego czasu drgań.
Wzór składa się z 3 czynników. Pierwszy określa amplitudę drgań, drugi odpowiada za zmniejszanie się drgań, trzeci stanowi część oscylacyjną. Wprowadzenie oporów do układu zmniejsza jego częstość drgań przy silnym tłumieniu ( drgania nie występują).
Gdy tłumienie jest słabe drgania są określane jako słabo tłumione, czynnik określający zmniejszanie drgań niewiele zmienia się w czasie jednego okresu drgań. Takie drgania określa się jako prawie okresowe.
W drganiach tłumionych układu o wielu stopniach swobody każdy rodzaj drgań może być tłumiony z innym natężeniem, dlatego układy takie rozpatruje się jako sumę drgań harmonicznych tłumionych dla każdej częstotliwości[2].
















































