Papier, kamień, nożyce

Ten artykuł od 2024-05 zawiera treści, przy których brakuje odnośników do źródeł.

Należy dodać przypisy do treści niemających odnośników do źródeł. Dodanie listy źródeł bibliograficznych jest problematyczne, ponieważ nie wiadomo, które treści one uźródławiają.
Sprawdź w źródłach: Encyklopedia PWN • Google Books • Google Scholar • Federacja Bibliotek Cyfrowych • BazHum • BazTech • RCIN • Internet Archive (texts / inlibrary)
Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu.
Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

Papier, kamień, nożyce (^{[potrzebny przypis]}) – gra towarzyska dla dwóch lub więcej osób, będąca uproszczoną wersją mory. W „papier, kamień, nożyce” gra się, używając dłoni graczy.

Zasady

Gra składa się z kolejnych tur. W każdej turze obydwaj gracze, na umówiony sygnał, szybko wystawiają przed siebie dłoń, pokazującą symbol papieru, kamienia lub nożyc. Gracz, który pokazał silniejszy symbol, otrzymuje jeden punkt. W przypadku pokazania dwóch takich samych symboli następuje remis – punktu brak. Oto hierarchia symboli:

nożyce są silniejsze od papieru, ponieważ go tną,
kamień jest silniejszy od nożyc, ponieważ je tępi lub łamie,
papier jest silniejszy od kamienia, ponieważ go owija.

Gracz, który pierwszy uzyska umówioną wcześniej liczbę punktów, wygrywa partię.

Papier, kamień, nożyce
papier owija kamień
kamień tępi nożyce
nożyce tną papier

Formalna analiza

Formalnie, papier, kamień, nożyce można rozważać jako grę o sumie zerowej. Przykładowe wyniki w grze przedstawia poniższa tabela, gdzie (1,-1) oznacza zwycięstwo gracza A i przegraną gracza B (–1,1) oznacza zwycięstwo gracza B i przegraną gracza A, a (0,0) oznacza remis.

Gracz A / Gracz B	Papier	Kamień	Nożyce
Papier	(0,0)	(1,–1)	(–1,1)
Kamień	(–1,1)	(0,0)	(1,–1)
Nożyce	(1,–1)	(–1,1)	(0,0)

Gra w papier, kamień, nożyce nie posiada równowagi Nasha w strategiach czystych. Znając deterministyczną strategię przeciwnika i grając optymalnie, każdy z graczy może zapewnić sobie zwycięstwo.

Gra w papier, kamień, nożyce posiada jednak równowagę Nasha w strategiach mieszanych. Ma to miejsce wówczas, gdy każdy z graczy randomizuje, wybierając każdą z dostępnych mu opcji z jednakowym prawdopodobieństwem 1/3.

Historia

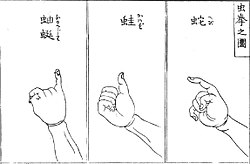
Gra została wynaleziona w Japonii pod koniec XIX w. pod nazwą Jan-ken-pon (jap. じゃんけんぽん) lub bardziej potoczną nazwą janken (jap. じゃんけん) i rozpowszechniona po świecie w XX w. Pochodzenie nazwy nie jest znane.

Papier, kamień, nożyce, jaszczurka, Spock

Odmiana gry, która poza standardowymi trzema gestami występuje jaszczurka (palce złożone w symbol przypominające jaszczurczy pysk) oraz Spock formowany przez charakterystyczny salut wolkański z filmów serii Star Trek (mały i serdeczny palec oddzielone od środkowego i wskazującego). Gra została wymyślona przez Sama Kassa i Kerena Bryla^[1]. Spopularyzowana^[2] została przez serial Teoria wielkiego podrywu – zwłaszcza odcinek ósmy sezonu drugiego: The Lizard-Spock Expansion, który jest grze poświęcony^[3]. Sheldon Cooper gra w nią z doktorem Koothrappalim, stale remisując na figurze Spocka. Gra lub jej reguły pojawiają się także w odcinku 20. tego sezonu, oraz w odcinku 17. sezonu piątego^[4].

Zasady

Gracze na umówiony sygnał wyciągają przed siebie dłonie, pokazując jeden z pięciu symboli. Wygrywa ten, który pokazał silniejszy. W przypadku pokazania tych samych symboli następuje remis. Między symbolami zachodzą następujące relacje^[1]^[5]:

kamień tępi nożyce,
nożyce tną papier,
papier zakrywa kamień,
kamień zgniata jaszczurkę,
jaszczurka truje Spocka,
Spock niszczy nożyce,
nożyce dekapitują jaszczurkę,
jaszczurka zjada papier,
papier obala Spocka,
Spock dezintegruje kamień.

Symbole tworzą dziesięć par. Każdy z symboli występuje w czterech parach, przy czym wygrywa w dwóch i przegrywa w pozostałych dwóch^[6].

Przypisy

↑ ^a ^b Rock Paper Scissors Spock Lizard. samkass.com. [dostęp 2015-11-06]. (ang.).
↑ John Hickman: Rock, paper, scissors, lizard, Spock… and global warming policy choice. thespacereview.com. [dostęp 2016-05-26]. (ang.).
↑ The Lizard-Spock Expansion w bazie IMDb (ang.)
↑ Rock-paper-scissors-lizard-Spock. [dostęp 2016-05-26].
↑ The Lizard-Spock Expansion. Quotes. IMDb. [dostęp 2016-05-26]. (ang.).
↑ How to Play Rock Paper Scissors Lizard Spock. wikihow.com. [dostęp 2016-05-26]. (ang.).

Bibliografia

Tę sekcję należy dopracować:

należy ustalić, do których fragmentów odnosi się bibliografia (należy wstawić odpowiednie przypisy).
Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tej sekcji.
Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tej sekcji.

LechL. Pijanowski LechL., Skarbnica gier, Warszawa: Młodzieżowa Agencja Wydawnicza, 1981, ISBN 83-203-0092-4, OCLC 830205881 .

[RPSSL-1] Rock Paper Scissors Spock Lizard. samkass.com. [dostęp 2015-11-06]. (ang.).

[2] John Hickman: Rock, paper, scissors, lizard, Spock… and global warming policy choice. thespacereview.com. [dostęp 2016-05-26]. (ang.).

[3] The Lizard-Spock Expansion w bazie IMDb (ang.)

[4] Rock-paper-scissors-lizard-Spock. [dostęp 2016-05-26].

[5] The Lizard-Spock Expansion. Quotes. IMDb. [dostęp 2016-05-26]. (ang.).

[6] How to Play Rock Paper Scissors Lizard Spock. wikihow.com. [dostęp 2016-05-26]. (ang.).

[1]

[2]

[3]

[4]

[5]

[6]