Szereg 1 + 1 + 1 + 1 + …

Asymptotyczna charakterystyka szeregu rozbieżnego 1 + 1 + 1 + 1 + ⋯.

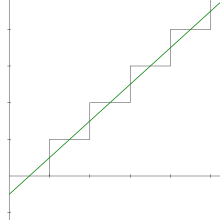
Szereg 1 + 1 + 1 + 1 + … – szereg rozbieżny, czyli niemający skończonej sumy według podstawowej definicji. Jego sumy cząstkowe rosną do nieskończoności. Można go zapisywać również jako $\sum _{n=1}^{\infty }n^{0}.$

Jeśli taki szereg pojawia się podczas analizy zjawisk fizycznych, może on być czasami interpretowany przez zastosowanie regularyzacji funkcją dzeta, tj. w tym przypadku określenie wartości funkcji dzeta Riemanna w punkcie $s=0$

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1-2^{1-s}}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}.$

Oba wyrażenia podane wyżej nie są „wyliczalne” dla wartości zero, dlatego też stosuje się przedłużenie analityczne funkcji dzeta Riemanna

$\zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s).$

Dzięki niemu (wiedząc, że $\Gamma (1)=1$) otrzymujemy:

$\zeta (0)={\frac {1}{\pi }}\lim _{s\to 0}\ \sin \left({\frac {\pi s}{2}}\right)\ \zeta (1-s)={\frac {1}{\pi }}\lim _{s\to 0}\ \left({\frac {\pi s}{2}}-{\frac {\pi ^{3}s^{3}}{48}}+\dots \right)\ \left(-{\frac {1}{s}}+\dots \right)=-{\frac {1}{2}},$

gdzie rozwinięcie w szereg potęgowy $\zeta (s)$ w otoczeniu $s=1$ zachodzi, ponieważ $\zeta (s)$ ma w nim pojedynczy biegun z residuum równym 1. W tym sensie $1+1+1+1+\dots =\zeta (0)=-{\tfrac {1}{2}}$.

Zobacz też

• szereg Grandiego
• szereg 1 + 2 + 3 + 4 + …
• szereg 1 + 2 + 4 + 8 + …