Koło zębate

Przykłady kół zębatych o zębach prostych i śrubowych

Koło zębate – element czynny przekładni zębatej oraz element innych mechanizmów takich jak sprzęgło zębate, pompa zębata i innych.

W skład koła zębatego wchodzą:

• wieniec zębaty
• piasta
• łącznik (łączący piastę i wieniec).

W niektórych kołach zębatych, szczególnie tych o niewielkiej liczbie zębów i małej średnicy, nie występuje łącznik, a wieniec zębaty spełnia jednocześnie rolę piasty. Takiego rodzaju koło zębate nazywa się zębnikiem. Zębnik często nacięty jest bezpośrednio na wale i tworzy z nim integralną całość lub osadzony jest na nim za pomocą połączenia wciskowego.

Wieniec zębaty składa się z zębów i wieńca, z którego zęby wystają. Przestrzenie pomiędzy zębami nazywane są wrębami.

Parametry koła zębatego

Parametry koła zębatego i zębów

Ząb koła zębatego

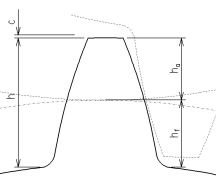
$z$ – liczba zębów

$d$ – średnica podziałowa

średnica okręgu, na którym szerokość wrębu jest równa grubości zęba

$d_{a}$ – średnica wierzchołkowa

średnica okręgu przechodzącego przez wierzchołki zębów

$d_{f}$ – średnica stóp

średnica okręgu przechodzącego przez dna wrębów

$d_{b}$ – średnica koła zasadniczego

średnica wyobrażalnego koła, z którego rozwijane są zarysy ewolwentowe boków zębów

$p$ – podziałka obwodowa

odległość jednoimiennych boków zębów mierzona na łuku koła podziałowego

$p_{b}$ – podziałka zasadnicza

podziałka mierzona wzdłuż łuku koła zasadniczego

$m$ – moduł zęba

parametr charakteryzujący wielkość zębów koła zębatego. Moduły kół współpracujących muszą być takie same. Moduł zęba jest wielkością znormalizowaną przez Polską Normę PN/M-88502. Oblicza się go ze wzoru $m=p\div \Pi$

$h$ – wysokość zęba

suma wysokości głowy i stopy zęba

$h_{a}$ – wysokość głowy zęba

$h_{f}$ – wysokość stopy zęba

$y$ – współczynnik wysokości zęba

wysokość głowy zęba wyrażona w krotności modułu

$y=1$ zęby normalne stosowane w większości przekładni zębatych

$y<1$ zęby niskie stosuje się w przekładniach zębatych stożkowych o zębach łukowych, w których koło małe ma niewielką liczbę zębów (od 5 do 10), w przekładniach ślimakowych, w sprzęgłach zębatych, w ewolwentowych połączeniach wielowypustowych

$y>1$ zęby wysokie stosowane w pompach zębatych.

$x$ – współczynnik korekcji

przesunięcie zarysu odniesienia przy wykonywaniu koła zębatego wyrażone w krotności modułu

$x=0$ koło niekorygowane

$x>0$ odsunięcie zarysu odniesienia np. dla uniknięcia podcinania zębów

$x<0$ dosunięcie zarysu odniesienia

$c$ – luz wierzchołkowy

zwykle 0,2–0,25 modułu

Kształt linii zęba

• zęby proste
• zęby śrubowe
• zęby daszkowe (w przekładniach walcowych)
• zęby krzywoliniowe (w przekładniach stożkowych)

Mechanika zazębienia

Schemat mechaniki zazębienia

Animacja zazębienia

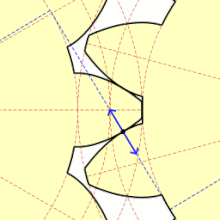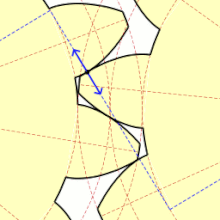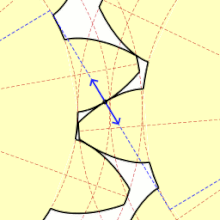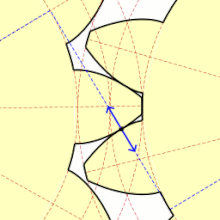
Podczas obrotu kół dwa współpracujące zęby otaczają się jednocześnie także, ślizgając się po sobie. Ten poślizg jest niekorzystnym, lecz niemożliwym do uniknięcia zjawiskiem. Tylko w bardzo wąskim zakresie, który teoretycznie sprowadza się do jednego punktu $C,$ występuje czyste toczenie się zębów bez poślizgu. Punkt ten nazywa się punktem tocznym, który wyznacza koło toczne o średnicy $d_{w}.$ Koła toczne dla obu współpracujących kół są styczne w punkcie $C.$

Punkty styku zębów w czasie obrotu układają się na odcinku ($E_{1},$ $E_{2}$) zwanym odcinkiem przyporu. Kąt $\alpha$ zawarty między tym odcinkiem a linią styczną do kół tocznych w punkcie tocznym jest zwany kątem przyporu i jest jednocześnie parametrem ewolwenty. Zarys nominalny, powszechnie używany w budowie maszyn i przyjęty przez praktycznie wszystkie normy na całym świecie ma kąt przyporu $\alpha =20^{\circ }$ Jednocześnie dla zarysu nominalnego średnice podziałowe kół pokrywają się z kołami tocznymi.

Obliczenia wytrzymałościowe

Ze względu na złożoność zjawisk zachodzących w uzębieniu niemożliwe jest stworzenie analitycznej metody obliczania wytrzymałości zęba. Tradycyjnie stosowane są tu metody parametryczne, które pozwalają uwzględnić szereg parametrów pracy przekładni takich jak – przenoszona moc, prędkość kół, wielkość, przełożenia, liczba zębów, intensywność pracy, rodzaj smarowania oraz chłodzenia itp. parametry związane są empirycznymi formułami i w ostateczności pozwalają na obliczenie minimalnego wymaganego modułu zęba.

Współczesna technologia dostarcza komputerowych metod modelowania zjawisk wewnątrz obciążonych części maszyn, także i kół zębatych, co znacznie ułatwia przeprowadzenie ewaluacji konstrukcji.

Szczególnym przypadkiem kół zębatych są:

• koła w kształcie owalu albo serca stosowane w przekładniach o przełożeniu zmiennym w czasie każdego obrotu, które mimo odmiennego kształtu są nazywane kołami zębatymi
• koła przekładni łańcuchowej o zmiennym przełożeniu składające się z ruchomych segmentów
• wycinek koła stosowany w przekładniach o niepełnym obrocie np. w mechanizmie podniesienia działa.

Obliczenia wytrzymałościowe dla koła zębatego walcowego prostego:

1. Obliczenie modułu z warunku na zginanie
2. Obliczenie modułu z warunku na naciski powierzchniowe
3. Dobór modułu według tablicy
4. Obliczenie pozostałych parametrów koła zębatego

Obliczenia

0. Zaczynamy od określenia danych wstępnych: $n_{1},z_{1},u,M{:}$

$u$ – przełożenie,

$M_{o}={\tfrac {M\cdot K_{p}\cdot K_{v}}{K_{e}}},$

gdzie:

$K_{v}=1{,}25{\text{–}}2{,}3$ (współczynnik nadwyżek dynamicznych, zależy od prędkości obwodowej koła),

$K_{e}=1$ lub $K_{e}=2$ (współczynnik zależny od liczby przyporu),

$K_{p}=1{\text{–}}2$ (współczynnik przeciążenia zależny od warunków pracy).

1. Moduł z warunku na zginanie:

$m\geqslant {\sqrt[{3}]{\tfrac {2M_{o}\cdot q}{\lambda \cdot z_{1}\cdot k_{gj}}}},$

$v=100\cdot {\tfrac {\pi \cdot d_{1}\cdot n}{60}},$

$d_{1}=z_{1}\cdot m$ – średnica podziałowa,

$b=\lambda \cdot m$ – szerokość wieńca,

gdzie:

$q,$ $\lambda ,$ $k_{gj}$ – z tablic.

2. Obliczanie zębów na naciski powierzchniowe:

$p_{max}={\sqrt {2/(1/E_{1}+1/E_{2})\cdot \Pi \cdot \sin \alpha \cdot \cos \alpha }}\cdot {\sqrt {F/(b\cdot d)\cdot 1\pm 1/i}},$

gdzie:

$E_{1},$ $E_{2}$ – moduły Younga materiałów uzębień w MPa,

$\alpha$ – kąt przyporu,

$F$ – siła nacisku kół na siebie,

$b$ – tzw. czynna szerokość uzębienia (grubość koła) w mm,

$i$ – przełożenie.

Obróbka uzębień

Frezowanie obwiedniowe frezem ślimakowym

Występuje wiele metod kształtowania uzębień kół zębatych wykonanych z metalu:

• kształtowe
  • frezowanie frezem modułowym krążkowym
  • frezowanie frezem palcowym
  • dłutowanie
  • struganie
  • przeciąganie
  • wycinanie elektroerozyjne (obróbka elektroerozyjna – WEDM)
• kopiowe
  • struganie według kopiału
• obwiedniowe
  • dłutowanie metodą Maaga
  • dłutowanie metodą Fellowsa
  • struganie metodą Sunderlanda
  • frezowanie obwiedniowe frezem ślimakowym walcowym lub globoidalnym
  • frezowanie frezem ślimakowym stożkowym
  • frezowanie głowicą frezową z zębami ustawionymi według okręgu
  • frezowanie głowicą frezową z zębami ustawionymi według spirali (spiral) Archimedesa

Koła zębate z tworzyw sztucznych wykonywane są głównie metodą wtryskiwania.

Zobacz też

• przednie zębatki rowerowe
• tylne koła zębate roweru