Charakterystyka Bodego

Charakterystyka Bodego – w teorii sterowania jedna z najważniejszych charakterystyk częstotliwościowych układu regulacji (lub jego członu, elementu).

Wyznacza się ją dla układu opisanego transmitancją widmową.

Charakterystyka ta obrazuje logarytmiczną zależność amplitudy i fazy od częstotliwości. Składa się z dwóch wykresów: charakterystyki amplitudowej oraz charakterystyki fazowej. Osie ω i A(ω) skaluje się logarytmicznie, wprowadzając tzw. moduł logarytmiczny Lm(ω)=20 lgA(ω), którego jednostką jest decybel (dB), wzmocnieniu 10-krotnemu odpowiada 20 dB, wzmocnieniu jednostkowemu 0 dB. Dla charakterystyki fazowej oś ω skaluje się logarytmicznie, oś ϕ(ω) pozostaje liniowa. Sposób przedstawienia w postaci częstotliwościowych charakterystyk logarytmicznych czyli w postaci wykresów Bodego stosuje się bardzo często (charakterystyki A(ω) i ϕ(ω) w skali liniowej są rzadko stosowane).

Nazwa charakterystyka Bodego pochodzi od nazwiska amerykańskiego naukowca holenderskiego pochodzenia – Henrika Wade'a Bodego.

Charakterystyki Bodego podstawowych elementów [edytuj]

W poniższej tabeli górny wykres przedstawia logarytmiczną charakterystykę amplitudową, a dolny logarytmiczną charakterystykę fazową. Amplitudę wyrażono w decybelach, fazę w stopniach, a częstość ( $\omega \,$ ) w radianach na sekundę.

Częstość jest liniowo zależna od częstotliwości: $\omega \, = 2 \;\pi\;f$ .

Nr	Nazwa	Transmitancja operatorowa	Uwagi
1	Element proporcjonalny	$\ K$	$\ K = 100$
2	Element całkujący	$\frac{1}{s}$
3	Element różniczkujący	$\ s$
4	Element inercyjny pierwszego rzędu	$\frac{1}{Ts+1}$	$\ T = 0,01$
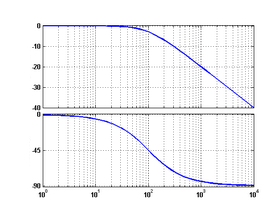5	Element oscylacyjny	$\frac{1}{T^2s^2 + 2\;\xi\ T s + 1}$	$\ T = 0,01$ $\xi\ = 0,1$
6	Element opóźniający	$\ e^{-sT}$	$\ T = 0,0001$