Radian

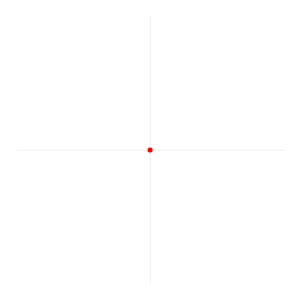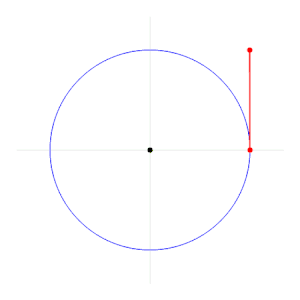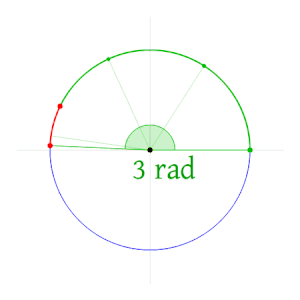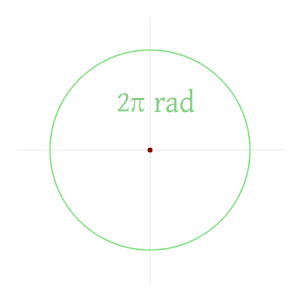
Radian (w skrócie rad od łac. radius „promień”) – jednostka miary łukowej kąta płaskiego zdefiniowana jako miara kąta środkowego, w którym długość łuku wyznaczonego przez kąt środkowy jest równa promieniowi okręgu^[1]. Niemianowana jednostka pochodna układu SI.

Związek z innymi jednostkami[edytuj | edytuj kod]

Zachodzą następujące wzory zamiany miary łukowej kąta z jednostki:

stopniowej na radialną
$\alpha (\mathrm {rad} )={\frac {\alpha (^{\circ })\cdot \pi }{180^{\circ }}}\ \mathrm {rad} ,$
gradowej na radialną
$\alpha (\mathrm {rad} )={\frac {\alpha (^{\mathrm {g} })\cdot \pi }{200^{\mathrm {g} }}}\ \mathrm {rad} ,$

w związku z czym:

1\ \mathrm {rad} ={\frac {180^{\circ }}{\pi }}\approx 57{,}29577951^{\circ },

oraz

1\ \mathrm {rad} ={\frac {200^{\mathrm {g} }}{\pi }}\approx 63{,}66197724^{\mathrm {g} }.

Kąt o mierze łukowej 36° (podanej w stopniach) ma miarę wyrażoną w radianach równą

36^{\circ }\cdot {\frac {\pi }{180^{\circ }}}\approx 0{,}628\ \mathrm {rad} .

α (°)	α [rad]	sin α	tg α
40	0,698132	0,642788	0,839100
30	0,523599	0,500000	0,577350
20	0,349066	0,342020	0,363970
10	0,174533	0,173648	0,176327
5	0,087266	0,087156	0,087489
2	0,034907	0,034899	0,034921
1	0,017453	0,017452	0,017455