Epicykloida

Epicykloida – krzywa, jaką zakreśla ustalony punkt okręgu toczącego się bez poślizgu na zewnątrz innego, nieruchomego okręgu. Epicykloida jest szczególnym przypadkiem epitrochoidy.

Kształt epicykloidy zależy od stosunku ${\tfrac {R}{r}}$ promieni okręgów, nieruchomego do toczącego się. Gdy promienie są równe otrzymuje się krzywą sercową, z grecka zwaną kardioidą (sercowata od gr. καρδιά – serce).

Opis matematyczny

Epicykloidę najłatwiej opisać równaniami parametrycznymi:

$x=(R+r)\cos(t)-r\cos \left({\frac {R+r}{r}}t\right),$

$y=(R+r)\sin(t)-r\sin \left({\frac {R+r}{r}}t\right).$

Przykłady

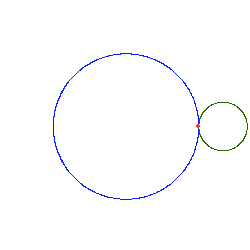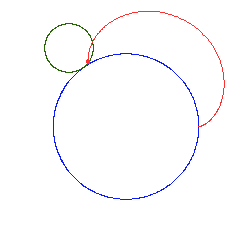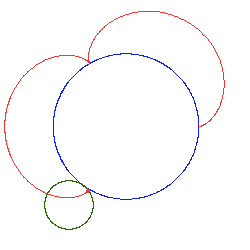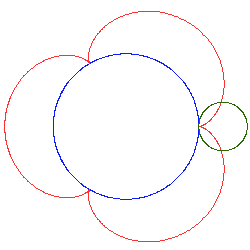
Poniższe rysunki pokazują kilka epicykloid dla różnych wartości ilorazów ${\tfrac {R}{r}}.$

• powstawanie kardioidy i kardioida statycznie:

• epicykloida ${\tfrac {R}{r}}=2$ (zwana też nefroidą) – powstawanie i krzywa statycznie:

• epicykloida ${\frac {R}{r}}=3$ – powstawanie i krzywa statycznie:

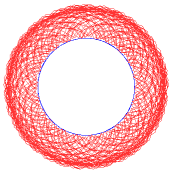
Jeżeli stosunek ${\frac {R}{r}}$ jest liczbą niewymierną, otrzymuje się krzywą otwartą. Kolejne przybliżenia takiej sytuacji pokazują poniższe rysunki:

Zobacz też

• cykloida
• epicentrum
• hipocykloida

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Epicycloid, [w:] MathWorld, Wolfram Research [dostęp 2020-12-13]  (ang.).