Orbita geostacjonarna
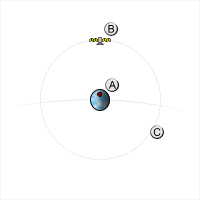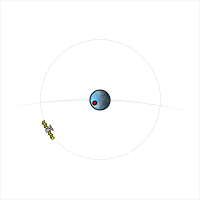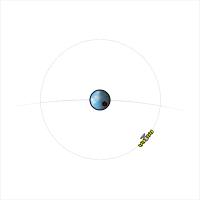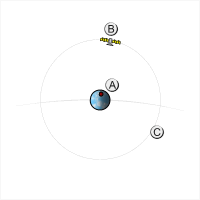
Orbita geostacjonarna – orbita okołoziemska, która zapewnia krążącemu po niej satelicie zachowanie stałej pozycji nad wybranym punktem równika Ziemi. Orbita geostacjonarna jest orbitą kołową, zawartą w płaszczyźnie równika. Przebiega na wysokości 35 786 km nad równikiem (42 160 km od środka Ziemi). Prędkość ciała na orbicie geostacjonarnej wynosi około 3,08 km/s, a czas okrążenia przez niego Ziemi jest równy 23 godziny 56 minut i 4 sekundy, czyli dokładnie tyle, ile trwa doba gwiazdowa.
Orbita geostacjonarna jest szczególnym przypadkiem orbity geosynchronicznej.
Historia[edytuj | edytuj kod]
Rozważania na temat satelitów geostacjonarnych przeznaczonych do celów komunikacyjnych po raz pierwszy opublikował w 1928 roku Herman Potočnik, jednak jego praca nie była zbyt szeroko znana[1]. Pierwsza wzmianka o orbicie geostacjonarnej w literaturze popularnej miała miejsce w opowiadaniu George’a O. Smitha pt. Venus Equilateral[2], jednak bez szczegółowej analizy zagadnienia. Dopiero brytyjski pisarz science-fiction Arthur C. Clarke upowszechnił szerzej tę ideę i dokonał szerszej analizy tematu w 1945 roku w magazynie „Wireless World” (obecnie „Electronics World”), w artykule Extra-Terrestrial Relays – Can Rocket Stations Give Worldwide Radio Coverage?[3], wywołując burzliwą dyskusję w kołach naukowych. Dlatego orbita geostacjonarna bywa nazywana orbitą Clarke’a[4].
Telekomunikacja[edytuj | edytuj kod]

Orbita geostacjonarna wykorzystywana jest przez satelity geostacjonarne, zwłaszcza telekomunikacyjne, meteorologiczne i telefonii satelitarnej. Także satelity SBAS wspomagające system GPS znajdują się na tej orbicie. Umieszczenie satelity na orbicie geostacjonarnej pozwala na utrzymanie stałej łączności z nim przy użyciu anteny kierunkowej, bez konieczności nieustannej zmiany kierunku ustawienia anteny. Wadą tego rozwiązania jest niemożliwość objęcia zasięgiem terenów okołobiegunowych, gdyż dla obserwatora znajdującego się na powierzchni Ziemi na północ od równoleżnika 81,3°N (oraz analogicznie na południe od równoleżnika 81,3°S) orbita geostacjonarna znajduje się w całości poniżej horyzontu. Graniczną szerokość geograficzną obliczono przy założeniu kulistości Ziemi ze wzoru:
Inną wadą orbity geostacjonarnej jest jej duża odległość od Ziemi w porównaniu z orbitami typu LEO lub MEO. W wyniku tego, minimalny czas pomiędzy wysłaniem sygnału radiowego z powierzchni Ziemi, jego przetworzeniem przez satelitę geostacjonarnego i ostatecznie odebraniem na powierzchni Ziemi w przybliżeniu jest równy 239 ms. Dla porównania, w przypadku satelitów systemu Iridium, znajdujących się na orbitach typu LEO 780 km nad powierzchnią Ziemi, czas ten jest równy około 5 ms. W praktyce opóźnienia te mogą być nawet kilkukrotnie większe, co odczuwalne jest szczególnie w przypadku prowadzenia satelitarnego połączenia telefonicznego.
Wyprowadzenie promienia orbity geostacjonarnej[edytuj | edytuj kod]


Kliknij obrazek, aby powiększyć i zobaczyć animację.
Na kołowej orbicie siła działająca na ciało jest siłą dośrodkową – w tym przypadku siłą tą jest siła przyciągania grawitacyjnego przyciągająca satelitę w kierunku środka Ziemi. Na orbicie geostacjonarnej czas obiegu Ziemi przez satelitę jest równy czasowi obrotu Ziemi wokół własnej osi, czyli dokładnie 1 dobie gwiazdowej.
Jak wspomniano wyżej, w ruchu satelity po orbicie kołowej siła grawitacji jest siłą dośrodkową
Z drugiej zasady dynamiki Newtona, dla satelity o masie wynika:
gdzie:
- – prędkość kątowa w radianach na sekundę,
- – promień orbity w metrach równy odległości do środka Ziemi.
Wartość przyspieszenia grawitacyjnego określa wzór:
gdzie:
- – masa Ziemi w kilogramach,
- – stała grawitacji.
Wartości obu przyspieszeń są równe:
Iloczyn zależny tylko od masy planety, zwany jest współczynnikiem grawitacyjnym ciała, dla Ziemi jest on równy
Ziemia wykonuje jeden obrót w czasie doby gwiazdowej, więc jej prędkość kątowa wynosi:
Z danych tych wynika, że promień orbity geostacjonarnej jest równy 42 164 km, co po odjęciu średniego promienia Ziemi równego 6378 km daje wysokość orbity (odległość od powierzchni Ziemi), równą 35 786 km.
Prędkość satelity na orbicie geostacjonarnej wynosi:
Wyprowadzenie granicznej szerokości geograficznej[edytuj | edytuj kod]
Z funkcji trygonometrycznych dla trójkąta prostokątnego otrzymamy:
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ Hermann Noordung: The Problem With Space Travel. DIANE Publishing, 1995, s. 72. ISBN 978-0-7881-1849-4. (angielskie tłumaczenie z języka niemieckiego).
- ↑ Cytat: (Korvus’s message is sent) to a small, squat building at the outskirts of Northern Landing. It was hurled at the sky. …It …arrived at the relay station tired and worn, …when it reached a space station only five hundred miles above the city of North Landing. George O. Smith: The Complete Venus Equilateral. New York: Ballantine Books, 1976, s. 3–4. ISBN 978-0-345-28953-7. (ang.).
- ↑ Arthur C. Clarke: Extra-Terrestrial Relays – Can Rocket Stations Give Worldwide Radio Coverage?. październik 1945. [dostęp 2015-08-15]. [zarchiwizowane z tego adresu (18 marca 2009)]. (ang.).
- ↑ Basics of Space Flight Section 1 Part 5, Geostationary Orbits. NASA. (ang.).















![{\displaystyle r={\sqrt[{3}]{\frac {G\cdot M}{\omega ^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75bfdbddd5fcb01e65560c672f33d2e21ef0271c)








