Kodowanie Huffmana
 Przykładowe działanie kodowania Huffmana |
Kodowanie Huffmana (ang. Huffman coding) – jedna z najprostszych i łatwych w implementacji metod kompresji bezstratnej[1]. Została opracowana w 1952 roku przez Amerykanina Davida Huffmana[2].
Algorytm Huffmana nie należy do najefektywniejszych obliczeniowo systemów bezstratnej kompresji danych, dlatego też praktycznie nie używa się go samodzielnie. Często wykorzystuje się go jako ostatni etap w różnych systemach kompresji, zarówno bezstratnej, jak i stratnej, np. MP3 lub JPEG. Pomimo że nie jest doskonały, stosuje się go ze względu na prostotę oraz brak ograniczeń patentowych. Jest to przykład wykorzystania algorytmu zachłannego.
Kodowanie Huffmana[edytuj | edytuj kod]

Dany jest alfabet źródłowy (zbiór symboli) oraz zbiór stowarzyszonych z nim prawdopodobieństw Symbolami są najczęściej bajty, choć nie ma żadnych przeszkód żeby było nimi coś innego (np. pary znaków). Prawdopodobieństwa mogą zostać z góry określone dla danego zestawu danych, np. poprzez wyznaczenie częstotliwości występowania znaków w tekstach danego języka. Częściej jednak wyznacza się je indywidualnie dla każdego zestawu danych.
Kodowanie Huffmana polega na utworzeniu słów kodowych (ciągów bitowych), których długość jest odwrotnie proporcjonalna do prawdopodobieństwa Tzn. im częściej dany symbol występuje (może wystąpić) w ciągu danych, tym mniej zajmie bitów.
Własności kodu Huffmana są następujące:
- jest kodem prefiksowym; oznacza to, że żadne słowo kodowe nie jest początkiem innego słowa;
- średnia długość słowa kodowego jest najmniejsza spośród kodów prefiksowych;
- jeśli prawdopodobieństwa są różne, tzn. to długość kodu dla symbolu jest nie większa od kodu dla symbolu
- słowa kodu dwóch najmniej prawdopodobnych symboli mają równą długość.
Kompresja polega na zastąpieniu symboli otrzymanymi kodami.
Algorytm statycznego kodowania Huffmana[edytuj | edytuj kod]
Algorytm Huffmana:
- Określ prawdopodobieństwo (lub częstość występowania) dla każdego symbolu ze zbioru S.
- Utwórz listę drzew binarnych, które w węzłach przechowują pary: symbol, prawdopodobieństwo. Na początku drzewa składają się wyłącznie z korzenia.
- Dopóki na liście jest więcej niż jedno drzewo, powtarzaj:
- Usuń z listy dwa drzewa o najmniejszym prawdopodobieństwie zapisanym w korzeniu.
- Wstaw nowe drzewo, w którego korzeniu jest suma prawdopodobieństw usuniętych drzew, natomiast one same stają się jego lewym i prawym poddrzewem. Korzeń drzewa nie przechowuje symbolu.
Drzewo, które pozostanie na liście, jest nazywane drzewem Huffmana – prawdopodobieństwo zapisane w korzeniu jest równe 1, natomiast w liściach drzewa zapisane są symbole.
Algorytm Huffmana jest algorytmem niedeterministycznym, ponieważ nie określa, w jakiej kolejności wybierać drzewa z listy, jeśli mają takie samo prawdopodobieństwo. Nie jest również określone, które z usuwanych drzew ma stać się lewym bądź prawym poddrzewem. Jednak bez względu na przyjęte rozwiązanie średnia długość kodu pozostaje taka sama.
Na podstawie drzewa Huffmana tworzone są słowa kodowe; algorytm jest następujący:
- Każdej lewej krawędzi drzewa przypisz 0, prawej 1 (można oczywiście odwrotnie).
- Przechodź w głąb drzewa od korzenia do każdego liścia (symbolu):
- Jeśli skręcasz w prawo, dopisz do kodu bit o wartości 1.
- Jeśli skręcasz w lewo, dopisz do kodu bit o wartości 0.
Długość słowa kodowego jest równa głębokości symbolu w drzewie, wartość binarna zależy od jego położenia w drzewie.
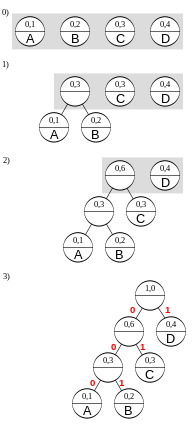
Przykład[edytuj | edytuj kod]
Dany jest zbiór symboli o prawdopodobieństwach wystąpienia odpowiednio
Kodowanie alfabetu źródłowego zgodnie z algorytmem (oznaczenia jak na rysunku obok):
- Łączenie symboli (A) i (B), co powoduje powstanie (A + B) = 0,3; (C) = 0,3; (D) = 0,4.
- Łączenie drzewa (A + B) z symbolem (C), uzyskując elementy ((A + B) + C) = 0,6 i (D) = 0,4.
- Łączenie drzewa ((A + B) + C) z symbolem (D). Teraz pozostaje tylko jeden wolny węzeł (korzeń) – otrzymujemy drzewo (((A + B) + C) + D) = 1,0.
- Pozostaje obliczenie kodów poszczególnych symboli:
- A = lewo, lewo, lewo = 000
- B = lewo, lewo, prawo = 001
- C = lewo, prawo = 01
- D = prawo = 1
Jak łatwo sprawdzić, średnia długość kodu wyniesie:
Jest to mniej niż 2 bity potrzebne w trywialnym kodowaniu o stałej długości znaku. Z kolei entropia źródła wynosi: – optymalne kodowanie powinno charakteryzować się taką właśnie średnią długością kodu. Jednak widać, że jest ona większa – efektywność wynosi w tym przypadku
Dekodowanie jest procesem odwrotnym. Rozpatrywanym ciągiem będzie który zakodowany jest jako Przechodząc drzewo za każdym razem od korzenia do węzła terminalnego, według bitów w kodzie, otrzymuje się odpowiednie symbole:
- 000 [lewy, lewy, lewy] następuje dotarcie do liścia A
- 001 [lewy, lewy, prawy] następuje dotarcie do liścia B
- 01 [lewy, prawy] następuje dotarcie do liścia C
- 1 [prawy] następuje dotarcie do liścia D
Praktyczne zastosowanie[edytuj | edytuj kod]
Jednym z głównych problemów stosowania statycznego algorytmu Huffmana jest konieczność transmisji całego drzewa lub całej tablicy prawdopodobieństw. W przypadku transmisji drzewa węzły są odwiedzane w porządku preorder, węzeł wewnętrzny może zostać zapisany na jednym bicie (ma zawsze dwóch synów), liście natomiast wymagają jednego bitu plus takiej liczby bitów, jaka jest potrzebna do zapamiętania symbolu (np. 8 bitów). Np. drzewo z przykładu powyżej może zostać zapisane jako: (1, 0, ‘D’, 1, 0, ‘C’, 1, 0, ‘B’, 0, ‘A’), czyli 7 + 4 · 8 = 39 bitów.
Lepszą kompresję, kosztem jednak bardzo szybkiego wzrostu wymagań pamięciowych, uzyskuje się, kodując kilka kolejnych znaków naraz, nawet jeżeli nie są one skorelowane.
Przykład kodowania po 2 znaki naraz[edytuj | edytuj kod]
Zbiór symboli jak w poprzednim przykładzie o prawdopodobieństwach wystąpienia odpowiednio Jeśli liczba symboli jest nieparzysta, to należy przyjąć jakąś konwencję postępowania z pierwszym lub ostatnim symbolem. Nie jest to w praktyce duży problem. Następuje kodowanie:
- Łączenie symboli parami – AA, AB, AC, AD, BA, BB, BC, BD, CA, CB, CC, CD, DA, DB, DC, DD o prawdopodobieństwach odpowiednio – {0,01; 0,02; 0,03; 0,04; 0,02; 0,04; 0,06; 0,08; 0,03; 0,06; 0,09; 0,12; 0,04; 0,08; 0,12; 0,16}.
- Drzewo rośnie zgodnie z poniższymi krokami:
- (AA + AB) = 0,03;
- (BA + AC) = 0,05;
- (CA + (AA + AB)) = 0,06;
- (BB + AD) = 0,08;
- (DA + (BA + AC)) = 0,09;
- (BC + CB) = 0,12;
- ((CA + (AA + AB)) + BD) = 0,14;
- (DB + (BB + AD)) = 0,16;
- ((DA + (BA + AC)) + CC) = 0,18;
- (CD + DC) = 0,24;
- ((BC + CB) + ((CA + (AA + AB)) + BD)) = 0,26;
- (DD + (DB + (BB + AD))) = 0,32;
- (((DA + (BA + AC)) + CC) + (CD + DC)) = 0,42;
- (((BC + CB) + ((CA + (AA + AB)) + BD)) + (DD + (DB + (BB + AD)))) = 0,58;
- ((((DA + (BA + AC)) + CC) + (CD + DC)) + (((BC + CB) + ((CA + (AA + AB)) + BD)) + (DD + (DB + (BB + AD))))) = 1,0.
Zatem odpowiednim parom znaków odpowiadają:
- AA – 101010
- AB – 101011
- AC – 00011
- AD – 11111
- BA – 00010
- BB – 11110
- BC – 1000
- BD – 1011
- CA – 10100
- CB – 1001
- CC – 001
- CD – 010
- DA – 0000
- DB – 1110
- DC – 011
- DD – 110
Średnia liczba bitów przypadająca na parę symboli to 3,73, a więc średnia liczba bitów na symbol to 1,865. Jest to znacznie lepsza kompresja (6,75% zamiast 5% przy maksymalnej możliwej 7,68%) niż w poprzednim przykładzie. Używając większej liczby znaków, można dowolnie przybliżyć się do kompresji maksymalnej, jednak znacznie wcześniej wyczerpie się pamięć, ponieważ wymagania pamięciowe rosną wykładniczo do liczby kompresowanych jednocześnie symboli.
Kodowanie Huffmana z mniejszymi wymaganiami pamięciowymi[edytuj | edytuj kod]
Jeśli kodowane są pary symboli (tak jak w przykładzie powyżej) albo trójki symboli, czy ogólnie n-tki symboli, to rozmiar drzewa Huffmana rośnie znacząco – drzewo Huffmana należy zapisać razem z zakodowanym komunikatem, aby można go było zdekodować; zatem im większe drzewo, tym dłuższe stają się kody rzadziej występujących symboli. C. Weaver zaproponował modyfikację algorytmu Huffmana, która redukuje pamięć potrzebną do zapamiętania drzewa. Pomysł został opracowany przez Michaela Hankamera, który opublikował wyniki w artykule „A modified Huffman procedure with reduced memory requirement” (IEEE Transactions on Communication COM-27, 1979, s. 930–932).
Modyfikacja polega na wprowadzeniu dodatkowego symbolu nazywanego ELSE, który zastępuje wszystkie rzadko występujące symbole – jeśli pojedynczy symbol opisuje N bitów, to symbol trafi do zbioru ELSE, gdy jego prawdopodobieństwo Prawdopodobieństwo przypisane do ELSE jest równe sumie zastępowanych przez niego symboli. Przy kodowaniu symbolu należącego do klasy ELSE zapisywany jest kod dla ELSE oraz nieskompresowany symbol; np. gdy kod ELSE to to przy kodowaniu symbolu ‘H’ (kod ASCII ) zapisane zostanie
Dzięki temu drzewo staje się mniejsze, ponieważ zachowuje tylko symbole nienależące do ELSE – co w zupełności wystarczy, ponieważ symbole ze zbioru ELSE są bezpośrednio zapisane w komunikacie. Zastosowanie tej modyfikacji może nawet nieco polepszyć stopień kompresji w stosunku do niezmodyfikowanej wersji algorytmu.
Algorytm dynamicznego kodowania Huffmana[edytuj | edytuj kod]
Dynamiczne kodowanie Huffmana to kodowanie danych o nieznanej statystyce. Statystykę buduje się w miarę napływania danych i co znak lub co daną liczbę znaków poprawia drzewo Huffmana.
Zaletą kodowania dynamicznego jest to, że nie ma potrzeby przesyłania drzewa kodów. Zamiast tego identyczną procedurę poprawiania drzewa muszą przeprowadzać zarówno koder, jak i dekoder.
Istnieją dwa algorytmy pozwalające poprawić drzewo Huffmana:
- algorytm Fallera-Gallagera-Knutha (pomysłodawcami byli Newton Faller i Robert Gallager, metodę ulepszył Donald Knuth),
- algorytm Vittera (dalsze ulepszenia metody FGK opracowane przez Jeffreya Vittera).
U podstaw algorytmu FGK leżą następujące założenia co do formy drzewa:
- każdy węzeł drzewa oprócz liści ma zawsze dwóch potomków;
- z każdym węzłem związany jest licznik: w liściach przechowuje liczbę wystąpień danego symbolu (lub wartość proporcjonalną), w pozostałych węzłach sumę liczników dzieci;
- przy przejściu drzewa wszerz od prawej do lewej i odczycie liczników powiązanych z każdym węzłem uzyskuje się ciąg liczb nierosnących.
W algorytmie Vittera zaostrzone zostało ostatnie założenie:
- również otrzymuje się ciąg liczb nierosnących, lecz w obrębie podciągów o tych samych wartościach na początku znajdują się te pochodzące z węzłów wewnętrznych, a na końcu z liści.
Gdy licznik w jakimś liściu zwiększy się, algorytmy modyfikują (przemieszczając niektóre węzły) jedynie niewielki fragment drzewa, zachowując wyżej wymienione własności. Algorytm Vittera jest nieco bardziej złożony, jednak daje lepsze wyniki, tj. krótsze kody niż algorytm FKG.
Inne algorytmy kompresji bezstratnej[edytuj | edytuj kod]
Zobacz też[edytuj | edytuj kod]
- Asymmetric Numeral Systems
- kod Golomba
- kod unarny
- kod Tunstalla
- kodowanie arytmetyczne
- kodowanie Shannona-Fano
- program do kompresji plików
Przypisy[edytuj | edytuj kod]
- ↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein ↓, s. 383–384.
- ↑ Tim Stephens, Jim Burns: Eminent UCSC computer scientist David Huffman dies at age 74. University of California, Santa Cruz, 1999-10-11. (ang.).
Bibliografia[edytuj | edytuj kod]
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Wprowadzenie do algorytmów. WNT, 2007.
- Generator drzew Huffmana.
- Yann Collet: Finite State Entropy.
Linki zewnętrzne[edytuj | edytuj kod]
- Przetwarzanie sygnałów cyfrowych. dsp.agh.edu.pl. [zarchiwizowane z tego adresu (2016-08-19)]. (materiały dydaktyczne AGH)

















