Tarcie toczne
Tarcie toczne (nazywane również oporem toczenia) – opór ruchu występujący przy toczeniu jednego ciała po drugim. Występuje np. pomiędzy elementami łożyska tocznego, między oponą a nawierzchnią drogi. Zwykle tarcie toczne jest znacznie mniejsze od tarcia ślizgowego występującego między ciałami stałymi, dlatego toczenie jest częstym rodzajem ruchu w technice.
Tarcie toczne występuje na granicy dwóch ciał i dlatego jest sklasyfikowane jako tarcie zewnętrzne[1].
Dynamika zagadnienia[edytuj | edytuj kod]

Siła tarcia tocznego[edytuj | edytuj kod]
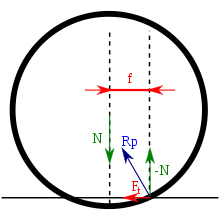
Na toczące się ciało działają siły:
- – przyłożona w środku ciała siła ciągnąca,
- – siła nacisku ciała na podłoże,
- – asymetryczna siła reakcji podłoża.
Gdy suma wektorowa tych sił jest równa zero, to środek walca porusza się ruchem jednostajnym (patrz rysunek nr 1).
Oznacza to że składowa pionowa siły reakcji równoważy siłę nacisku, a składowa pozioma równoważy siłę ciągnącą, przeciwdziałając ruchowi walca, a przez analogię do tarcia ślizgowego nazywana jest siłą tarcia tocznego[2]:


Jednostajne toczenie oznacza także, że suma momentów sił względem dowolnego punktu jest równa zero. Z równowagi momentów sił zilustrowanych na rys. 2 i rys. 3 względem środka walca wynika
z czego wynika:
gdzie:
- – siła tarcia tocznego,
- – współczynnik tarcia tocznego, jego jednostką jest metr,
- – promień toczonego walca,
- – siła nacisku ciała na podłoże.
Wzór ten wynika także z doświadczeń. Proporcjonalność siły tarcia do nacisku oraz do odwrotności promienia ma powyższe uzasadnienie teoretyczne.
Dla niezbyt dużych prędkości toczenia, siła tarcia tocznego nie zależy od prędkości toczenia. Jest to zgodne z trzecim prawem tarcia, mówiącym, że siła tarcia nie zależy od prędkości. Gdy prędkość toczenia jest duża, tak że prędkość powstawania odkształceń jest porównywalna z prędkością rozchodzenia się odkształceń w materiale, opory tarcia tocznego zwiększają się gwałtownie i przewyższają tarcie ślizgowe.
Dla małych prędkości toczenia, niezbyt plastycznych materiałów oraz odkształceń w zakresie sprężystego odkształcenia materiałów wielkość f jest zależna głównie od materiałów podłoża i koła i jest nazywana współczynnikiem tarcia tocznego. Jeżeli są spełnione powyższe warunki, to tarcie toczne (suche) nie zależy od szerokości toczonego ciała.
Moment tarcia tocznego[edytuj | edytuj kod]
Dla toczącego się walca definiuje się moment hamujący ruch obrotowy ciała. Rozpatrując ten moment względem środka obracającego się koła (np. koła samochodu) jest on równy momentowi siły hamującej na ramieniu promienia koła. Rozpatrywany dla toczącego się ciała względem punktu styku toczącego się ciała z podłożem momentowi siły ciągnącej, równoważącej siłę tarcia, na ramieniu o długości promienia toczącego się ciała (rys. 2):
Z drugiej strony, moment tarcia jest równy momentowi siły nacisku na ramieniu o długości równej współczynnikowi tarcia tocznego – rys. 3
gdzie:
- – moment tarcia w N·m,
- – promień toczącego się walca,
- – siła ciągnąca,
- – siła tarcia tocznego,
- – współczynnik tarcia tocznego w metrach.
Wzór na siłę, jak i moment tarcia tocznego, ma zastosowanie tak jak w tarciu suwnym:
- Gdy ciało spoczywa, siła oporu tocznego równoważy siłę ciągnącą, wzór powyższy opisuje maksymalną siłę jaką może przenieść ciało nie poruszając się. Gdy siła ta zostanie przekroczona ciało zacznie toczyć się.
- Gdy ciało toczy się, wzór opisuje siłę jaka przeciwdziała toczeniu się ciała.
Współczynnik tarcia tocznego[edytuj | edytuj kod]
Z powyższego wzoru wynika, że współczynnik tarcia jest zdefiniowany jako iloraz momentu tarcia tocznego do siły nacisku (N):
Graficzna interpretacja współczynnika tarcia tocznego f została przedstawiona na rys. 3 i rys. 4.
Współczynnik tarcia tocznego ma następujące interpretacje fizyczne:
- Gdy ciało spoczywa i nie działa na nie siła ciągnąca, siła reakcji podłoża leży na tej samej prostej co siła nacisku na podłoże. Gdy ciało toczy się, z warunków równowagi wynika, że składowa prostopadła do podłoża siły reakcji podłoża jest siłą równoległą do siły nacisku, ale nie pokrywa się z nią. Współczynnik tarcia tocznego jest równy odległości między prostymi, wzdłuż których działają siła nacisku i składowa pionowa reakcji podłoża (rys. 4).
- Toczące ciało można traktować jako obracające się względem chwilowej osi obrotu (rys. 4 – punkt zaczepienia wektora ), która dla idealnie sztywnych materiałów jest punktem leżącym na prostej przechodzącej przez środek koła i prostopadłej do podłoża. Dla ciał z rzeczywistych materiałów, punkt chwilowego obrotu jest przesunięty w kierunku toczenia się ciała o odległość równą współczynnikowi tarcia.
Orientacyjne wartości współczynnika tarcia dla różnych substancji.
| Koło | Podłoże | Współczynnik tarcia w mm |
|---|---|---|
| drewno miękkie | drewno miękkie | 1,5 |
| drewno miękkie | stal | 0,8 |
| drewno twarde | drewno twarde | 0,8 |
| ebonit | beton | 10–20 |
| ebonit | stal | 7,7 |
| guma | beton | 15–35 |
| hartowana stal | hartowana stal | 0,01 |
| polimer | stal | 2 |
| stal | asfalt | 6 |
| stal | bruk | 1,5 |
| stal | stal | 0,05 |
| żelazo | drewno miękkie | 5,6 |
| żelazo | granit | 2,1 |
| żelazo | żelazo | 0,51 |
| żeliwo | żeliwo | 0,8 |
Opór toczenia[edytuj | edytuj kod]
Oporem toczenia nazywa się siłę jaką toczące się ciało przeciwstawia się toczeniu. Siła oporu toczenia (F) jest proporcjonalna do siły nacisku (N)[3]:
Współczynnik oporów toczenia określany jest między innymi dla kół pojazdów.
Mikroskopowe wyjaśnienie tarcia tocznego[edytuj | edytuj kod]

Opór toczenia nie jest spowodowany tak jak w tarciu ślizgowym zaczepianiem się nierówności, jego przyczyny wynikają z wielu zjawisk zachodzących w trakcie styku, ściskania oraz rozdzielania podłoża i koła. Toczące się ciało styka się z podłożem nie w jednym punkcie, lecz na pewnym obszarze. Jeśli ciało ciągnięte jest „w prawo”, reakcja podłoża nie przypada w miejscu działania nacisku, lecz jest przesunięta w kierunku toczenia, nie jest też skierowana prostopadle w górę, ale jest odchylona od pionu „trochę w lewo”. Składowa pozioma reakcji podłoża ma kierunek przeciwny do siły ciągnącej i hamuje ruch. Takie działanie siły wynika z asymetrii zjawisk zachodzących podczas naciskania i zwalniania nacisku, głównie histerezy sprężystej będącej objawem tarcia wewnętrznego materiałów.
Najważniejsze zjawiska wywołujące tarcie toczne to:
- brak symetrii (histereza sprężysta) oddziaływań przy ściskaniu i rozprężaniu w obszarze styku podłoża i toczonego ciała,
- tworzenie się „wałka” przed toczącym się ciałem i praca tracona na jego tworzenie i pokonywanie,
- tworzenie i rozrywanie połączeń mostkowych (adhezyjnych) między ciałami,
- tarcie suwne – przy dużej powierzchni styku (miękkie materiały) toczące się ciało rozsuwa podłoże z miejsca największego nacisku.
- deformacja plastyczna i przemieszczanie płynów, gdy na styku występuje płyn lub materiały są plastyczne.
Czynniki wpływające na opór toczenia opony[edytuj | edytuj kod]
O oporze toczenia koła z oponą decyduje podłoże, jak i rozpraszanie energii występujące podczas uginania ścian opony.
Niektóre czynniki wpływające na tarcie toczne kola z oponą pneumatyczną:
- Materiał – guma z większą zawartością siarki powoduje mniejszy opór toczenia opony.
- Rozmiar opony – opór toczenia odpowiada ugięciu ścian opony oraz powierzchni kontaktu z podłożem. Przy tym samym ciśnieniu szersze opony rowerowe mają mniejsze ugięcie i z tego powodu mniejszy opór toczenia (aczkolwiek większy opór powietrza).
- Stopień napompowania – mniejsze ciśnienie w oponach skutkuje większym ugięciem ścian opony, a co za tym idzie, większym tarciem tocznym. Tarcie wewnętrzne w odkształcanych ścianach opony powoduje straty energii i może doprowadzić do przegrzania i „wystrzału” opony.
- Za mocno napompowane opony niekoniecznie zmniejszają ogólny opór toczenia, kiedy opona przeskakuje nad nierównościami drogi, energia jest rozpraszana w wyniku poślizgu.
- Ugięcie ścian opony nie jest bezpośrednim wskaźnikiem miary tarcia tocznego. Wysokiej jakości opony z elastyczną osnową umożliwiają znacznie większe odkształcenie przypadające na jednostkę traconej energii niż opony o sztywnych ścianach.
- Rzeźba bieżnika opony ma duży wpływ na opór toczenia. Im „grubszy” wzór bieżnika, tym większy opór toczenia. Dlatego też „szybkie” opony rowerowe mają drobny bieżnik, a ciężarówki zużywają mniej paliwa, kiedy bieżnik jest zużyty.
- Mniejsze koła mają większy opór toczenia niż duże.
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ Wyznaczanie współczynnika tarcia tocznego za pomocą wahadła nachylnego.
- ↑ (PDF)[1].
- ↑ Technika motoryzacyjna – Opory ruchu [online], www.mototechnika.republika.pl [dostęp 2017-11-27].























