Ruch obrotowy

Ruch obrotowy wokół ustalonej osi – szczególny przypadek ruchu obrotowego, rozważany w nauczaniu fizyki. Ograniczenie zagadnienia do stałej osi obrotu wyklucza możliwość opisania takich zjawisk, jak chwianie się lub precesja.
W ruchu obrotowym wokół ustalonej osi, wszystkie punkty bryły poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu, a okręgi te leżą w płaszczyźnie prostopadłej do osi obrotu. Rozważa się obrót punktu materialnego oraz bryły sztywnej wokół ustalonej osi obrotu[1]. Ograniczenie to umożliwia przyjęcie pojęć i sformułowania praw rządzących tym ruchem będących odpowiednikami praw ruchów liniowych. Opis ruchu wokół nieustalonych osi obrotu jest bardziej skomplikowany[2].
Ruch bryły wokół ustalonej osi obrotu często występuje w technice, wiele ruchów można opisać jako złożenie ruchu postępowego i obrotowego względem osi o ustalonym kierunku[1].
Kinematyka[edytuj | edytuj kod]
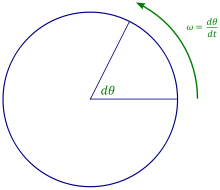
Wybierając do opisu ruchu układ współrzędnych walcowych o osi będącej osią obrotu, jedyną zmieniającą się współrzędną jest kąt o jaki obraca się opisywane ciało. Przez co ruch obrotowy o ustalonej osi obrotu punktu materialnego i bryły sztywnej jest matematycznym odpowiednikiem ruchu postępowego po linii prostej.
Zmiany kąta w czasie opisuje prędkość kątowa określona jako[3]:
Zmiany prędkości kątowej opisuje przyspieszenie kątowe[3]:
gdzie:
- – przyspieszenie kątowe,
- – prędkość kątowa,
- – kąt.
Dynamika[edytuj | edytuj kod]
Podstawowym prawem opisującym ruch bryły sztywnej jest druga zasada dynamiki ruchu obrotowego:
gdzie:
gdzie jest momentem siły względem obranego punktu odniesienia, a – krętem (momentem pędu) względem tego samego punktu odniesienia.
Jeżeli obrót odbywa się względem osi stałej lub sztywnej wówczas druga zasada dynamiki dla ruchu obrotowego może być napisana w następujący sposób:
gdzie oznacza moment siły a moment bezwładności względem osi obrotu.
Gdy brak momentu sił zewnętrznych z pierwszego wzoru można otrzymać równanie ilustrujące zasadę zachowania momentu pędu
Gdy oś obrotu jest ustalona, brak momentu sił oznacza stałość prędkości kątowej, ponieważ
co przy stałości oznacza
Ruch taki nazywany jest jednostajnym ruchem obrotowym.
Zobacz też[edytuj | edytuj kod]
- druga zasada dynamiki ruchu obrotowego
- prędkość obrotowa
- ruch harmoniczny
- ruch postępowy
- ruch posuwisto-zwrotny
Przypisy[edytuj | edytuj kod]
- ↑ a b Resnick i Halliday 1999 ↓, s. 248–249.
- ↑ Resnick i Halliday 1999 ↓, s. 257.
- ↑ a b Resnick i Halliday 1999 ↓, s. 250–252.
Bibliografia[edytuj | edytuj kod]
- Robert Resnick, David Halliday: Podstawy fizyki. Wydawnictwo Naukowe PWN, 1999. ISBN 83-01-09323-4.

















