Kryterium całkowe
Kryterium całkowe (także kryterium całkowe Maclaurina-Cauchy’ego[1]) – kryterium zbieżności szeregów o wyrazach dodatnich oparte na idei porównywania danego szeregu z całką. Wczesna forma tego kryterium została odkryta w Indiach przez Madhawę[2] w XIV wieku i jego następców ze szkoły w Kerali. W Europie kryterium zostało później ponownie odkryte przez Maclaurina w 1742[3] i Cauchy’ego[4].
Kryterium[edytuj | edytuj kod]
Niech będzie funkcją dodatnią i malejącą. Niech ponadto dla każdego Wówczas szereg
(A) |
jest zbieżny wtedy i tylko wtedy, gdy zbieżna jest całka niewłaściwa[5]
(I) |
Interpretacja geometryczna[edytuj | edytuj kod]
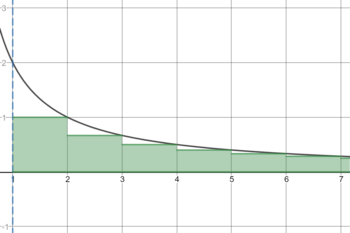
Całka (I) wyraża pole powierzchni pod krzywą (na ilustracji obok zaznaczonej na czarno) na przedziale Wyrazy szeregu (A) podają wielkość rzędnych wykresu w punktach a więc wyrażają pola prostokątów o podstawie i wysokościach (na ilustracji obok zaznaczone na zielono). Suma szeregu (A) jest zatem sumą pól rzeczonych prostokątów. Biorąc to pod uwagę, kryterium całkowe można zinterpretować następująco: jeżeli pole pod wykresem jest skończone, to tym bardziej skończona jest suma pól (równa sumie szeregu (A)). Dokonując przesunięcia każdego z prostokątów o w prawo, wykres na przedziale znajdzie się zawarty w figurze złożonej ze wspomnianych przesunięć. W szczególności, jeżeli pole pod wykresem jest nieskończone, to nieskończone musi być także pole rozważanej figury, a więc i tym samym suma szeregu (A)[6].
Dowód[edytuj | edytuj kod]
Ponieważ funkcja jest malejąca zachodzą nierówności
- dla
- dla
Oznacza to, że
a stąd
W przypadku gdy całka (I) jest zbieżna, ciąg całek częściowych
jest ograniczony, co pociąga ograniczoność ciągu sum częściowych
szeregu (A). Ciąg ten jest także niemalejący (z założenia, że wyrazy szeregu (A) są nieujemne), więc jako ograniczony i niemalejący ciąg liczb rzeczywistych jest on zbieżny, a tym samym szereg (A) jest zbieżny.
W przypadku, gdy szereg (A) jest zbieżny, wyżej zdefiniowany ciąg całek częściowych jest również ograniczony, a więc zbieżny (do całki (I)) jako ograniczony i niemalejący ciąg liczb rzeczywistych[7].
Przykłady zastosowania[edytuj | edytuj kod]
- Szereg harmoniczny rzędu
- jest zbieżny dla Istotnie, funkcja jest dodatnia i malejąca na przedziale więc stosuje się kryterium całkowe:
- gdy czyli gdy [7].
- Szereg
- jest zbieżny dla i rozbieżny w przeciwnym przypadku. Istotnie, oznaczając
- mamy
- a stąd całka niewłaściwa istnieje gdy oraz nie istnieje w przeciwnym przypadku[8].
Przypisy[edytuj | edytuj kod]
- ↑ Fichtenholz 1966 ↓, s. 242.
- ↑ Petrovic 2014 ↓, s. 178.
- ↑ C. Maclaurin, Treatise of fluxions, 1. Edinburgh, 1742.
- ↑ A.L. Cauchy, Sur la convergence des séries, Oeuvres complètes Ser. 2, 7, Gauthier-Villars (1889), s. 267–279.
- ↑ Fichtenholz 1966 ↓, s. 243.
- ↑ Fichtenholz 1966 ↓, s. 244.
- ↑ a b Leja 1971 ↓, s. 276.
- ↑ Leja 1971 ↓, s. 276–277.
Bibliografia[edytuj | edytuj kod]
- Grigorij Michajłowicz Fichtenholz: Rachunek różniczkowy i całkowy. T. 2. Warszawa: Państwowe Wydawnictwo Naukowe, 1966.
- Franciszek Leja: Rachunek różniczkowy i całkowy. Wyd. 11. Warszawa: PWN, 1971.
- John Srdjan Petrovic: Advanced Calculus: Theory and Practice. Boca Raton, London, New York: CRC Press, 2014. ISBN 978-1466565630.





























![{\displaystyle \int \limits _{m}^{\infty }{\frac {\mathrm {d} x}{x^{s}}}=\int \limits _{m}^{\infty }{x^{-s}\mathrm {d} x}=\left[{\frac {x^{-s+1}}{-s+1}}\right]_{m}^{\infty }=\lim _{x\to \infty }~{\frac {x^{-s+1}}{-s+1}}-{\frac {m^{-s+1}}{-s+1}}=-{\frac {m^{-s+1}}{-s+1}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12d1d309dcff6e58a88dba1ecaa19d38cba32df8)






