Diagram kołowy

Ten artykuł należy dopracować:

→ poprawić styl – powinien być encyklopedyczny.
Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu.
Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

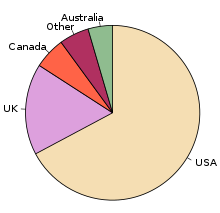
Diagram kołowy (lub wykres/diagram tortowy w wersji 3D) – wykres kołowy podzielony na wycinki, obrazujące proporcje. Na diagramie kołowym długość łuku każdego wycinka (a także kąt środkowy, na którym się opiera, i pole powierzchni, jaki wyznacza) jest proporcjonalna do ilości, jaką przedstawia. Wszystkie wycinki diagramu łącznie tworzą pełne koło. Pokazuje również częstotliwość w pewnych grupach informacji. Nazwa tortowy pochodzi stąd, że wykres tego typu przypomina tort podzielony na kawałki. Najstarszy znany wykres kołowy, został wykonany w 1801 roku przez Williama Playfaira dla Statistical Breviary^[1]^[2].

Diagram kołowy jest prawdopodobnie najczęściej używanym statystycznym wykresem w świecie biznesu i mediów^[3]. Jest jednak krytykowany^[4], a niektórzy zalecają jego unikanie^[5]^[6]^[7]^[8], wskazując między innymi na to, że trudno jest porównać różne sekcje danego wykresu lub dane z różnych wykresów. W niektórych przypadkach diagramy kołowe jasno przedstawiają informacje, w szczególności jeśli celem jest porównanie rozmiaru wycinka do całości, zamiast porównywania wycinków ze sobą^[1]. Diagramy kołowe sprawdzają się najlepiej, jeśli wycinki przedstawiają od 25% do 50% danych^[9]. Wykresy innego typu, takie jak histogram lub wykres kropkowy lub nie-graficzne metody, na przykład tabele, mogą być lepiej dostosowane do przestawiania pewnych informacji.

Zalecane jest przyjęcie za początek podziału promienia koła pozycji „godziny 12” i dokonywanie podziału zgodnie z ruchem wskazówek zegara^[10].

Przykład

Przedstawiony obok przykład diagramu oparty jest o wstępne wyniki wyborów do Parlamentu Europejskiego w 2004 roku. Tabela zawiera liczby mandatów, jakie uzyskała każda grupa polityczna, wraz z ich udziałami we wszystkich dostępnych mandatach wyrażonymi w przybliżeniu w procentach. Wartości w ostatniej kolumnie to miary kątów środkowych każdego wycinka, będące iloczynami miar udziałów i miary kąta pełnego, to jest 360°.

Grupa	Mandaty	Udział (%)	Kąt środkowy (°)
EUL/NGL	39	5,3	19,2
PES	200	27,3	98,4
Greens/EFA	42	5,7	20,7
IND/DEM	15	2,0	7,4
ALDE	67	9,2	33,0
EPP-EP	276	37,7	135,7
UEN	27	3,7	13,3
Inni	66	9,0	32,5
Razem	732	99,9*	360,2*

* z powodu zaokrągleń wyniki nie sumują się do 100 i 360.

Rozmiar każdego kąta środkowego jest proporcjonalny do wielkości odpowiedniej ilości, tutaj: liczby mandatów. Ponieważ wszystkie kąty środkowe mają sumować się do kąta pełnego, który mierzy 360°, kąt środkowy odpowiadający ilości reprezentowanej ułamkiem Q z całości mierzy 360 · Q stopni. W przykładzie kąt środkowy największej grupy politycznej (Europejska Partia Ludowa – Europejscy Demokraci (EPP-EP)) mierzy około 135,7°: 276/732≈0,377, a 0,377·360°≈135,7°.

Użycie, skuteczność i percepcja wzrokowa

Trzy zbiory zaprezentowane przy pomocy diagramów kołowych i histogramów

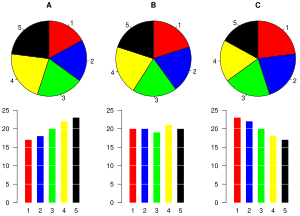
Diagram kołowy jest najczęściej stosowany w biznesie i dziennikarstwie. Statystycy uznają wykresy kołowe za niedokładną metodę prezentacji informacji i są one bardzo rzadko spotykane w literaturze naukowej. Jednym z powodów jest to, że trudno jest porównywać rozmiary elementów na wykresie, na którym zmieniają się pole i kształt zamiast tylko długości. Zgodnie z potęgowym prawem Stevensa pole powierzchni jest postrzegane wzrokowo z siłą 0,7, zaś długość z siłą 1,0. To sugeruje, że długość jest lepszą skalą, ponieważ postrzegane różnice długości są proporcjonalne liniowo do różnic rzeczywistych.

Ponadto w badaniach naukowych na Bell Labs wykazano, że porównania przez kąt były mniej dokładne niż porównania przez długość. Widać to na wykresach po prawej, gdzie są trzy zestawy danych, diagram kołowy i odpowiadający mu histogram poniżej. Większość ma problem z uporządkowaniem wycinków diagramu kołowego względem wielkości, jednak kiedy zastosowany jest histogram, staje się to proste^[11]. Podobnie porównywanie zbiorów danych jest prostsze z użyciem histogramu. Z drugiej strony, jeśli celem jest porównanie danej kategorii (wycinek diagramu) do całości (pełne koło) na jednym wykresie a ich wielkość jest bliska 25% lub 50%, to diagram kołowy może być bardziej skuteczny niż wykres słupkowy.

Warianty

Rozcięty diagram kołowy

Diagram z jednym lub więcej wycinkiem oddzielonym od reszty wykresu. Taki efekt jest używany zarówno aby podkreślić wybrany wycinek, jak również podkreślić mniejsze wycinki wykresu z małych rozmiarów.

Przestrzenny diagram kołowy (trójwymiarowy, 3D)

Użycie perspektywy umożliwia nadanie diagramowi kołowemu wyglądu przestrzennego (3D). Taki zabieg często jest stosowany ze względów estetycznych. Trzeci wymiar nie tylko nie poprawia czytelność wykresu, lecz wręcz przeciwnie, powoduje, że jest trudniejszy w odczycie ze względu na zniekształcenia perspektywiczne umożliwiające odwzorowanie przestrzeni na płaskiej powierzchni. Stosowanie nadmiarowych wymiarów, nie służących do wyświetlania danych, jest niezalecane w ogóle, nie tylko dla wykresów kołowych^[7]^[12].

Diagram pierścieniowy

Diagram pierścieniowy funkcjonalnie jest identyczny z diagramem kołowym. Jedyną różnicą jest to, że jest pozbawiony części środkowej.

Diagram złożony

Nałożenie na siebie dwóch lub więcej diagramów umożliwia zaprezentowanie zmienności zjawiska w czasie (diagram dynamiczny) lub wzajemne porównanie dwóch lub więcej kategorii zjawiska (diagram porównawczy).

Podobne diagramy

Diagram centryczny

„Diagram przyczyny zgonów w armii na Wschodzie” autorstwa Florence Nightingale, 1858

Lech Ratajski wyróżniał szczególne rodzaje diagramów złożonych, wśród nich pochodne diagramów kołowych – diagramy centryczne, centrogramy (ang. polar area diagram – diagram biegunowy). W takich diagramach, inaczej niż w zwykłych diagramach kołowych, poszczególne sektory (wycinki) mają równą wielkość kąta, a wartości odkładane są na osiach rozchodzących się promieniście ze środka^[10].

Taki sposób prezentacji jest często stosowany do zjawisk występujących cyklicznie – koło dzieli się na 12 sekcji odpowiadających np. miesiącom lub godzinom. Zastosował go André-Michel Guerry w 1829, pokazując sezonową zmienność wiatrów w roku oraz urodzeń i zgonów w porach dnia. Złożoną wersję takiego diagramu, ze zmiennością w czasie i podziałem na kategorie zjawiska, przedstawiła Florence Nightingale w 1858, prezentując dla królowej Wiktorii przyczyny zgonów w armii brytyjskiej. Tę formę nazywa się niekiedy diagramem różanym.

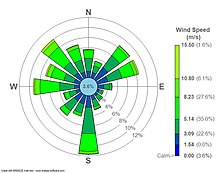
Układ osi diagramu może wskazywać kierunek geograficzny – taki sposób prezentacji przyjęto w klimatologii i meteorologii na wiatrogramach (diagramach wiatrów, różach wiatrów). W ten sposób częstotliwość wiatrów w 1843 zaprezentował Léon Lalanne.

Lech Ratajski zwracał uwagę na to, że w diagramach centrycznych przy traktowaniu wycinka koła jako reprezentacji wartości miarą nie powinna być długość promienia, ale miara powierzchniowa. Przyrost powierzchni wycinka następuje znacznie szybciej (w stosunku kwadratowym) niż przyrost wartości^[10]. Dlatego też w języku angielskim częściej niż w polskim używa się określenia area diagram (diagram powierzchniowy) zamiast zwykłego diagram (wykres, diagram). W zwykłych diagramach kołowych, o stałym promieniu koła, nie ma to znaczenia.

Wykres biegunowy

Oprócz diagramów, Ratajski rozróżniał także wykresy jako graficzne przedstawienie funkcji jednej lub wielu zmiennych, które zawsze jest budowane w układzie współrzędnych, zwykle pokazanych na rysunku. Granica między wykresami a diagramami niekiedy zaciera się, tym niemniej można mówić o wykresach biegunowych (centrycznych) – liniowych, słupkowych i kropkowych. Wśród wykresów biegunowych liniowych wydzielał proste i złożone, sumaryczne i strukturalne oraz ich modyfikacje, jak np. wykresy wskaźnikowe czy amplitudowe^[10]^[13].

Diagram porównawczy dynamiczny (spie)

Wariantem diagramu biegunowego polowego jest wykres spie (ang. spie chart, prawdopodobnie od ang. slice pie – tort warstwowy), opisany przez Drora Feitelsona^[14]. Przez nałożenie na siebie dwóch diagramów centrycznych możliwe jest porównanie danych w dwóch różnych okresach (stanach). Zjawisko w pierwszym stadium prezentowane jest na normalnym diagramie kołowym. W drugim stadium promienie wycinków są zmienione odpowiednio do zmian wartości każdej zmiennej^[15].

Wielopoziomowy diagram kołowy

Wielopoziomowy diagram kołowy jest używany do obrazowania danych hierarchicznych przedstawionych przez koncentryczne okręgi^[16]. Środkowy okrąg przedstawia węzeł główny, z hierarchią oddalającą się od środka. Segment okręgu wewnętrznego (rodzic) przenosi hierarchiczne relacje na te segmenty okręgu zewnętrznego (dzieci), które leżą w zakresie jego wycinka^[17].

Przypisy

↑ ^a ^b Spence (2005).
↑ Tufte, p. 44.
↑ Cleveland, p. 262.
↑ Wilkinson, p. 23.
↑ Tufte, p. 178.
↑ Van Belle, p. 160–162.
↑ ^a ^b Stephen Few. „Save the Pies for Dessert”, August 2007, Retrieved 2010-02-02.
↑ Steve Fenton „Pie Charts Are Bad”.
↑ Good and Hardin, p. 117–118.
↑ ^a ^b ^c ^d Lech Ratajski: Metodyka kartografii społeczno-gospodarczej. Wyd. II. Warszawa: PPWK im. E. Romera, 1989, s. 45–48 i 67–70. ISBN 83-7000-055-X.
↑ Cleveland, p. 86–87.
↑ Good and Hardin, chapter 8.
↑ Przykład na mapie – Wykresy biegunowe. [w:] Internetowy atlas metod kartograficznych [on-line]. 2010–2012. [dostęp 2017-07-16].
↑ Feitelson, Dror (2003) Comparing Partitions With Spie Charts. 2003. [dostęp 2010-08-31].
↑ Przykład – R Graph Gallery: Spie chart. [dostęp 2010-08-31]. [zarchiwizowane z tego adresu (2006-01-04)].
↑ Clark Jeff. (2006). Neoformix. „Multi-level Pie Charts”.
↑ Webber Richard, Herbert Ric, Jiangbc Wel. „Space-filling Techniques in Visualizing Output from Computer Based Economic Models”.

Bibliografia

William S. Cleveland: The Elements of Graphing Data. Pacific Grove, CA: Wadsworth & Advanced Book Program, 1985. ISBN 0-534-03730-5.
Good, Phillip I. and Hardin, James W. Common Errors in Statistics (and How to Avoid Them). Wiley. 2003. ISBN 0-471-46068-0.
Guerry, A.-M. (1829). Tableau des variations météorologique comparées aux phénomènes physiologiques, d’aprés les observations faites à l’obervatoire royal, et les recherches statistique les plus récentes. Annales d’Hygiène Publique et de Médecine Légale, 1:228-.
Robert L. Harris: Information Graphics: A comprehensive Illustrated Reference. Oxford University Press, 1999. ISBN 0-19-513532-6.
Palsky Gilles. Des chiffres et des cartes: la cartographie quantitative au XIXè siècle. Paris: Comité des travaux historiques et scientifiques, 1996. ISBN 2-7355-0336-4.
WilliamW. Playfair WilliamW., Commercial and Political Atlas and Statistical Breviary, HowardH. Wainer, IanI. Spence, Cambridge: Cambridge University Press, 2005, ISBN 0-521-85554-3, OCLC 58604637 .
Spence, Ian. No Humble Pie: The Origins and Usage of a statistical Chart. Journal of Educational and Behavioral Statistics. Winter 2005, 30 (4), 353–368.
Edward R.E.R. Tufte Edward R.E.R., The Visual Display of Quantitative Information, wyd. 2nd ed, Cheshire, Conn.: Graphics Press, 2001, ISBN 0-9613921-4-2, OCLC 46932988 .
van Belle, Gerald. Statistical Rules of Thumb. Wiley, 2002. ISBN 0-471-40227-3.
Wilkinson, Leland. The Grammar of Graphics, 2nd edition. Springer, 2005. ISBN 0-387-24544-8.
Clark Jeff. (2006). „Neoformix”. Multi-level Pie Charts [1]
Webber Richard, Herbert Ric, Jiangbc Wel. Space-filling Techniques in Visualizing Output from Computer Based Economic Models [2]
Stasko John. SunBurst [www.cc.gatech.edu/gvu/ii/sunburst/]
Woodbury, Henry. Nightingales Rose

[Spence2005-1] Spence (2005).

[Tufte,_p._44-2] Tufte, p. 44.

[Cleveland-3] Cleveland, p. 262.

[Wilkinson-4] Wilkinson, p. 23.

[tufte-5] Tufte, p. 178.

[vanbelle-6] Van Belle, p. 160–162.

[sfew-7] Stephen Few. „Save the Pies for Dessert”, August 2007, Retrieved 2010-02-02.

[fenton-8] Steve Fenton „Pie Charts Are Bad”.

[9] Good and Hardin, p. 117–118.

[mk-10] Lech Ratajski: Metodyka kartografii społeczno-gospodarczej. Wyd. II. Warszawa: PPWK im. E. Romera, 1989, s. 45–48 i 67–70. ISBN 83-7000-055-X.

[cleveland85-11] Cleveland, p. 86–87.

[12] Good and Hardin, chapter 8.

[13] Przykład na mapie – Wykresy biegunowe. [w:] Internetowy atlas metod kartograficznych [on-line]. 2010–2012. [dostęp 2017-07-16].

[spie-14] Feitelson, Dror (2003) Comparing Partitions With Spie Charts. 2003. [dostęp 2010-08-31].

[Rspie-15] Przykład – R Graph Gallery: Spie chart. [dostęp 2010-08-31]. [zarchiwizowane z tego adresu (2006-01-04)].

[16] Clark Jeff. (2006). Neoformix. „Multi-level Pie Charts”.

[17] Webber Richard, Herbert Ric, Jiangbc Wel. „Space-filling Techniques in Visualizing Output from Computer Based Economic Models”.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]