Diagram Woronoja

Komórki Woronoja dla losowego zbioru punktów na płaszczyźnie

Diagram Woronoja, tesselacja Dirichleta, tesselacja Woronoja lub komórki Woronoja (ang. Voronoi diagram) – podział płaszczyzny, nazwany tak na cześć twórcy Gieorgija Woronoja (termin tesselacja Dirichleta pochodzi od nazwiska Petera Dirichleta).

W przypadku przestrzeni dwuwymiarowej, dla danego zbioru $n$ punktów, dzieli się płaszczyznę na $n$ obszarów, w taki sposób, że każdy punkt w dowolnym obszarze znajduje się bliżej określonego punktu ze zbioru $n$ punktów, niż od pozostałych $n-1$ punktów

Definicja formalna

Niech $S$ będzie skończonym zbiorem $n$ punktów należących do przestrzeni euklidesowej $E.$ Elementy zbioru $S$ nazwiemy centrami, środkami lub zalążkami.

Obszarem Woronoja lub komórką Woronoja przypisaną pewnemu elementowi $p$ zbioru $S$ nazwiemy zbiór punktów znajdujących się bliżej punktu $p$ niż każdego innego elementu ze zbioru $S{:}$

$Vor_{S}(p)=\{x\in E|\forall q\in S,d(x,p)\leq d(x,q)\},$

gdzie $d$ jest odległością.

Weźmy dwa punkty $a$ i $b$ należące do zbioru $S.$ W przestrzeni dwuwymiarowej $E$ (płaszczyzna) zbiór $\Pi (a,b)$ punktów jednakowo odległych od $a$ i od $b$ jest prostą zwaną symetralną odcinka $ab{:}$

$\Pi (a,b)=\{x\in E|d(x,a)=d(x,b)\}.$

Prosta ta jest granicą między zbiorem punktów mniej oddalonych od punktu $a$ niż od punktu $b$ a zbiorem punktów mniej oddalonych od punktu $b$ niż od punktu $a.$

Niech $H(a,b)$ będzie półpłaszczyzną ograniczoną prostą $\Pi (a,b)$ i zawierającą punkt $a.$ Zawiera więc ona wszystkie punkty bliższe punktowi $a$ niż punktowi $b{:}$

$H(a,b)=\{x\in E|d(x,a)\leq d(x,b)\}.$

Komórką (obszarem) Woronoja przypisaną punktowi $a$ jest przekrój (część wspólna) wszystkich półpłaszczyzn $H(a,b),$ gdzie $b$ zastępuje kolejno każdy punkt ze zbioru $S-\{a\}.$

$Vor_{S}(a)=\bigcap _{b\in S-\{a\}}H(a,b).$

Komórki Woronoja będąc intersekcją półpłaszczyzn są wielobokami wypukłymi. Zbiór tych wieloboków rozbija dwuwymiarową przestrzeń euklidesową $E$ i jest diagramem Woronoja odpowiadającym zbiorowi $S.$

Omówiony podział płaszczyzny na komórki Woronoja można również zastosować w przestrzeni trójwymiarowej. Prosta $\Pi (a,b)$ zastąpiona będzie wówczas płaszczyzną $\Pi (a,b),$ a półpłaszczyzna $H(a,b)$ półprzestrzenią $H(a,b)$ ograniczoną płaszczyzną $\Pi (a,b).$ Przestrzenne komórki Woronoja są wielościanami wypukłymi.

Generalizując, w przestrzeni euklidesowej $N$-wymiarowej, $\Pi (a,b)$ jest hiperpłaszczyzną afiniczną (wymiaru $N-1$), a dowolna komórka Woronoja będąc intersekcją półprzestrzeni $H(a,b)$ wymiaru N, ograniczonych hiperpłaszczyznami $\Pi (a,b)$ jest wielokomórką wypukłą.

Diagram Woronoja (na czerwono) i triangulacja Delone

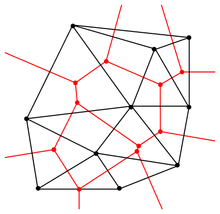
Diagram Woronoja jest grafem dualnym triangulacji Delone, którą można zresztą łatwo otrzymać na podstawie diagramu Woronoja: dwa punkty $p$ i $q$ tworzą krawędź grafu wtedy i tylko wtedy, gdy komórki Woronoja przyporządkowane tym punktom przystają do siebie:

$Del(S)=\{(p,q)\in S^{2}|Vor_{S}(p)\cap Vor_{S}(q)\not =0\}.$

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Voronoi Diagram, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).