Obwiednia (ang. envelope ) – matematyczne pojęcie z zakresu geometrii różniczkowej . Obwiednia rodziny rozmaitości różniczkowych (w szczególności rodziny krzywych lub powierzchni ) jest rozmaitością w każdym swoim punkcie styczną do pewnego członka tej rodziny[1] otoczeniu dowolnego punktu należącego do obwiedni znajdują się zatem zarówno punkty należące do członków tej rodziny, jak i punkty nienależące do żadnego z członków.
Obwiednia powierzchni parametrycznej [ edytuj | edytuj kod ] Obwiednia rodziny prostych Niech dane będzie odwzorowanie p opisujące
(
n
−
1
)
{\displaystyle (n-1)}
powierzchnię zanurzoną w
n
{\displaystyle n}
t
:
{\displaystyle t{:}}
R
n
−
1
×
R
⊃
U
∋
(
u
,
t
)
↦
p
(
u
,
t
)
∈
R
n
{\displaystyle \mathbb {R} ^{n-1}\times \mathbb {R} \supset U\ni (\mathbf {u} ,t)\mapsto \mathbf {p} (\mathbf {u} ,t)\in \mathbb {R} ^{n}}
Obwiednią E powierzchni p względem parametru
t
{\displaystyle t}
∂
p
∂
t
(
u
,
t
)
∈
T
p
(
u
,
t
)
{\displaystyle {\frac {\partial \mathbf {p} }{\partial t}}(\mathbf {u} ,t)\in T_{\mathbf {p} (\mathbf {u} ,t)}}
gdzie
T
p
(
u
,
t
)
{\displaystyle T_{\mathbf {p} (\mathbf {u} ,t)}}
liniową podprzestrzenią styczną do powierzchni
p
{\displaystyle \mathbf {p} }
p
(
u
,
t
=
c
o
n
s
t
)
.
{\displaystyle \mathbf {p} (\mathbf {u} ,t=\mathrm {const} ).}
∂
p
∂
u
i
{\displaystyle {\frac {\partial \mathbf {p} }{\partial u^{i}}}}
i
=
0
,
…
,
n
−
1
{\displaystyle i=0,\dots ,n-1}
det
[
∂
p
0
∂
t
∂
p
0
∂
u
0
⋯
∂
p
0
∂
u
n
−
1
∂
p
1
∂
t
∂
p
1
∂
u
0
⋯
∂
p
1
∂
u
n
−
1
⋮
⋮
⋱
⋮
∂
p
n
∂
t
∂
p
n
∂
u
0
⋯
∂
p
n
∂
u
n
−
1
]
=
0
{\displaystyle \det \left[{\begin{array}{c}{\frac {\partial p^{0}}{\partial t}}&{\frac {\partial p^{0}}{\partial u^{0}}}&\cdots &{\frac {\partial p^{0}}{\partial u^{n-1}}}\\{\frac {\partial p^{1}}{\partial t}}&{\frac {\partial p^{1}}{\partial u^{0}}}&\cdots &{\frac {\partial p^{1}}{\partial u^{n-1}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial p^{n}}{\partial t}}&{\frac {\partial p^{n}}{\partial u^{0}}}&\cdots &{\frac {\partial p^{n}}{\partial u^{n-1}}}\end{array}}\right]=0}
Dla przypadku trójwymiarowego (n=3) równanie obwiedni powierzchni
p
(
u
,
v
,
t
)
∈
R
3
{\displaystyle \mathbf {p} (u,v,t)\in \mathbb {R} ^{3}}
det
[
∂
p
∂
t
(
u
,
v
,
t
)
∂
p
∂
u
(
u
,
v
,
t
)
∂
p
∂
v
(
u
,
v
,
t
)
]
=
0
{\displaystyle \det \left[{\begin{array}{c}{\frac {\partial \mathbf {p} }{\partial t}}(u,v,t)&{\frac {\partial \mathbf {p} }{\partial u}}(u,v,t)&{\frac {\partial \mathbf {p} }{\partial v}}(u,v,t)\end{array}}\right]=0}
Powyższe równanie może być zapisane z użyciem iloczynu skalarnego wektora
∂
p
∂
t
{\displaystyle {\tfrac {\partial \mathbf {p} }{\partial t}}}
wektora normalnego
n
{\displaystyle n}
p w punkcie
(
u
,
v
)
:
{\displaystyle (u,v){:}}
⟨
∂
p
∂
t
,
n
(
u
,
v
)
⟩
=
0
{\displaystyle \left\langle {\tfrac {\partial \mathbf {p} }{\partial t}},\mathbf {n} (u,v)\right\rangle =0}
gdzie
n
(
u
,
v
)
{\displaystyle n(u,v)}
iloczynem wektorowym pochodnych cząstkowych odwzorowania p :
n
(
u
,
v
)
=
∂
p
∂
u
×
∂
p
∂
v
{\displaystyle \mathbf {n} (u,v)={\frac {\partial \mathbf {p} }{\partial u}}\times {\frac {\partial \mathbf {p} }{\partial v}}}
Obwiednią poruszającego się wzdłuż osi OX jednostkowego okręgu w dwuwymiarowej przestrzeni OXY są dwie proste
y
=
−
1
{\displaystyle y=-1}
y
=
1
{\displaystyle y=1}
Jednostkowy okrąg poruszający się ruchem prostoliniowym wzdłuż osi OX w przestrzeni dwuwymiarowej OXY jest sparametryzowany kątem
α
:
{\displaystyle \alpha {:}}
p
(
α
,
t
)
=
(
cos
α
+
t
,
sin
α
)
{\displaystyle \mathbf {p} (\alpha ,t)=(\cos \alpha +t,\sin \alpha )}
pochodne cząstkowe względem
α
{\displaystyle \alpha }
t
{\displaystyle t}
∂
p
∂
α
=
(
−
sin
α
,
cos
α
)
{\displaystyle {\frac {\partial \mathbf {p} }{\partial \alpha }}=(-\sin \alpha ,\cos \alpha )}
∂
p
∂
t
=
(
1
,
0
)
{\displaystyle {\frac {\partial \mathbf {p} }{\partial t}}=(1,0)}
Równanie obwiedni ma zatem postać:
det
[
−
sin
α
1
cos
α
0
]
=
0
⇔
cos
α
=
0
⇔
α
=
π
2
+
n
π
{\displaystyle \det \left[{\begin{array}{c}-\sin \alpha &1\\\cos \alpha &0\end{array}}\right]=0\Leftrightarrow \cos \alpha =0\Leftrightarrow \alpha ={\frac {\pi }{2}}+n\pi }
zaś samą obwiednię stanowią dwie proste
y
=
1
{\displaystyle y=1}
y
=
−
1
{\displaystyle y=-1}
Obwiednia powierzchni implicite [ edytuj | edytuj kod ] Niech dana będzie powierzchnia w przestrzeni
n
{\displaystyle n}
F
(
p
,
t
)
=
0
{\displaystyle F(\mathbf {p} ,t)=0}
gdzie
p
∈
R
n
,
{\displaystyle \mathbf {p} \in \mathbb {R} ^{n},}
t
∈
R
{\displaystyle t\in \mathbb {R} }
F
:
R
n
×
R
↦
R
.
{\displaystyle F:\mathbb {R} ^{n}\times \mathbb {R} \mapsto \mathbb {R} .}
E powierzchni opisanej przy pomocy
F
{\displaystyle F}
(
p
,
t
)
,
{\displaystyle (\mathbf {p} ,t),}
∂
F
∂
t
(
p
,
t
)
=
0
∧
F
(
p
,
t
)
=
0
{\displaystyle {\frac {\partial F}{\partial t}}(\mathbf {p} ,t)=0\wedge F(\mathbf {p} ,t)=0}
Jednostkowy okrąg poruszający się ruchem prostoliniowym wzdłuż osi OX w przestrzeni dwuwymiarowej OXY opisany jest za pomocą:
F
(
x
,
y
,
t
)
=
(
x
−
t
)
2
+
y
2
−
1
=
0
{\displaystyle F(x,y,t)=(x-t)^{2}+y^{2}-1=0}
Pochodna cząstkowa
F
{\displaystyle F}
t
{\displaystyle t}
∂
F
∂
t
=
−
2
(
x
−
t
)
{\displaystyle {\frac {\partial F}{\partial t}}=-2(x-t)}
Równanie obwiedni ma zatem postać:
{
F
(
x
,
y
,
t
)
=
(
x
−
t
)
2
+
y
2
−
1
=
0
∂
F
∂
t
(
x
,
y
,
t
)
=
−
2
(
x
−
t
)
=
0
{\displaystyle \left\{{\begin{array}{l}F(x,y,t)=(x-t)^{2}+y^{2}-1=0\\{\frac {\partial F}{\partial t}}(x,y,t)=-2(x-t)=0\end{array}}\right.}
z czego wynika, iż samą obwiednię stanowią dwie proste
(
x
=
t
,
y
=
±
1
)
.
{\displaystyle (x=t,y=\pm 1).}
Flaquer J., Garate G., Pargada M.: Envelopes of moving quadric surfaces , CAGD 9, 1992.
Eisenhart L.P.: A Treatise on the Differential Geometry of Curves and Surfaces , Dover 2004. Eric W. E.W. Weisstein Eric W. E.W. , Envelope MathWorld , Wolfram Research [dostęp 2020-12-12] (ang. ) . 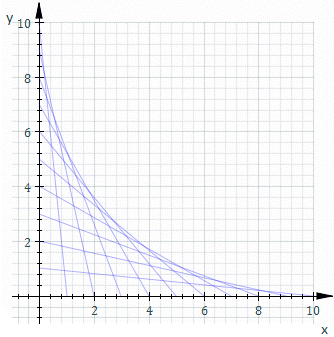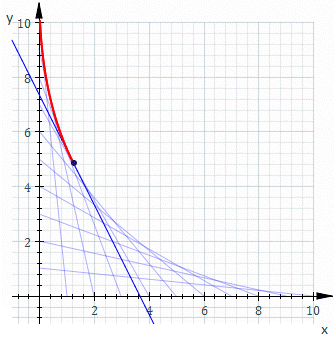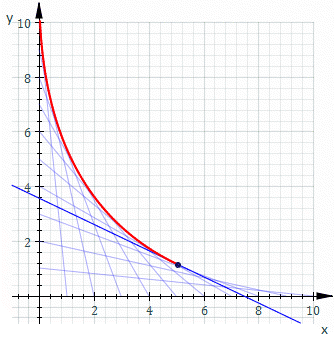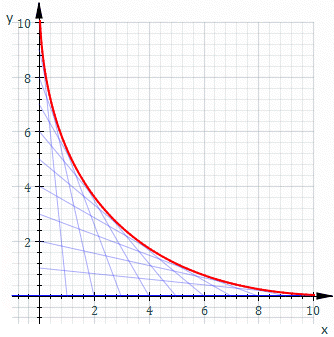













![{\displaystyle \det \left[{\begin{array}{c}{\frac {\partial p^{0}}{\partial t}}&{\frac {\partial p^{0}}{\partial u^{0}}}&\cdots &{\frac {\partial p^{0}}{\partial u^{n-1}}}\\{\frac {\partial p^{1}}{\partial t}}&{\frac {\partial p^{1}}{\partial u^{0}}}&\cdots &{\frac {\partial p^{1}}{\partial u^{n-1}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial p^{n}}{\partial t}}&{\frac {\partial p^{n}}{\partial u^{0}}}&\cdots &{\frac {\partial p^{n}}{\partial u^{n-1}}}\end{array}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a19a3a4336342187bcc5847cd33d6f9c9a2822)

![{\displaystyle \det \left[{\begin{array}{c}{\frac {\partial \mathbf {p} }{\partial t}}(u,v,t)&{\frac {\partial \mathbf {p} }{\partial u}}(u,v,t)&{\frac {\partial \mathbf {p} }{\partial v}}(u,v,t)\end{array}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b63c77b7634bcd01428d620419350745d7513c66)












![{\displaystyle \det \left[{\begin{array}{c}-\sin \alpha &1\\\cos \alpha &0\end{array}}\right]=0\Leftrightarrow \cos \alpha =0\Leftrightarrow \alpha ={\frac {\pi }{2}}+n\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a8156518ff0582a39d3a23ce0c8bbadc16f92f6)










