Konstrukcje klasyczne
| Ten artykuł należy dopracować |
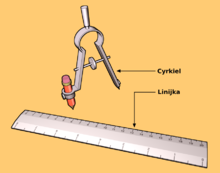
Konstrukcje klasyczne, konstrukcje platońskie[1][2], konstrukcje przy użyciu cyrkla i liniału – wspólna nazwa problemów polegających na wyznaczeniu odcinków lub kątów spełniających dane warunki jedynie przy pomocy cyrkla i linijki bez podziałki (liniału).
Zasady konstrukcji[edytuj | edytuj kod]
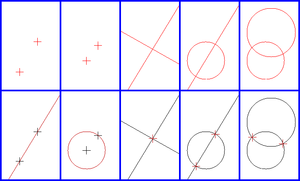
Obydwa narzędzia są wyidealizowane – cyrkiel może być rozwarty na dowolną szerokość, a linijka jest jednostronna (tj. nie wolno korzystać z drugiej krawędzi) i ma potencjalnie nieskończoną długość. Jedyne dozwolone wykorzystanie cyrkla to kreślenie okręgów o środkach w punktach, które już są dane i promieniach równych odcinkom wyznaczonym przez dane lub już skonstruowane punkty; jedyne dozwolone wykorzystanie linijki to rysowanie (lub przedłużanie) odcinków wyznaczonych przez dane lub już skonstruowane punkty. Poza tym mając dane:
- dwie proste,
- prostą i okrąg,
- dwa okręgi,
można znaleźć ich punkty wspólne lub stwierdzić, że ich nie ma. Inne czynności są niedozwolone.
Słynne problemy starożytności[edytuj | edytuj kod]

Trzy słynne problemy starożytnej matematyki greckiej: trysekcja kąta (podział danego kąta na trzy równe części), podwojenie sześcianu (wyznaczenie krawędzi sześcianu o objętości dwa razy większej niż sześcian dany) i kwadratura koła (konstrukcja kwadratu o polu równym polu danego koła) nie mogą być rozwiązane przy pomocy cyrkla i linijki[1], ale dowód tego podany został dopiero w roku 1837 przez Pierre’a Wantzela i jest wnioskiem z twierdzenia noszącego dziś jego imię. Konstrukcje te mogą być jednak rozwiązane w przybliżeniu z dowolną założoną dokładnością. Podejmowano również próby zrealizowania innych niewykonywalnych konstrukcji, np. siedmiokąta foremnego czy powiązanej z kwadraturą koła rektyfikacji okręgu (konstrukcji odcinka o długości równej obwodowi danego okręgu).
Konstrukcje samą linijką[edytuj | edytuj kod]
Jeśli dana konstrukcja jest wykonalna za pomocą cyrkla i linijki, to jest ona wykonalna za pomocą samej linijki, o ile dany jest na płaszczyźnie pewien okrąg wraz ze środkiem (twierdzenie Ponceleta-Steinera)[3].
Konstrukcje samym cyrklem[edytuj | edytuj kod]
Jeżeli dana konstrukcja geometryczna jest wykonalna za pomocą cyrkla i linijki, to jest wykonalna za pomocą samego cyrkla, pod warunkiem, że ograniczy się do wyznaczania punktów konstrukcji, a pominie rysowanie linii (twierdzenie Mohra-Mascheroniego)[1].
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ a b c Encyklopedia szkolna ↓, s. 108.
- ↑ konstrukcja geometryczna, [w:] Encyklopedia PWN [dostęp 2024-03-18].
- ↑ Encyklopedia szkolna ↓, s. 109.
Bibliografia[edytuj | edytuj kod]
- Matematyka, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990 (Encyklopedia szkolna), s. 108, ISBN 83-02-02551-8.
Linki zewnętrzne[edytuj | edytuj kod]
- Eric W. Weisstein, Geometric Construction, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2024-03-07].
