Trójkąt Maxwella

Trójkąt Maxwella, trójkąt barw – sporządzony w połowie XIX w. przez Jamesa Clerka Maxwella wykres trójkątny, ilustrujący sposób otrzymywania różnych barw przez odpowiednie połączenie trzech barw podstawowych: czerwonej (R, ang. red), zielonej (G, ang. green) i niebieskiej (B, ang. blue), umieszczonych w wierzchołkach trójkąta. Wykres – po modyfikacjach – stał się podstawą technologii kolorowego druku, fotografii i telewizji barwnej (zob. RGB, CIEXYZ).

Tło historyczne

Stan wiedzy o naturze światła w czasach badań Maxwella ilustruje jego zdanie:

„	Chyba nie można uniknąć wniosku, że światło polega na poprzecznym falowaniu tego samego ośrodka, który wywołuje zjawiska elektryczne i magnetyczne.	”
— James Clerk Maxwell, [Wikicytaty]

Maxwell dokonał przełomowej unifikacji teorii magnetyzmu i elektryczności (zob. pole elektromagnetyczne, równania Maxwella). W dziedzinie systematyki barw kontynuował badania rozpoczęte przez Isaaca Newtona w XVII w. (niemal 200 lat przed odkryciem natury światła) opracowaniem pierwszego systemu barw – „koła barw” (zob. historia tarczy Newtona).

Dalsze badania widzenia barwnego były prowadzone w XVIII i XIX w. przez wielu innych fizyków, chemików i lekarzy, m.in. Michaiła Łomonosowa (1711–1765), Johna Daltona (1766–1844), Thomasa Younga (1773–1829), Hermanna Grassmanna (1809–1877), Hermanna von Helmholtza (1821–1894), Lorda Rayleigha (1842–1919), Ernsta Abbego (1840–1905), Alberta Koeniga i wielu innych. Próby systematyki barw podejmował również Johann Wolfgang von Goethe (jego dzieło Farbenlehre uznaje się za pierwszą „psychologię kolorów”).

Z punktu widzenia nauk ścisłych i dzisiejszych modeli syntezy barw najistotniejsze było zgromadzenie wiedzy o:

• promieniowaniu elektromagnetycznym,
• anatomii oka oraz fizjologii i psychofizjologii wzroku i innych zmysłów.

Zostały sformułowane np.:

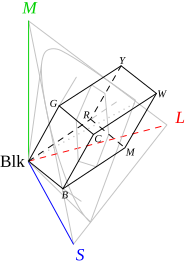
• teoria trichromatyczna Younga-Helmholtza, wiążąca powstawanie wrażeń barwnych z istnieniem w siatkówce oka trzech rodzajów czopków, absorbujących światło w trzech różnych zakresach długości fali – długich (L, X, czerwony), średnich (M, Y, zielony) i krótkich (S, Z, niebieski),
• prawa Grassmana, który wskazał możliwości nadania procesom dodawania i odejmowania barw, jakościowo opisywanemu już przez Newtona, formy matematycznej.

Badania Maxwella i trójkąt barw

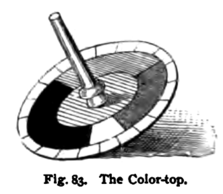
Maxwell wykonał doświadczenia z użyciem wirującego krążka, przypominającego koło barw Newtona (zob. tarcza Newtona), wydzielając jednak na okręgu nie 7 lecz tylko 3 barwne sektory, o kolorach zgodnych z trichromatyczną teorią Younga-Helmholtza. Zastosował barwy zasadnicze (podstawowe):

• czerwoną (R, λ = 630 nm),
• zieloną (G, λ = 538 nm),
• niebieską (B, λ = 457 nm),

dobierając długości fal (λ) na podstawie dostępnych wówczas wyników badań w dziedzinie fizjologii wzroku (m.in. ślepoty barw). Na tarczy dysku umieścił trzy krążki o jednakowej wielkości, przecięte wzdłuż promienia i nałożone na siebie tak, aby była możliwa swobodna zmiana wielkości sektorów. Ich względne wielkości odpowiadały względnym udziałom odpowiednich wiązek promieniowania w mieszaninie docierającej do oka. Na tarczy umieszczał ponadto dodatkowy, mniejszy krążek, o barwie, którą odtwarzał.

W czasie doświadczeń przede wszystkim określił względne udziały barw zasadniczych (r, g, b) w chwili, gdy odbierał wrażenie bieli (W), co zapisał jako:

$W = r R + g G + b B,$

gdzie:

$r = \frac{R}{R + G + B},$

$g = \frac{G}{R + G + B},$

$b = \frac{B}{R + G + B}.$

W kolejnych etapach eksperymentu zmieniał jedną z barw zasadniczych na inną, np. czerwoną (R) na żółtą (Y), i powtarzał określanie udziałów odpowiadających bieli:

$W = y Y + g' G + b' B.$

Porównując prawe strony obu równań otrzymywał zależność definiującą odtwarzaną barwę złożoną, np.:

$r R + g G + b B = y Y + g' G + b' B,$

$Y = \frac{r}{y} R + \frac{g - g'}{y} G + \frac{b - b'}{y} B.$

W analogiczny sposób Maxwell określił wartości współczynników udziału barw zasadniczych dla każdej z barw złożonych widma. Obliczenia potwierdził eksperymentalnie – po odpowiednim ustawieniu wielkości sektorów R, G i B barwy obu pól – zewnętrznego (mieszanina wiązek R, G i B) i wewnętrznego (odtwarzana barwa złożona lub prosta) były jednakowe.

James Clerk Maxwell ok. 1895 r.

Dysk barw (złożenie 3. naciętych barwnych krążków)

Trójkąt barw Maxwella [Color and its applications, 1921 r.]

Względna absorpcja światła przez czopki K, Ś, D (ang. S, M i L) i pręciki (Pr) siatkówki oka

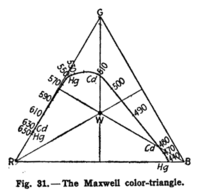
Wyniki oznaczeń współczynników udziału barw R, G i B dla różnych barw złożonych Maxwell przedstawił na wykresie trójkątnym – trójkącie równoramiennym, w którego wierzchołkach znajdują się barwy zasadnicze, a boki odpowiadają mieszaninom dwóch barw, połączonych w różnych proporcjach. Punkt w polu takiego wykresu jest wyznaczony przez wartości r, g i b. Na skonstruowanym przez Maxwella wykresie punkty odpowiadające barwom widmowym (monochromatycznym) znalazły się na zewnątrz pola – na linii opisującej trójkąt, co wpłynęło na położenie wyznaczonych linii zależności współczynników udziału barw zasadniczych od długości fali. Krzywe współczynników udziału barwy czerwonej, zielonej i niebieskiej, otrzymane przez Maxwella, przypominają znane obecnie widma absorpcji promieniowania przez czopki L, M i S, na krzywych Maxwella występują jednak zakresy λ, w których współczynniki mają niewielkie wartości ujemne (wszystkie punkty wewnątrz i na bokach trójkąta odpowiadają barwom nienasyconym).

Zastosowania trójkąta Maxwella

Zaproponowana przez Maxwella systematyka barw była podstawą prac jego następców, dysponujących doskonalszymi technikami pomiarów i obliczeń. W pierwszej połowie XX w. zajmowali się tym problemem m.in. A. Koenig, C. Dieterici, D.B. Judd, W.D. Wright, J. Guild. Badania doprowadziły do ustalenia w roku 1931 przez Międzynarodową Komisję Oświetleniową (Comission Internationale de l'Eclairage) znormalizowanego systemu kolorymetrycznego. System CIE 1931, wywodzący się z trójkąta Maxwella, opiera się na uznaniu za podstawowe barw widmowych o długościach 700, 546 i 436 nm. Barwy są opisywane w układzie współrzędnych trójchromatycznych X, Y, Z, zwanych też względnymi sprawnościami wizualnymi czopków.

Trójkąt Maxwella w przestrzeni barw CIEXYZ, 1931 r.

Trójwymiarowa przestrzeń barw
Gamut:
S, M, L – λ krótkie, średnie, długie
R, G, B, C, M, Y, W, Blk – odpowiednio:
czerwony, zielony, niebieski, cyjan, magenta, żółty, biały, czarny