Trochoida
Trochoida (gr. trochós – koło, eídos – kształt) – krzywa płaska zakreślona przez dowolnie obrany punkt stale związany z kołem toczącym się wzdłuż wewnętrznej lub zewnętrznej strony stałego (nie poruszającego się) okręgu bez poślizgu[1]. Termin został wprowadzony do matematyki przez Gilles’a de Robervala.
Jeśli punkt pokrywa się ze środkiem toczącego się koła, wówczas poruszając się zakreśla okrąg. W pozostałych przypadkach tor ruchu to krzywa (trochoida).
Charakterystyka trochoid[edytuj | edytuj kod]
Wyróżnia się 6 typów trochoid, a ich nazwa zależy od dwóch czynników:
- Odległość punktu od środka toczącego się koła ( )
- Wzajemne położenie koła poruszającego się i koła stałego na płaszczyźnie. Istnieją dwie możliwości:
- jeśli toczące się koło znajduje się wewnątrz koła stałego, wówczas nazwy trochoid rozpoczynają się przedrostkiem hipo- (gr. hypó – pod, poniżej),
- jeśli porusza się ono wzdłuż zewnętrznej strony koła stałego, nazwy mają przedrostek epi- (gr. epí – na, do).
Hipocykloida[edytuj | edytuj kod]
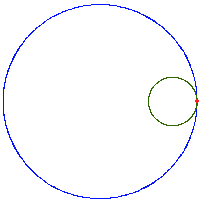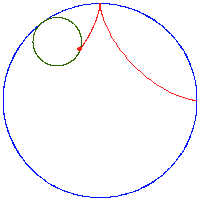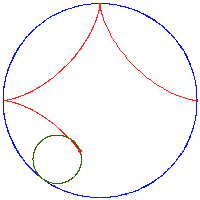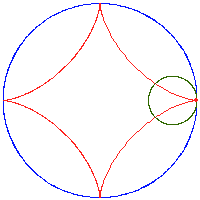
Cechy charakterystyczne:
- punkt leży na obwodzie koła
- hoło toczy się wzdłuż wewnętrznej strony koła stałego,
- hipocykloida opisywana jest równaniami parametrycznymi:
Hipotrochoida[edytuj | edytuj kod]
Wspólna nazwa hipocykloidy skróconej i hipocykloidy wydłużonej.
- Uwaga
- niektóre źródła[2] uznają pojęcie hipotrochoida za synonim hipocykloidy skróconej.
Hipocykloida skrócona[edytuj | edytuj kod]
Cechy charakterystyczne:
- punkt leży wewnątrz koła na jego promieniu
- koło toczy się wzdłuż wewnętrznej strony koła stałego,
- hipotrochoidę najłatwiej opisać równaniami parametrycznymi:
Hipocykloida wydłużona[edytuj | edytuj kod]

Cechy charakterystyczne:
- punkt leży na zewnątrz koła
- koło toczy się wzdłuż wewnętrznej strony koła stałego,
- hipocykloidę wydłużoną opisuje się tymi samymi równaniami parametrycznymi, co hipotrochoidę:
Epicykloida[edytuj | edytuj kod]

Cechy charakterystyczne:
- punkt leży na obwodzie koła
- koło toczy się wzdłuż zewnętrznej strony koła stałego,
- epicykloidę opisuje się równaniami parametrycznymi:
Epitrochoida[edytuj | edytuj kod]
Wspólna nazwa epicykloidy skróconej i epicykloidy wydłużonej.
- Uwaga
- niektóre źródła uznają pojęcie epitrochoida za synonim epicykloidy skróconej.
Epicykloida skrócona[edytuj | edytuj kod]

Cechy charakterystyczne:
- punkt leży wewnątrz koła na jego promieniu
- koło toczy się wzdłuż zewnętrznej strony koła stałego,
- epicykloidę skróconą opisuje się równaniami parametrycznymi:
Epicykloida wydłużona[edytuj | edytuj kod]
- punkt leży na zewnątrz koła
- koło toczy się wzdłuż zewnętrznej strony koła stałego,
- epicykloidę wydłużoną opisuje się równaniami:
Krzywa otwarta[edytuj | edytuj kod]
- Jeżeli stosunek jest liczbą niewymierną, wykreśloną przez punkt krzywą nazywamy krzywą otwartą.
Zobacz też[edytuj | edytuj kod]
Przypisy[edytuj | edytuj kod]
- ↑ trochoida, [w:] Encyklopedia PWN [dostęp 2021-09-29].
- ↑ Hipotrochoida - Zapytaj.onet.pl [online], portalwiedzy.onet.pl [dostęp 2017-11-27] [zarchiwizowane z adresu 2006-06-16] (pol.).
Bibliografia[edytuj | edytuj kod]
- http://www.algorytm.org/index.php?option=com_content&task=view&id=52&Itemid=28
- http://www.wiki.artlink.pl/T/0/39372/TROCHOIDA/
- http://www.swo.pwn.pl/haslo.php?id=28019
- https://web.archive.org/web/20081024151645/http://megabajt.net/n_matematyka/fp01.htm
- hipotrochoida, [w:] Encyklopedia PWN [dostęp 2009-05-30].



















