Gra w życie

Glider gun

Gra w życie (Life, The game of life) – jeden z pierwszych i najbardziej znanych przykładów automatu komórkowego, wymyślony w roku 1970 przez brytyjskiego matematyka Johna Conwaya.

Tor wyścigowy w Grze w Życie

Gra została spopularyzowana przez Martina Gardnera na łamach Scientific American. Od momentu publikacji zawsze wzbudzała duże zainteresowanie z powodu zaskakującego sposobu, w jaki struktury potrafią ewoluować. To właśnie jej pojawienie się wzbudziło zainteresowanie automatami komórkowymi wśród studentów, którzy traktowali ją jako rozrywkę oraz fizyków, którzy zwrócili uwagę na możliwości automatów w zakresie symulatorów fizycznych. Dzisiaj matematyków, ekonomistów i naukowców z innych dziedzin interesuje sposób, w jaki przy zastosowaniu tylko kilku prostych reguł powstają skomplikowane struktury.

Powstanie gry

Conway zainspirowany pracami Stanisława Ulama, Roberta Schrandta oraz nad układami sąsiadów i regułami zmian, eksperymentował nad stworzeniem takiego automatu pod koniec lat 60. XX wieku. Reguły, które w ostateczności przyczyniły się do powstania gry Życie zostały wybrane, ponieważ pozwalały na równowagę pomiędzy zbyt szybkim rozrastaniem się struktur i zbyt wolnym pojawianiem się szybko znikających obiektów. Do badania populacji żyjących Conway używał komputera PDP-7.

Opis reguł gry

Gra toczy się na nieskończonej planszy (płaszczyźnie) podzielonej na kwadratowe komórki. Każda komórka ma ośmiu „sąsiadów” (tzw. sąsiedztwo Moore’a), czyli komórki przylegające do niej bokami i rogami. Każda komórka może znajdować się w jednym z dwóch stanów: może być albo „żywa” (włączona), albo „martwa” (wyłączona). Stany komórek zmieniają się w pewnych jednostkach czasu. Stan wszystkich komórek w pewnej jednostce czasu jest używany do obliczenia stanu wszystkich komórek w następnej jednostce. Po obliczeniu wszystkie komórki zmieniają swój stan dokładnie w tym samym momencie. Stan komórki zależy tylko od liczby jej żywych sąsiadów. W grze w życie nie ma graczy w dosłownym tego słowa znaczeniu. Udział człowieka sprowadza się jedynie do ustalenia stanu początkowego komórek.

Zdefiniowano kilka wzorców reguł generowania, najbardziej rozpowszechnione są reguły wymyślone przez Conwaya. Do nich też odnosi się podział struktur, przedstawiony w dalszej części artykułu.

Reguły gry według Conwaya

• Martwa komórka, która ma dokładnie 3 żywych sąsiadów, staje się żywa w następnej jednostce czasu (rodzi się);
• Żywa komórka z 2 albo 3 żywymi sąsiadami pozostaje nadal żywa; przy innej liczbie sąsiadów umiera (z „samotności” albo „zatłoczenia”).

Szczegółowy podział struktur ze względu na zachowanie

Niezmienne

Struktury niezmienne, inaczej stabilne lub statyczne, pozostają identyczne bez względu na krok czasowy (dla każdej żywej komórki spełniony jest warunek przetrwania i dla żadnej spośród martwych nie jest spełniony); najprostsza taka struktura (block) składa się z 4 żywych komórek. Pojawiają się bardzo często jako produkty końcowe ewolucji struktur. Tworzy się je stosunkowo prosto, istnieją schematy według których można wymyślać nowe tego typu struktury.

• 
  Klocek (blok)
• 
  Łódź
• 
  Bochenek
• 
  Kryształ (ang. beehive – ul)
• 
  Koniczynka (ang. tub – kadź)
• 
  Staw (ang. pond)

Oscylatory

Oscylatory zmieniają się okresowo, co pewien czas powracają do swojego stanu pierwotnego; najprostsza taka struktura składa się z trzech żywych komórek położonych w jednym rzędzie. Najprostsze z nich dość często pojawiają się jako produkty końcowe ewolucji struktur.

Okresy oscylatorów najczęściej przyjmują wartości 2, 3, 4, 6 lub 8, choć w grze w życie znaleziono i takie, których okres wynosi prawie 150000. Dla pewnych reguł istnieje nawet oscylator o nazwie „biały rekin”, który ma okres 150000034.

Fontanna – oscylator (okres 14)

Większość liczb naturalnych może być długościami okresu oscylatora. Nie odkryto oscylatorów o okresach 19, 23, 38, oraz 41, ale jest bardzo prawdopodobne, że takowe również istnieją. Warto dodać, że jedyne znane oscylatory o okresach 34 i 51 składają się z niezależnie działających struktur o okresie 2 lub 3 i 17, na przykład oscylator o okresie 34 powstaje z oscylatorów o okresach 2 i 17 umieszczonych w określonej odległości od siebie. Dla cyklu długości 14 znamy tylko jeden oscylator (Fontanna).

Charakterystyczną cechą oscylatorów o dłuższych okresach jest podobieństwo tych o cyklu jednakowej długości (np. oscylatory długości 32 przypominają zegary z obracającą się wskazówką).

• 
  Blinker (światła uliczne)
• 
  Żabka
• 
  Krokodyl

Niestałe

Struktury niestałe zmieniają się i nigdy nie powracają do swojego stanu pierwotnego. Jest to w praktyce grupa struktur, których nie można zakwalifikować do żadnej z pozostałych kategorii, dlatego jest ich najwięcej, a ich uzyskanie nie sprawia większych trudności (losowy układ komórek wprowadzony jako warunki początkowe zwykle okazuje się być strukturą niestałą).

Niektóre struktury niestałe rozwijają się jednak w interesujący sposób. Jedną z cech, którymi opisuje się takie struktury jest stosunek liczby kroków, po których następuje stabilizacja, do liczby komórek w stadium początkowym. Stabilizacją nazywamy zamianę na konfigurację układów stabilnych, oscylatorów i statków (zwykle gliderów). Wartość ta oznaczana będzie tutaj przez L. Najważniejsze spośród najprostszych struktur niestałych:

• R-Pentomino (F-Pentomino) – chaotyczny rozwój aż do 1103 kroku, emisja kilkudziesięciu gliderów; L≈221;
• B-Heptomino – rozwój przez ponad 100 kroków aż do uzyskania zespołu struktur stabilnych; emituje glidera; L≈15;
• Pi-Heptomino – efektowny rozwój przez ponad 200 kroków aż do uzyskania charakterystycznego zespołu blinkerów (oscylatorów) i struktur stabilnych, tzw. rezultatu B-Pi; L≈30;
• Bi-Pi-Heptomino – struktura złożona z dwóch Pi-Heptomino odwróconych względem siebie do góry nogami. Efektownie rozwija się, po czym zanika po około 10 krokach czasowych;
• W-Mino – efektowny rozwój, zakończony po 50 krokach powstaniem zbioru blinkerów (oscylatorów) i struktur stabilnych; L≈6.

Najdłużej rozwijające się w struktury niezmienne nazwane są matuzalemami (nazwa pochodzi od Matuzalema). Terminem diehard (ang. die-hard - niereformowalny) natomiast określa się układ, który co prawda znika, ale dopiero po długim czasie.

• 
  Diehard – umiera po 130 krokach; ; L≈15.
• 
  Żołądź – stabilizuje się po 5206 krokach; L≈700.

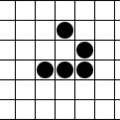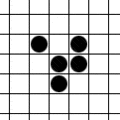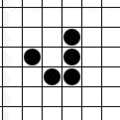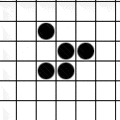
Odkryto również kilka układów nieśmiertelnych – wykazujących nieskończony wzrost. Podane poniżej ciekawe przykłady po okresie przejściowym tworzą „lokomotywy kładące bloki” (ang. „block-laying switch engine”) o okresie 288 (w wypadku ostatniego układu – dwie lokomotywy):

Nieśmiertelny układ – tylko 10 komórek – najmniejsza możliwa liczba	Nieśmiertelny układ – mieści się w kwadracie 5x5
Nieśmiertelny układ – mieści się w jednej linii

Do niedawna najmniejszy znany Ogród Edenu.

Wzór mniejszy od dotychczasowego o jedną komórkę (szare zostały usunięte, granatowe – dodane)

Ogrody Edenu formalnie są strukturami plasującymi się w kategorii niestałych, ale zostały wyróżnione ze względu na swoją szczególną właściwość. Są to bowiem układy, które nie mogą powstać w wyniku ewolucji jakiejkolwiek struktury. Jest ich bardzo niewiele, najmniejszy spośród nich składa się z około 100 komórek.

Statki (spaceships)

• 
  Glider (szybowiec)
• 
  Lot szybowca
• 
  LWSS (Dakota)
• 
  Lot Dakoty

Tzw. „statki” zwykle zmieniają się okresowo – choć okresy nie przekraczają jednak najczęściej kilkunastu kroków czasowych – ale wraz z każdym cyklem przesuwają się o stałą liczbę pól po planszy w określonym kierunku.

Najbardziej znanym przykładem takiej struktury, będącym jednocześnie niejako symbolem gry w życie, jest glider (szybowiec).

Glider

Przez długi czas po powstaniu gry w życie nie było jasne, czy istnieje jakikolwiek statek, czyli struktura, która mogłaby poruszać się w nieskończoność po planszy. Wyznaczono nawet nagrodę za jego odkrycie, w wysokości 50 dolarów. Udało się w końcu (w wyniku ewolucji R-Pentomino) odnaleźć układ, nazywany po polsku „szybowcem” (ang. glider), który przesuwa się po planszy i nigdy nie zastyga.

Układ ten stał się symbolem społeczności hakerskiej. W październiku 2003 roku Eric Raymond zaproponował szybowiec na emblemat hakerski. Został on bez większych głosów sprzeciwu zaakceptowany przez społeczność, chociaż część hakerów uważa, że społeczność nie powinna mieć godła jako takiego.

Glider jest najważniejszą strukturą gry w życie, ze względu na:

• wielkie możliwości tworzenia nowych struktur, nawet bardzo złożonych, poprzez zderzanie ich odpowiedniej ilości w odpowiednim względnym położeniu;
• olbrzymią liczbę struktur (tzw. dział) będących w stanie produkować glidery (z różnymi częstotliwościami);
• kluczowy udział w niemal każdej strukturze obrazującej pewien algorytm, np. poszukiwaniu liczb pierwszych czy generowaniu liczb pseudolosowych oraz tworzonych tylko dla samego efektu.

Glider jest oscylatorem, o okresie długości 4. Może przesuwać się wyłącznie na ukos, pod kątem 45 stopni. Nie istnieją jego modyfikacje, to znaczy, że nie istnieje taki algorytm, który pozwala na dodawanie nowych komórek tak, aby powstające struktury dalej były statkami.

Glider często powstaje samoczynnie, jako produkt reakcji, w których olbrzymia liczba komórek ewoluuje w chaotyczny sposób.

Inne statki

Dakoty: LWSS, MWSS i HWSS

Poza tym znane są także tzw. statki kosmiczne. Różnią się one od glidera kierunkiem poruszania się (pion lub poziom, a nie ukos) oraz możliwością modyfikacji – poprzez dodawanie komórek w odpowiedni sposób będziemy uzyskiwać kolejne statki. W zależności od ich wielkości nazywane są LWSS, MWSS, HWSS lub OWSS (skrótowce od Light/Medium/Heavy/Over Weight Space Ship – Lekki/Średni/Ciężki/„Nadciężki” Statek Kosmiczny). Stosuje się też do nich nazwę Dakota z liczbą określającą ich rozmiar. Jeszcze większe Dakoty nie mogą latać samodzielnie, ale mogą w towarzystwie mniejszych.

Statki

Poza tym istnieje jeszcze kilka innych statków o stosunkowo niewielkich rozmiarach (m.in. Maszyna Schicka, Rzutka). Pozostałe (kilkaset) takie struktury są duże (kilkaset żywych komórek) i trudne do tworzenia. Wymyślający je informatycy nadają im często artystyczną formę, np. ryby czy falującej wody.

Działa (guns)

Działa to oscylatory, które co jeden okres „wyrzucają” z siebie jeden statek, który odłącza się i egzystuje samodzielnie. Najwięcej dział generuje glidery, poza tym część jest zdolna do wytwarzania statków kosmicznych. Długość okresu tych struktur waha się od 30 (najprostszy Gosper Glider Gun) aż do kilkudziesięciu tysięcy kroków czasowych. Ze względu na fakt, że są to formy bardzo zaawansowane (od stu do nawet kilku tysięcy żywych komórek), ich tworzenie jest zwykle bardzo czasochłonne i wymaga praktyki.

Gosper Glider Gun

Puffery

Puffery, inaczej puffer trainy – dymiące pociągi. Struktury oscylujące (o okresie zwykle w okolicach kilkunastu kroków) oraz poruszające się po planszy, a przy tym pozostawiające za sobą cyklicznie inne struktury, które odłączają się i egzystują samodzielnie.

Najprostsze puffery (składają się one już z dwudziestu kilku żywych komórek) – zostawiają za sobą statki lub chaotyczny, stabilny pas, tzw. ruiny (debris). Bardziej złożone – oscylatory, działa czy nawet inne puffery. Powszechnie stosowaną metodą tworzenia prostych pufferów jest odpowiednie składanie MWSS-ów oraz niewielkiej struktury niestałej, jak np. B-Heptomino.

Puffery są najbardziej efektownymi strukturami gry w życie. Przykładowo, mają one możliwość przeprowadzenia algorytmu wyznaczającego liczby pierwsze. Jednocześnie, ich tworzenie jest tak trudne, że nawet doświadczeni informatycy traktują je jako wymagające nie lada poświęcenia. Wpływa na to między innymi fakt, że niektóre z tych struktur mają po 5000 komórek żywych w stadium początkowym. Do tej pory wynaleziono około setki pufferów.

Puffera, który zostawia za sobą statki, nazywamy rake'iem (ang. grabie, hulaka). Najprostszy rake składa się z 2 LWSS-ów i B-Heptomina, w skład wszystkich innych również wchodzą WSS-y. Najbardziej złożona struktura tego typu, Spider-Rake, składa się z około 1000 komórek w pierwotnym stadium. Istnieje kilkadziesiąt odkrytych rake'ów.

Breedery (ang. rozpłodnik, hodowca) natomiast to puffery o bardzo złożonym zachowaniu. Breedery pozostawiają za sobą działa lub nawet inne puffery, jednak jedynym warunkiem określającym czy dany puffer jest breederem, jest kwadratowy przyrost w czasie populacji jego żywych komórek (istnieją też działa wystrzeliwujące „hulaków” i regularne układy z brzegiem zapewniającym im rozszerzanie się). Zachowanie breederów przebiega zwykle w ten sposób: „czoło”, a więc oscylująca i produkująca nowe obiekty część puffera, wysyła w różnych kierunkach statki, które zderzając się, tworzą strukturę niezmienną. Następnie, zwykle po kilkudziesięciu krokach, wskutek zderzeń struktur niezmiennych z gliderami tworzy się działo. W takim razie, skoro co pewien okres czoło wytwarza działo, a każde z dział tworzy statek – przyrost populacji wyraża się funkcją kwadratową. Breedery są najtrudniejszymi i najbardziej skomplikowanymi (po kilka tysięcy komórek w stadium początkowym) strukturami gry w życie. Jak do tej pory, wynaleziono ich kilkanaście.

Warto jednak zwrócić uwagę, że istnieją różne złożone struktury, ale większość z nich po najdrobniejszym zakłóceniu praktycznie zawsze rozpada się, stabilizując się w sposób podobny do losowych układów. Tworzą się klocki, światła uliczne (często w formie całych skrzyżowań, jak z wypełnionego kwadratu 3 na 3), kryształy (również często w czwórkach, jak z wypełnionego kwadratu 5 na 5), bochenki, nieco łodzi, stawów i podobnych do łodzi drobnych układów stabilnych. Wylatują też szybowce. Inne migacze są rzadkością, a bardziej złożonych układów praktycznie się nie spotyka.

Przykład Breedera

Modyfikacje gry w życie

Modyfikacje reguł

Reguły, jakim podlega automat opisywane są często skrótowo w następujący sposób:

• przed ukośnikiem umieszcza się te liczby komórek w sąsiedztwie, dla których żywe komórki przeżywają (dla reguły Conwaya będzie to 23);
• następnie umieszcza się ukośnik: /;
• po ukośniku umieszcza się te liczby komórek w sąsiedztwie, dla których martwe komórki ożywają (dla reguły Conwaya będzie to 3);

Reguły Conwaya można więc zapisać: 23/3, a reguły Trzy Cztery: 34/34.

Inny zapis reguł, stosowany np. przez program Golly, polega na wypisaniu po literze B liczb sąsiadów dającej narodziny, a następnie po ukośniku i literze S liczb sąsiadów dającej przeżycie. Reguły Conwaya zapisuje się wtedy jako: B3/S23, a reguły Trzy Cztery jako B34/S34.

Chaotyczne diamenty – Diamoeba (5678/35678)

Eksplodujący chaos – Seeds (/2)

Gra w życie – reguły Conwaya (23/3)

Pedały – reguły 3/3

Modyfikacji gry w życie jest zbyt wiele (2¹⁸ = 262144), by pomieścić je tu wszystkie. Tabela zawiera reguły dołączone do programu Mirek's Cellebration, te wspomniane przez Wolframa oraz kilka innych.

Reguła	Nazwa	Opis
/2	Seeds (nasiona)	Wzrost intensywny, chaotyczny
/234	Serwety	Przypomina koronki, serwety
012345678/1		Wolfram – 7(e)
012345678/3	Płatki, Życie bez śmierci	Wzory przypominają drabiny. [3]
012345678/378		Wolfram – 9(a)
01356/13456		Wolfram – 7(d)
018/018		Wolfram
0238/123567		Wolfram – 13(f); klasa 3
03456/34		Wolfram – 7(g)
045/0578		Wolfram – 7(i)
0468/236		Wolfram – 7(a), 13(g); klasa 3
1/1	Narośl	Opracowany przez Kellie Evans; tworzy interesujące formy, startuje nawet od pojedynczej komórki.
12345/3	Labirynt	Tworzy wzory przypominające labirynty.
12456/0578		Wolfram – 7(h)
125/36	2x2	Ma dużo oscylatorów i statków
135/135		Wolfram – 13(h); klasa 3
1357/1357	Replikator	Automat replikujący Edwarda Fredkina, każda struktura jest z czasem zastępowana przez jej kilka kopii
1358/357	Ameba	Dobrze zbalansowana między życiem a śmiercią, ma statki
23/3	Gra w życia Conwaya	Bardzo złożone zachowania (odkryte kilkadziesiąt tysięcy sensownych struktur)
23/36	HighLife	Podobne do Gry w życie (część jej struktur działa w HighLife), w dodatku struktura samoreplikująca
234/3		Wolfram – 9(b), 13(b); klasa 2. ma statki
2345/45678	Miasta otoczone murem	Tworzy aktywne centra otoczone statycznymi ścianami
2346/367		Wolfram – 9(c). ma statki
235678/3678	Plamy	Struktury szybko się stabilizują, o dziwo znacznie różni się od poprzedniej reguły
235678/378	Koagulacje	Wzory rozszerzają się, w przeciwieństwie do plam
238/357	Pseudożycie	Ewolucja przypomina 23/3, ale mało który wzór z gry w życie działa pod tymi regułami
245/368	Ruch	Losowe struktury zwykle się stabilizują, ale wiele statków występuje naturalnie i często się pojawia. Najczęściej pojawiają się struktury stabilne, okresowe z okresem 2 lub 4, statek o okresie 7 i „dymiący pociąg” o okresie 170.
27/257		Wolfram – 7(b); ma statki
34/34	Trzy Cztery	Początkowo sądzono, że ma ona tendencje do stabilizacji, ale dzięki symulacji komputerowej okazało się, że większe wzory eksplodują. Dużo małych oscylatorów i statki.
34678/3678	Dzień i Noc	Dużo wzorów o złożonym zachowaniu. Wzory można odwracać – uczynić wszystkie żywe komórki martwymi i na odwrót, a będzie on działał identycznie.
4567/345	Asymilacja	Tworzy statystyczne struktury przypominające diament, wnętrza kryształów częściowo wypełnione
45678/137		Wolfram – 7(f)
45678/3	Koral	Wzory rosną powoli, tworzą struktury przypominające rafę koralową.
5/345	Długie życie	Reguła opracowana przez Andrew Trevorrowa, bardzo łatwo można spotkać oscylatory o długim okresie.
5678/35678	Diameba	Tworzy wielkie zwarte struktury z chaotycznie oscylującymi granicami. Zajmował się nią Dean Hickerson, który też znalazł wzory, których przyrost jest kwadratowy.

Z elementem /0 wszystkie komórki z dala od struktury ożywają. Poza tym istnieje kilka reguł, które ograniczają istnienie statków:

• wszystkie reguły, które zawierają element /1, np. 1/1 lub 01356/13456 będą miały charakter eksplozji dla każdego wzoru początkowego. Dla każdego kroku czasowego komórka (x,y), gdzie x i y to minimalne współrzędne żywej komórki, komórka (x-1,y-1) ma tylko 1 żywego sąsiada, więc ożyje.
• Elementy nie posiadające /2 ani /3 nie mogą się rozszerzać.
• Z 0123/ żadna struktura nie może cofać swojego brzegu.
• Bez żadnego z 012345/245 żaden wzór nie może uciec poza „diament”, który na początku go ogranicza.
• Z 234567/ i bez /2 żaden wzór nie może opuścić początkowego „diamentu” bez utworzenia nieśmiertelnego trójkąta.
• Z 123456/, 1234/345 lub 12345/34 połączone struktury nie mogą się kurczyć.

Łatwo też stwierdzić, że w regułach z /2 struktura mająca na brzegu dwie sąsiadujące żywe komórki przekształci się w następnym kroku w strukturę, w której dwie komórki są na brzegu, ale dalej. Większość struktur rozszerza się więc w nieskończoność z prędkością światła (o jedną komórkę na krok).

Modyfikacje kształtu komórek

Oprócz powszechnie przyjętego podziału płaszczyzny na kwadraty można zastosować także sześciokąt (siatka heksagonalna). Najczęściej stosowaną regułą jest 3/24, jednak nie znaleziono struktur tak interesujących jak w oryginale.

Modyfikacje kolorystyczne

Nie zmieniając reguł automatu, możemy zabarwić część komórek, co da ciekawszy efekt, nie wpłynie jednak na kształt generowanych struktur.

Immigration

Żabka w Immigration

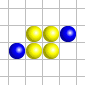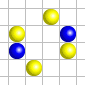
• Dla żywych komórek dostępne są dwa kolory – zwykle czerwony i żółty. Dla martwych sytuacja się nie zmienia względem oryginału.
• Definiując warunki początkowe każdej z komórek przypisujemy jeden kolor. Na każdy z kolorów powinna być zabarwiona przynajmniej jedna komórka, w przeciwnym razie uzyskamy zwykłą grę w życie.
• Nowo powstające komórki przyjmują taki kolor, jaki ma większość z ich 3 żywych sąsiadów.
• Kolory żywych komórek nie zmieniają się w trakcie gry.

QuadLife

Glider gun w QuadLife

• Dla żywych komórek dostępne są aż cztery kolory – zwykle czerwony, żółty, zielony i niebieski. Dla martwych sytuacja się nie zmienia względem oryginału.
• Definiując warunki początkowe każdej z komórek przypisujemy jeden kolor. Na przynajmniej dwa spośród kolorów powinna być zabarwiona przynajmniej jedna komórka, przeciwnym razie uzyskamy zwykłą grę w życie.
• Nowo powstające komórki przyjmują taki kolor, jaki ma większość z ich 3 żywych sąsiadów; jeżeli ma po jednym sąsiedzie z każdego koloru, przyjmuje pozostały kolor.
• Kolory żywych komórek nie zmieniają się w trakcie gry.

Darwinia

Gra w życie pojawiła się jako jedno z intr do gry komputerowej Darwinia

• Każda komórka może pozostać żywa najwyżej przez 50 cykli, później umiera.
• Plansza ma skończony rozmiar, poza którym komórki nie mogą się rodzić.
• Poza tym stosowane są klasyczne zasady Conwaya 23/3.
• Warunki początkowe zostały dobrane tak, że kończą się śmiercią wszystkich komórek. Istnieją jednak obiekty żyjące wiecznie, jak chociażby Krokodyl.

Charakterystyka automatu komórkowego Gra w życie

Stephen Wolfram, który podzielił automaty komórkowe na cztery różne klasy, biorąc pod uwagę efekty jakie one wywołują, przyporządkował grę w życie do klasy czwartej, charakteryzującej się tym, że nie prowadzi ona ani do globalnego porządku, ani do globalnego chaosu. Chris Langton, twórca innego popularnego automatu komórkowego, znanego jako mrówka Langtona wykazał w roku 1991, że proponowana przez Wolframa klasa czwarta, znajduje się pomiędzy klasą zachowań chaotycznych (klasa II) i struktur okresowych (klasa III).

Gra w życie może wykonywać obliczenia i jest równoważna maszynie Turinga. Przykładem uniwersalności gry w życie może być implementacja języka Lisp.

Zobacz też

• DigiHive
• sztuczne życie
• Tierra

Bibliografia

• Conway's Game of Life
• What is the Game of Life?
• PeterP. Coveney PeterP., RogerR. Highfield RogerR., Granice złożoności. Poszukiwania porządku w chaotycznym świecie, Warszawa: Prószyński i S-ka, 2007, ISBN 83-7180-083-5 .

Linki zewnętrzne

• Obszerna strona dotycząca Gry w życie, zawierająca aplet do generacji automatów komórkowych. (ang.)
• Strona dotycząca gry w życie z programami i wzorami. (ang.)
• Gra w życie działająca na stronie internetowej
• Strona Davida Bella, kolekcja wzorów gry w życie (szczególnie statki).
• Gra w życie wersja gry w życie w technologii Flash
• Eric W.E.W. Weisstein Eric W.E.W., Gra w życie, [w:] MathWorld, Wolfram Research  (ang.).
• LifeWiki – Encyklopedia wiki poświęcona grze w życie
• Conway's game of life implementation. (Silverlight). andrei1606.brinkster.net. [zarchiwizowane z tego adresu (2014-03-18)]. (ang.)
• Film W krainie matematyki: Gra w życie, reż. Denis van Waerebeke (10 min) w Arte.tv